3.4. Уравнение Эйлера.

Это уравнение позволяет находить экстремаль.

Получим уравнение Эйлера.

Пусть задан функционал более общего вида

Требуется найти функцию, которая доставляет минимум этому функционалу.

На рис. 3.4 показаны моменты времени t₀ , t₁ , и отвечающие им функции y₀ , y₁ . Нужно найти уравнение такой линии 1, на которой функционал был бы экстремальным.

Предположим, что уравнение линии дается функцией

Обозначим производную dy / dt как – для удобства записи.

y(t)

y₁

2

1

y₀

t₀ t₁ t

Рис. 3.4. Разные функции, имеющие общие точки.

Возьмем вариацию этой функции и определим приращение функционала:

Потребуем, чтобы варьируемая функция проходила через точки (t₀ , y₀) и (t₁ , y₁)  точки, принадлежащие экстремали. Значит, вариации и .

Разложим проварьированную функцию в ряд Тейлора:

где - остаток порядка малости больше двух.

Рассматривается только линейная часть приращения – это первый член разложения в фигурных скобках. Остальными членами надо пренебречь. Тогда для вариации фонкционала получим выражение

Проинтегрируем по частям второе слагаемое.

(Формула ).

Первый член разности равен нулю, т.к. по условию задачи. Тогда вариация будет

или

Интеграл равен нулю когда подынтегральная функция равна нулю. Эта функция есть уравнение Эйлера:

Пример. Найти уравнение кривой, соответствующей минимуму функционала

Начальные условия: t = 0, y = y₀ .

Находим:

Подставляя в (3.18) , получаем уравнение Эйлера для данного примера:

Решение этого уравнения дает экстремаль. Это будет функция Со временем второе слагаемое обращается в нуль. Применяя начальные условия, получаем:

3.5. Задачи вариационного исчисления

Задачи, в которых граничные точки заданы (см. рис. 3.4) , называются задачами с закрепленными концами. Один конец экстремали в начальной точке, другой в конечной.

Задачи, в которых граничные точки не закреплены, а находятся на некоторых линиях или поверхностях пространства координат, называются задачами с незакрепленными концами. Если экстремаль должна проходить между поверхностями, никаких определенных конечных точек не задается. Они могут находиться в любой точке поверхности. Поэтому, для определения постоянных интегрирования нужно иметь некоторые условия. Допустим имеются две поверхности (t, у) и (t, у). Начальные и конечные точки находятся из соотношений, которые называются условиями трансверсальности:

Условия трансверсальности дают возможность определить постоянные интегрирования в уравнении Эйлера и тем самым получить конкретное решение.

Другой класс задач – задачи на условный экстремум.

Задается функционал

И дополнительные уравнения, выражающие зависимость между собой переменных задачи. Зависимость выражается уравнениями связи:

Такие задачи решаются путем сведения их к безусловному экстремуму. Для этого вводится новая функция

Величины называются множителями Лагранжа. Для функции L решают систему уравнений Эйлера

Которая дополняется заданными уравнениями связи и граничными условиями. Получается n уравнений Эйлера, m уравнений связи, граничные условия для определения неизвестных

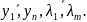
Пример. Дано уравнение объекта

Найти оптимальное управление. Критерий оптимальности

На процесс наложено ограничение

Граничные условия: t = 0, t = T

Перейдем к переменным состояния:

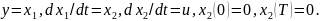
Если ограничивающее условие задано определенным интегралом, то оптимальное решение ищется с помощью уравнения Лагранжа

и уравнение Эйлера

Находим:

Подстановкой в (3.23) получаем уравнение

После интегрирования, имея ввиду, что dx₂ / dt = u , получаем закон управления:

Повторяем интегрирование и получаем оптимальную скорость процесса:

В уравнении (3.24) имеется три неизвестных . Их следует определить, используя граничные условия (3.21) и ограничение (3.22) . Подстановка t = 0 x₂ = 0 дает: . Остается

Следующая подстановка, t = T , x₂ = 0 позволяет получить:

Проинтегрируем уравнение (3.24), имея ввиду, что

и получим:

Решая совместно (3.25) и (3.26), находим неизвестные и :

Подставляя в закон управления, окончательно получаем:

Вначале, пока 0  t  T/2 , управление положительное. При t = T/2 функция имеет знак и при t  T/2 управление отрицательное. В момент t = T управление снимается.