6. Уравнение Шредингера

Волновая функция является функцией координат и времени и может быть определена решением временного уравнения Шредингера, установленного в 1926 году:

Здесь U – потенциальная энергия частицы массой m, а Δ – оператор Лапласа:

Для стационарного силового поля потенциальная энергия не зависит от времени, поэтому

Тогда стационарное уравнение Шредингера или в дальнейшем просто уравнение Шредингера:

Здесь E – полная энергия частицы.

7. Частица в потенциальной яме

Частица находится в одномерной потенциальной яме длиной L с бесконечно высокими стенками:

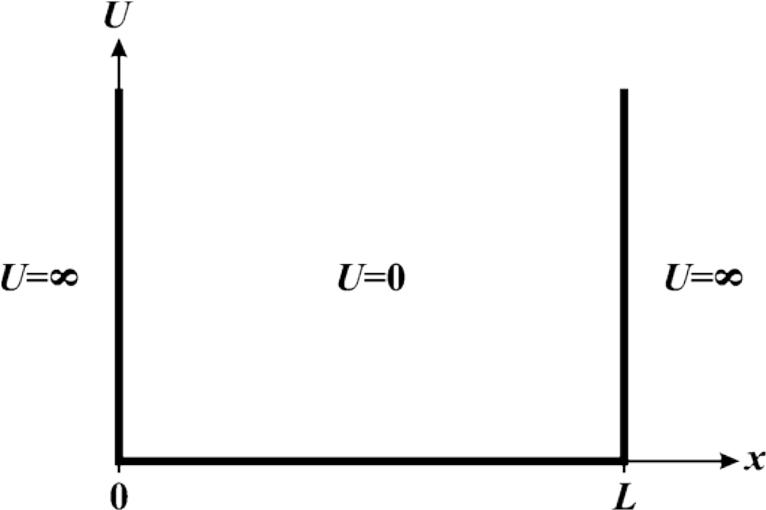
Стационарное уравнение Шредингера может быть тогда записано, как

За пределами ямы вероятность нахождения частицы равна нулю, поскольку её полной энергии недостаточно для преодоления стенок бесконечно высокой энергии. Тогда за пределами ямы и волновая функция равна нулю.

Из условия непрерывности волновой функции следует, что и на границах ямы её значение равно нулю:

Это и есть условие, которому должно удовлетворять решение уравнения Шредингера. Соответственно, для частицы внутри ямы уравнение выглядит, как

Введя обозначение

можем записать

Общее решение подобных уравнений можно представить в виде

где A и α – произвольные постоянные.

в другом случае

откуда

где n=1,2,3,… – целое число.

Учитывая, что до этого мы приняли

Получаем

где вновь n=1,2,3,… Таким образом, спектр значений энергии частицы в потенциальной яме является дискретным, а число n определяет номер её энергетического уровня.

Определим теперь аналитический вид волновых функций частицы, соответствующих каждому из энергетических уровней.

Принимая во внимание полученное условие

перепишем волновую функцию

в виде

Для определения коэффициента A воспользуемся условием нормировки

На концах интеграла подынтегральная функция равна нулю, поэтому значение интеграла равно произведению среднего значения квадрата синуса (а оно равно ½) на ширину ямы L. Тогда

Следовательно, волновую функцию уровня n можно полностью представить, как

а распределение плотности вероятности ψ² нахождения частицы на данном уровне, как

На графиках представлены первые четыре волновые функции и распределения плотности вероятности нахождения частицы в потенциальной яме:

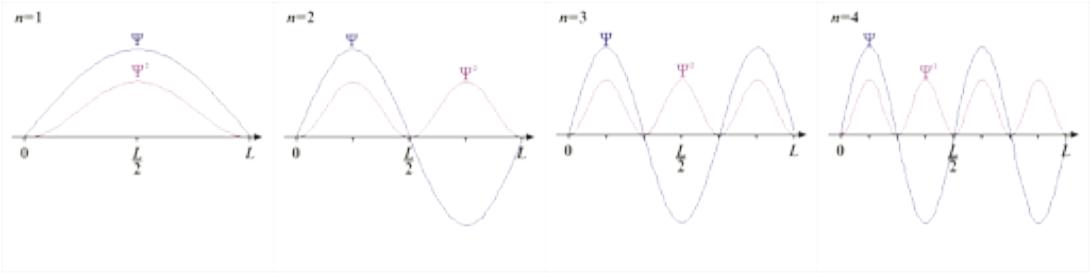
8. Гармонический осциллятор

В квантовой теории понятие силы теряет смысл, поэтому квантовый гармонический осциллятор следует определять как поведение частицы массы m с потенциальной энергией U(x) такой же, как у классического осциллятора:

где k – константа.

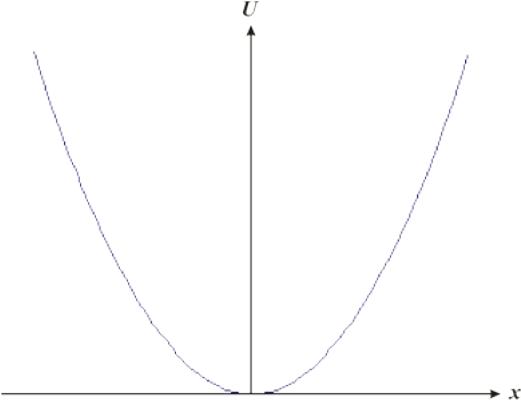
Согласно классической механике гармонический осциллятор совершает колебания с частотой:

Тогда потенциальную энергию можно записать в виде

а уравнение Шредингера в виде

Не вдаваясь в детали решения, отметим, что энергия осциллятора квантуется и определяется выражением

где n=0,1,2,…