
Шейпак А.А. Гидравлика и гидропневмопривод (часть 2)
.pdf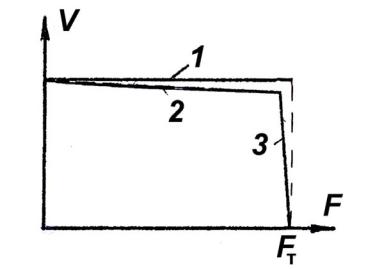
Особенностью гидропривода, схема которого приведена на рис. 7.15,а, является то, что давление на выходе насоса зависит от нагрузки на выходном звене (на штоке гидроцилиндра), а клапан 1 – предохранительный.
В гидроприводе, схема которого приведена на рис. 7.15,а, давление на выходе насоса поддерживается постоянным при помощи переливного клапана 1.
На рис. 7.16 приведена нагрузочная характеристика гидропривода с дроссельным регулированием скорости, в котором используется один из вариантов системы стабилизации, рассмотренный выше.
Рис. 7.16. Нагрузочная характеристика гидропривода с системой стабилизации скорости
На графике для сравнения приведены идеальная нагрузочная характеристика 1, построенная с учетом принятых допущений (она имеет вид горизонтальной прямой, то есть имеет «абсолютную жесткость»), и реальная характеристика, которая при этом имеет вид ломаной линии. Реальная характеристика состоит из прямой 2, наклон которой определяется жесткостью пружины соответствующего клапана в дроссельном регуляторе расхода, и прямой 3, характеризующей работу гидропривода в режиме перегрузки (сработал предохранительный клапан).
7.4. Сравнение различных способов регулирования
Сравнение различных способов регулирования проводится по нагрузочным и энергетическим характеристикам, построенным в относительных величинах.
211
7.4.1. Сравнение по нагрузочным характеристикам
Под нагрузочной характеристикой регулируемого гидропривода в относительных величинах понимается графическая зависимость относи-
тельной скорости V выходного звена гидропривода от относительной нагрузки F на нем при постоянном значении параметра регулирования.
Под относительной нагрузкой F на выходном звене гидропривода понимается величина, равная отношению значения преодолеваемого усилия F к максимальному (тормозному Fт).
При построении нагрузочных характеристик под относительной скоростью V движения выходного звена гидропривода принята величина, равная отношению действительной скорости V при данной нагрузке к максимальному значению этой скорости Vmax при том же значении параметра регулирования.
Для гидропривода с дроссельным регулированием при параллельном включении дросселя (см. параграф 7.2.1), используя выражение (7.6), оп-
ределим относительную скорость: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 F |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Q |
−µS |
др |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
µSдр |
|
|
|
|
|
|
|
|
V |
|
Sп |
|
|
|
|
ρ Sп |
|
|
|
2 Fт F |
|
||||||
V = |
= |
|
Qн |
|
|
=1 |
− |
=1− F . (7.15) |
|||||||||||||
V |
|
|
|
|
|
|
|
|
|
Q |
ρ S |
п |
F |
||||||||
|
|
|
max |
|
|
|
|
|
Sп |
|
|
|
|
|
|
н |
|
т |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь учитывается, что при нагрузке на выходном звене гидропривода равном тормозному усилию Fт действительная скорость V движения выходного звена равна нулю. При этом вся подача насоса через регулируемый дроссель сливается в бак, т.е.
Q = µS |
2 Fт . |
н |
др ρ Sп |
Для гидроприводов с дроссельным и объемно-дроссельным регулированием при последовательном включении дросселя (см. параграфы 7.2.2 и 7.2.4), используя выражение (7.8), найдем –
V = V
Vmax
|
|
Sдр |
2 |
|
|
|
|
F |
|
||
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Sп |
|
|
|
pн − |
|
|
|
|||
= |
|
|
ρ |
|
|
Sп |
= |
||||
|
|
Sдр |
|
|
2 |
|
|
|
|||
|
|
µ |
|
|
pн |
|
|
|
|||
|
|
Sп |
|
|
ρ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
1 |
− |
S |
F |
= 1− |
F |
= |
1− F . (7.16) |
|
|
p |
|
F |
|
|
|
|
|
|
п н |
|
т |
|
|
В данном случае под тормозным усилием Fт понимается нагрузка на выходном звене гидропривода, при котором перепад давления на гидродросселе равен нулю, т.е. Fт = pнSп.
Для гидроприводов со стабилизацией скорости, в которых используются дроссельные регуляторы расхода (см. параграф 7.3), и с объемным регулированием (см. параграф 7.2.3) вследствие того, что скорость движе-
212
ния выходного звена в этих гидроприводах не зависит от нагрузки на нем во всем диапазоне ее изменения, величина относительной скорости такова:
V =1. (7.17)
Используя полученные зависимости (7.15), (7.16) и (7.17), на рис. 7.17 для сравнения построены следующие нагрузочные характеристики:
1– для гидропривода с дроссельным регулированием при параллельном включении дросселя,
2– для гидроприводов с дроссельным и объемно-дроссельным регулированием при последовательном включении дросселя,
3– для гидроприводов со стабилизацией скорости и с объемным регулированием скорости.
Сравнение этих зависимостей с точки зрения «жесткости» нагрузочной характеристики указывает на неоспоримые преимущества гидроприводов со стабилизацией скорости, в которых используются дроссельные регуляторы расхода, и гидропривода с объемным регулированием скорости.
Рис. 7.17. Нагрузочные характеристики регулируемых гидроприводов, построенные в относительных величинах
7.4.2. Сравнение по энергетическим характеристикам
Под энергетической характеристикой регулируемого гидропривода в относительных величинах понимается графическая зависимость КПД системы регулирования гидропривода от относительной скорости его выходного звена при постоянном значении относительной нагрузки на нем.
В данном случае под относительной скоростью V движения выходного звена понимается величина, равная отношению текущего значения скорости V при заданной нагрузке к максимально возможному значению этой скорости Vmax при той же нагрузке.
213

Для гидропривода с дроссельным регулированием при параллельном включении дросселя, учитывая выражение (7.6) и то обстоятельство, что Vmax получается при Sдр = 0 , относительная скорость V равна:
|
|
|
|
|
1 |
|
|
|
|
|
2 F |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Q |
−µS |
др |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
µSдр |
|
|
|
|
|
|
|
|
V |
|
Sп |
|
|
|
|
ρ Sп |
|
|
2 F |
|
|
||||||
V = |
= |
|
Qн |
|
|
=1 |
− |
. |
(7.18) |
||||||||||||
V |
|
|
|
|
|
|
|
|
|
Q |
ρ S |
п |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
max |
|
|
|
|
|
Sп |
|
|
|
|
|
|
н |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для гидроприводов с дроссельным и объемно-дроссельным регулированием при последовательном включении дросселя, учитывая выражение (7.8), соответственно получим:
V = V
Vmax
µSдр
=Sп 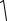
µSдрmax
Sп
2 |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
pн − |
|
|
|
|
|
|
|
Sдр |
|
|
|
ρ |
|
|
Sп |
= |
|
. |
(7.19) |
|||||
|
|
|
|
|
|
|
|
S |
|
|||
|
2 |
|
|
|
F |
|
дрmax |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
pн |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ρ |
|
|
Sп |
|
|
|
|
||||
Такой же результат получается и для гидропривода со стабилизацией скорости, в котором используется дроссельный регулятор расхода при последовательном включении дросселя (см. параграф 7.3).
Для гидропривода вращательного движения с объемным регулированием скорости в схеме с регулируемым насосом и нерегулируемым гидро-
мотором относительную скорость вычисляем по формуле: |
|
|||||||||||
|
|
|
|
|
|
Wнmax |
eнnн |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
nг |
= |
|
|
Wг |
= eн . |
(7.20) |
|||
V |
= |
|||||||||||
|
|
Wнmax |
||||||||||
|
|
|
nгmax |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
nн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Wг |
|
|
|||
Под КПД системы регулирования понимается КПД гидропривода, учитывающий потери энергии только в гидравлических элементах, обеспечивающих регулирование скорости выходного звена. Следовательно, при определении соответствующего КПД системы регулирования остаются в силе те допущения, которые делались при выводе законов регулирования (см. параграф 7.2).
В общем случае КПД системы регулирования определяется как отношение полезной мощности, развиваемой на выходном валу гидропривода, к мощности, потребляемой гидроприводом, без учета потерь в гидролиниях, направляющих гидрораспределителях и гидромашинах, т.е.
η = Nвых .
Nвх
Для гидропривода с дроссельным регулированием при параллельном включении дросселя (см. параграф 7.2.1), учитывая принятые допущения Nвых = FV , Nвх = pнQн, F = pнSп и используя выражение (7.6), значение КПД системы регулирования получаем в виде:
214
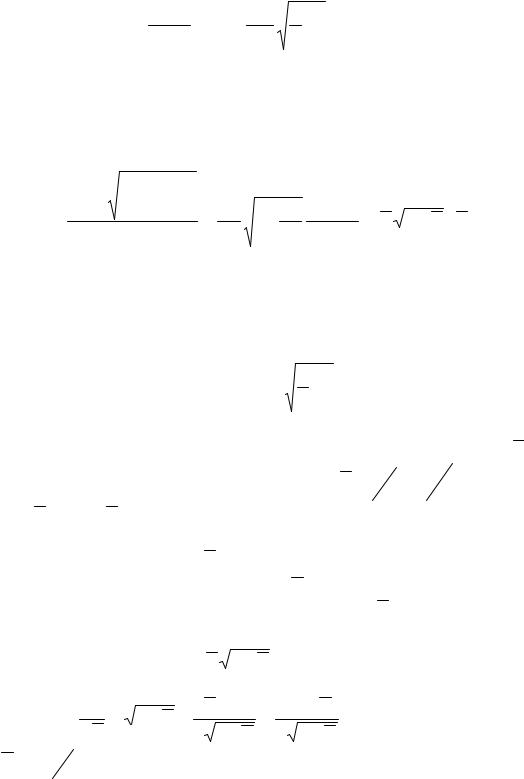
|
FV |
|
|
Sдр 2 |
|
η = |
p Q |
=1−µ |
Q |
ρ pн . |
|
|
н н |
|
|
н |
|
Сравнив полученную формулу с выражением (7.18), получим: |
|||||
|
|
|
|
|
(7.21) |
|
|
η =V |
|
||
Для гидропривода с дроссельным регулированием при последовательном включении дросселя на входе в гидродвигатель (см. параграф 7.2.2), обозначив p = F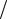 Sп , с учетом (7.19) можно записать:
Sп , с учетом (7.19) можно записать:
|
|
|
|
|
µS |
|
2 |
(p |
|
− p) |
|
|
|
|
|
|
|
|
|
|
FV |
|
p |
др ρ |
н |
p |
1 |
|
p |
|
Sдр |
= F 1 |
− F V . (7.22) |
||||||
η = |
= |
|
|
= |
− |
|
|||||||||||||
p Q |
p |
н |
|
|
Q |
|
p |
н |
p |
S |
дрmax |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
н н |
|
|
|
|
|
н |
|
|
|
|
|
н |
|
|
|
|||
При получении формулы (7.22) принято, что подача нерегулируемого насоса Qн в правильно спроектированном гидроприводе должна обеспечивать максимально возможную скорость движения выходного звена, т.е. в рассматриваемом случае при максимальном открытии регулируемого дросселя и усилии на выходном звене, равном нулю
Q |
=V |
S |
|
= µS |
2 p |
|
. |
(7.23) |
н |
max |
|
п |
|
дрmax ρ |
н |
|
|
Из формулы (7.22) видно, что КПД системы регулирования гидропривода в данном случае есть функция не только относительной скорости V
его выходного звена, но и относительной нагрузки F = F Fт = p pн на нем.
Причем при F = 0 и F =1 КПД системы регулирования становится равным нулю. Очевидно, что при этом существует некоторое оптимальное значение относительной нагрузки Fопт , при котором КПД системы регули-
рования при данной относительной скорости V максимально. Определим это оптимальное значение нагрузки Fопт на выходном
звене гидропривода. Для этого исследуем на максимум функцию:
|
|
|
|
α = F 1− F . |
(7.24) |
|
Приравняв к нулю производную от этой функции |
||||||
|
|
|
dα |
= 1− F + F (−1) |
= 2 −3F |
= 0 , |
|
= 2 |
|
dF |
2 1− F |
2 1− F |
|
получим F |
3 |
. |
|
|
|
|
опт |
|
|
|
|
|
|
Таким образом, зависимость максимальных значений КПД системы регулирования гидропривода с дроссельным регулированием при последо-
|
|
|
|
|
после под- |
вательном включении дросселя от относительной скорости V |
|||||
становки в формулу (7.22) полученного значения |
|
опт приобретает вид: |
|||
F |
|||||
|
|
. |
(7.25) |
||
η 0,385 V |
|||||
КПД системы регулирования для гидропривода со стабилизацией скорости, в котором используется дроссельный регулятор расхода на основе
215

переливного клапана (рис. 7.15,а), при последовательном включении дросселя определим, учитывая постоянство перепада давления ∆pдр на этом
дросселе, равенство pн = ∆pдр + F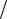 Sп и соотношение (7.19), а также при-
Sп и соотношение (7.19), а также при-
нимая подачу насоса равной расходу, обеспечивающему максимальную скорость движения выходного звена гидропривода, в следующем виде:
|
|
|
|
|
|
|
|
|
|
µSдр |
2 |
∆pдр |
|
|
|
|
|
|
|
|
||||
|
FV |
|
|
|
|
F |
|
|
|
ρ |
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
η = |
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
V . |
(7.26) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p Q |
|
|
|
|
|
F |
|
|
|
2 |
|
|
|
∆pдрSп |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
н н |
|
S |
|
∆p |
др |
+ |
|
|
µS |
др |
|
|
|
∆p |
др |
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
п |
|
|
|
|
|
max |
|
ρ |
|
|
|
F |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Sп |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, на основании полученной формулы (7.26) можно заключить, что КПД системы регулирования рассматриваемого гидропривода при значительной по величине нагрузки, преодолеваемой выходным звеном гидропривода, изменяется в функции относительной скорости практически так же, как и в случае для гидропривода с параллельным включением дросселя (7.21).
КПД системы регулирования для гидропривода со стабилизацией скорости, в котором используется дроссельный регулятор расхода на основе редукционного клапана (рис. 7.15,б), при последовательном включении дросселя определим, учитывая постоянство перепада давления ∆pдр на
этом дросселе, постоянства давления питания pн = Fт 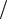 Sп и соотношение
Sп и соотношение
(7.19), а также принимая подачу насоса равной расходу, обеспечивающему максимальную скорость движения выходного звена гидропривода, в следующем виде:
|
|
|
|
µSдр |
2 |
∆pдр |
|
||
|
FV |
|
F |
ρ |
|
||||
η = |
= |
|
|
|
= F V . |
(7.27) |
|||
|
|
|
|||||||
p Q |
F |
|
|
2 |
|||||
|
|
|
|
|
|
|
|||
|
н н |
|
т |
µSдр |
|
|
|
∆pдр |
|
|
|
max |
|
ρ |
|
||||
|
|
|
|
|
|
|
|
||
Анализ полученной формулы (7.27) позволяет заключить, что на величину КПД системы регулирования рассматриваемого гидропривода оказывают влияние оба фактора: относительная величина нагрузки F , преодолеваемая выходным звеном гидропривода, и его относительная скорость V .
КПД системы регулирования для гидропривода вращательного движения с объемным регулированием (рис. 7.9), учитывая принятые допущения и считая Qн = Qг и pн = ∆pг , получим:
η = |
M гωг |
= |
Qг∆pг |
=1. |
(7.28) |
||||
|
|
||||||||
|
M |
н |
ω |
н |
|
Q p |
н |
|
|
|
|
|
|
н |
|
||||
Значит, что при объемном регулировании потери энергии отсутствуют. Этот результат является следствием допущения о том, что во всем диапазоне регулирования рабочего объема гидромашины ее КПД остается
216
равным единице. Реально, в соответствии с теорией регулируемых роторных гидромашин, их КПД есть функция параметра регулирования рабочего объема. Причем КПД регулируемого насоса принимает максимальное значение при ен = 1 и становится равным нулю при ен = 0.
КПД системы регулирования гидропривода с объемно-дроссельным регулированием при последовательном включении дросселя на выходе из гидродвигателя (рис. 7.12), учитывая то, что pн = Fт 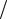 Sп и Qн = Qдр =VSп,
Sп и Qн = Qдр =VSп,
можно определить в виде: |
|
|
|
|
FQдр |
|
|
|
|
||
|
FV |
|
|
|
|
|
|
||||
η = |
|
= |
= F . |
(7.29) |
|||||||
p |
Q |
p |
S Q |
||||||||
|
|
|
|
|
|
||||||
|
н |
|
н |
|
н |
п н |
|
|
|
|
|
Таким образом, формула (7.29), полученная в соответствии с принятыми допущениями, показывает, что в гидроприводе с объемнодроссельным регулированием скорости КПД системы регулирования не зависит от относительной скорости V выходного звена, а определяется только относительной нагрузкой F на нем и так же, как и F , без учета потерь в гидромашинах изменяется от нуля до единицы.
На практике важно знать КПД системы регулирования для работы гидропривода в режиме передачи им максимальной полезной мощности. Определим значение относительной нагрузки F на выходном звене гидропривода.
Полезная мощность, развиваемая гидроприводом (рис. 7.12) на его выходном звене при данной нагрузке, равна
|
|
|
|
|
|
|
|
|
Sдр |
2 |
|
|
F |
|
|
|
|
|
Nпол = FV = F µ |
|
|
|
|
|
|
||||
|
|
|
|
Sп |
pн − |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
ρ |
|
|
Sп |
||
|
Принимая во внимание, что pн = Fт |
Sп , умножив и разделив выраже- |
||||||||||||
ние на Fт, получим |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
F FтµSдр |
2 |
|
|
F |
|
|
|
|
||
|
|
Nпол = F |
S |
|
|
|
|
|
|
= F |
1− F A, |
|||
|
|
п |
ρ pн 1− p S |
|
||||||||||
|
|
|
|
т |
|
|
|
|
н |
п |
|
|
|
|
где |
A = µSдр |
2 |
3 |
– постоянная величина. |
|
|
|
|
||||||
ρ |
pн |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Максимальная |
передаваемая |
полезная |
мощность гидроприводом в |
||||||||||
данном случае достигается при максимальном значением функции α из формулы (7.24), которая, как было показано выше, принимает максимальное значение при относительной нагрузке на выходном звене гидроприво-
да F = 23 .
Следовательно, в этом режиме работы гидропривода с объемнодроссельным регулированием при последовательном включении дросселя КПД его системы регулирования равен
η 0,667 . (7.30)
217
На практике в этом случае необходимо учитывать приведенные выше оговорки о влиянии на КПД регулируемого насоса величины его параметра регулирования.
На рис. 7.18 для сравнения приведены графики энергетических характеристик гидроприводов, построенные в соответствии с формулами (7.21), (7.25), (7.26), (7.27), (7.28) и (7.30) при относительной нагрузке F на вы-
ходном звене гидропривода, равной 2/3.
Рис. 7.18. Энергетические характеристики регулируемых гидроприводов, построенные в относительных величинах
На графике сплошными линиями нанесены зависимости, полученные в соответствии с принятыми допущениями, а пунктирными – ориентировочный вид зависимостей для гидроприводов с объемным и объемно-дрос- сельным регулированием, построенные с учетом зависимости КПД регулируемого насоса от его параметра регулирования.
На рис. 7.18 под следующими номерами приведены энергетические характеристики:
1 – для гидропривода с дроссельным регулированием при параллельном включении дросселя (рис. 7.3);
2 – для гидропривода с дроссельным регулированием при последовательном включении дросселя (рис. 7.5);
3– для гидропривода (рис. 7.15,а) со стабилизацией скорости, в котором используется дроссельный регулятор расхода на основе переливного клапана при последовательном включении дросселя;
4– для гидропривода (рис. 7.15,б) со стабилизацией скорости, в котором используется дроссельный регулятор расхода на основе редукционного клапана при последовательном включении дросселя;
218
5– для гидропривода с объемным регулированием (рис. 7.9);
6– для гидропривода с объемным регулированием (рис. 7.9) с учетом зависимости КПД регулируемого насоса от его параметра регулирования;
7– для гидропривода с объемно-дроссельным регулированием при последовательном включении дросселя на выходе из гидродвигателя (рис. 7.12);
8– для гидропривода с объемно-дроссельным регулированием при последовательном включении дросселя на выходе из гидродвигателя (рис. 7.12) с учетом зависимости КПД регулируемого насоса от его параметра регулирования.
Сравнение гидроприводов по приведенным энергетическим характеристикам указывает на неоспоримые преимущества гидропривода с объемным регулированием скорости. Однако при этом следует помнить, что стоимость регулируемых гидромашин существенно выше, чем нерегулируемых. Объемный способ регулирования может быть рекомендован для использования только в гидроприводах большой мощности (свыше 15 кВт), так как при этом условии можно ожидать, что затраты, сделанные при создании гидропривода, окупятся в процессе его эксплуатации.
7.5. Системы синхронизации движения выходных звеньев нескольких гидродвигателей
В процессе работы гидроприводов различных машин возникает необходимость в одновременном действии нескольких исполнительных гидродвигателей, к которым рабочая жидкость подается от одного насоса. Так как жидкость течет по пути наименьшего сопротивления, то в общем случае выходные звенья гидродвигателей не будут перемещаться синхронно: выходное звено гидродвигателя, для перемещения которого требуется меньший перепад давления, перемещается быстрее, чем выходное звено гидродвигателя, для перемещения которого требуется больший перепад давления. Возможны также случаи, когда при некоторых сочетаниях нагрузок выходное звено одного из двигателей совсем не будет перемещаться. Системы, устраняющие этот недостаток, называются системами синхронизации. В гидроприводах наибольшее распространение получили дроссельные и объемные способы синхронизации движения выходных звеньев нескольких гидродвигателей.
7.5.1. Дроссельные способы синхронизации
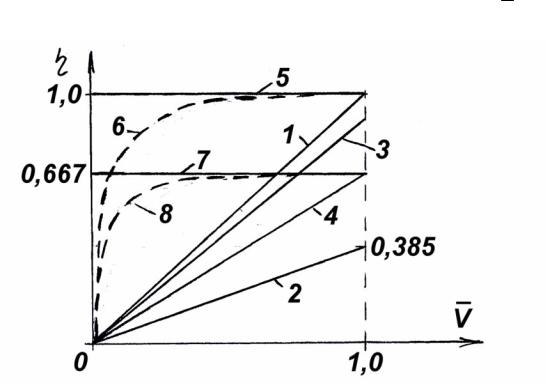
При дроссельном способе синхронизации используют дроссельные делители потока.
На рис. 7.19,а приведена конструктивная схема дроссельного делителя потока, принцип действия которого основан на выравнивании гидрав-
219
лических сопротивлений двух гидролиний за счет автоматического изменения проходного сечения двух регулируемых гидродросселей.
а) |
б) |
Рис. 7.19. Дроссельный делитель потока:
а) конструктивная схема; б) условное обозначение
Рабочая жидкость подводится от насоса к дроссельному делителю потока 1 и через балансные гидродроссели Д1 и Д2, имеющие одинаковые характеристики, попадает в торцевые полости А и Б делителя, между которыми расположен цилиндрический плунжер 2, свободно перемещающийся в корпусе делителя. Смещение плунжера 2 относительно корпуса делителя изменяет проходные сечения регулируемых гидродросселей Д3 и Д4. Далее рабочая жидкость из полостей А и Б делителя через регулируемые гидродроссели Д3 и Д4 поступает в рабочие полости гидроцилиндров, скорости V1 и V2 поршней которых необходимо синхронизировать.
При равных давлениях p1 и p2 в рабочих полостях гидроцилиндров давления в полостях А и Б также одинаковы, плунжер 2 находится в нейтральном положении, при котором регулируемые гидродроссели Д3 и Д4 имеют одинаковое сопротивление.
Деление потока обеспечивается при помощи балансных гидродросселей Д1 и Д2 в соотношении Q1 Q2 = S1 S2 , где S1 и S2 – площади проходных
сечений балансных гидродросселей Д1 и Д2. При S1 = S2 расходы Q1 = Q2. В случае неравенства давлений p1 и p2 в рабочих полостях гидроци-
линдров возникает соответствующий перепад давления в полостях А и Б на торцевых поверхностях плунжера 2. В результате плунжер 2 смещается из среднего положения, изменяя проходные сечения регулируемых гидродросселей Д3 и Д4 (уменьшается проходное сечение регулируемого гидродросселя, через который жидкость поступает в гидроцилиндр с меньшим значением необходимого давления, и увеличивается проходное сечение
220
