Физические случайные величины.

Оставляя в стороне строгое математическое определение случайных величин и ограничиваясь физическими случайными величинами можно сказать, что случайными величинами являются величины, значение которых не может быть точно определено. Причем под определенным значением здесь надо понимать значение, полученное в результате прямых или косвенных измерений. Прямое измерение -- это непосредственное измерение интересующей нас величины, а косвенное -- это определение значения искомой величины по измеренным значениям других величин с помощью функциональной связи (эмпирической или теоретической) между этими величинами.

Физические случайные величины можно условно разделить на 3 разных класса. К первому классу относятся величины, которые имеют в природе строго определенное значение. Это значение мы можем измерить, но из-за неидеальности измерительных приборов измеренное значение будет отличаться от точного. Мы можем много раз повторять наши измерения и каждый раз получать различные значения. При этом случайной величиной будет именно измеренное значение исходно совершенно нормальной величины. К первому классу можно отнести практически все классические физические величины. Ко второму классу можно отнести физические величины статистической физики, истиные значения которых сами по себе являются случайными величинами, флуктуирующими вокруг своих средних значений. К третьему классу относятся квантовые величины. Квантовая величина может не иметь определенного значения (например если квантовая система находится в смешанном состоянии), однако в процессе измерений мы с определенной вероятностью фиксируем некоторое ее значение. Кроме того, согласно принципу неопределенности, одновременно не могут быть точно определены значения величин, описывающихся некоммутирующими операторами. Несовпадение результатов различных измерений для величин из 2 и 3 классов обусловлено не только погрешностью наших измерительных приборов, но и самой природой измеряемых величин.

При интерпретации результатов эксперимента надо учитывать возможное влияние измерений на состояние физической системы, при котором результаты измерений зависят от порядка их проведения. При измерениях классических физических величин таким влиянием часто можно пренебрегать, хотя и не всегда. При измерениях квантовых величин таким влиянием почти всегда пренебрегать нельзя. Исключением может являться случай больших систем, когда каждое отдельное измерение, изменяющее состояние малой части системы, практически не меняет состояние системы в целом.

Какой бы ни была наша наблюдаемая величина, перед нами встает вопрос о повторяемости результатов измерений и их ошибках. Мы можем по-разному организовать наши наблюдения. А именно, мы можем на одной экспериментальной установке измерять одну и туже величину в одной и той же физической системе в разные последовательные моменты времени. Или же мы можем создать несколько одинаковых физических систем вместе с идентичными экспериментальными установками (в статистике такое множество систем обычно называется ансамблем) и измерять интересующую нас физическую величину одновременно во всех системах. Конечно можно и комбинировать эти два метода.

Проводя серию измерений первым способом, повторяющихся результатов можно ожидать только если характерное время изменения измеряемой величины существенно превышает время одиночного измерения и процесс измерения не влияет на состояние системы. В этом случае результат измерений не зависит от очередности их проведения, хотя и содержит случайную составляющую, связанную с ошибками измерений. Второй же метод проведения измерений даст повторяющиеся результаты, если мы сможем создать ансамбль идентичных невзаимодействующих физических систем. Таким образом, если измерения не влияют на систему и состояние системы не зависит от времени, то серии измерений, проведенных первым и вторым способом, эквивалентны и с точностью до ошибок измерения дают повторяющиеся результаты.

Вещественные случайные величины могут принимать как дискретные, так и непрерывные значения как в ограниченных, так и в неограниченных областях вещественной оси. Можно ввести понятие вероятности дискретной случайной величины

,

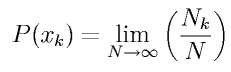определенное если этот предел существует. Здесь N_k - число измерений, в которых величина x=x_k, а N - полное число измерений. Эта вероятность определяет, сколько раз случайная величина x принимала значение x_k относительно полного числа измерений в пределе больших N. Для непрерывных величин аналогично вводится плотность вероятности p(x), так что

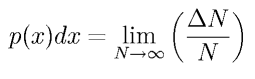
определяет сколько раз величина x принимала значения на отрезке [x,x+dx] относительно полного числа измерений в пределе больших N. Не представляет труда обобщение на случай комплексных и векторных случайных величин.

Для вероятности выполняются очевидные из определений соотношения нормировки:

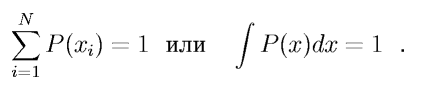
Если существует предел

,

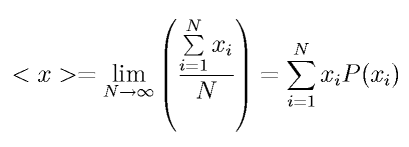то величина <x> называется математическим ожиданием дискретной случайной величины x. Для непрерывной случайной величины определение математического ожидания обобщается как

.

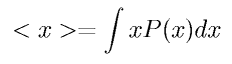Эти пределы имеют смысл не для всех случайных величин, но нас интересуют случайные величины, для которых пределы существуют и определения корректны.

Из определений вероятности (плотности вероятности) и математического ожидания очевидно следуют следующие свойства: 1.  Если x - случайная величина с распределением P_x(x), а y=const - постоянная, то случайная величина z=(x+y) подчиняется распределению P_z(z)=P_x(z-y) и <z>=<x>+y; 2.  Если x - случайная величина с распределением P_x(x), а y=const - постоянная, то случайная величина z=x*y подчиняется распределению P_z(z)=P_x(z/y) и <z>=<x>*y.

Случайная величина A называется независимой от величины B, если вероятность получить при измерениях некоторое значение величины A не зависит от значения величины B. Если A не зависит от B и B не зависит от A, то эти случайные величины называются независимыми. Очевидно, что при этом вероятность получить пару (AB) равна произведению вероятностей получить A и B, то есть P(AB)=P(A)P(B). Это определение легко обобщается на произвольное число случайных величин, а именно случайные величины A₁,A₂,...,A_N называются независимыми, если вероятность получить любое множество вида (A_iA_j...A_k) равна произведению вероятностей получить отдельные значения этих величин: P(A_iA_j...A_k)=P(A_i)P(A_j)...P(A_k).

Коррелятором двух случайных величин x,y называется величина Cor(x,y)=<xy>-<x><y>. Справедливо утверждение, что если случайные величины x,y независимы то Cor(x,y)=0, которое непосредственно следует из определения вероятностей, математического ожидания и равенства 

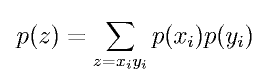
для независимых случайных величин (приведена формула для дискретных случайных величин). Обратное утверждение в общем случае неверно. Но для случайных величин, распределенных по нормальному закону равенство Cor(x,y)=0 является не только необходимым, но и достаточным условием независимости величин x,y. Доказательство может быть найдено практически в любом учебнике по теории вероятностей, например, вИвченко и Медведев 1984.

Существует бесконечно много возможных вероятностных распределений, но некоторые из них встречаются в природе в статистике гораздо чаще других. Некоторые из таких распределений, особенно важные для нас, рассмотрены далее.

Вопрос №12

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физикеионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

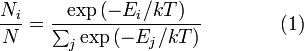где   является числом молекул имеющих энергию   при температуре системы  ,   является общим числом молекул в системе и   — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем  , обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.