[Править]Нормированность волновой функции

Волновая функция   по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющему вид:

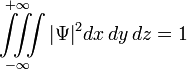
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.

[Править]Матричная и векторная формулировки

Волновая функция одного и того же состояния в различных представлениях — будет соответствовать выражению одного и того же вектора в разных системах координат. Остальные операции с волновыми функциями так же будут иметь аналоги на языке векторов. В волновой механике используется представление, где аргументами пси-функции является полная система непрерывных коммутирующих наблюдаемых, а в матричной используется представление, где аргументами пси-функции является полная система дискретных коммутирующих наблюдаемых. Поэтому функциональная (волновая) и матричная формулировки очевидно математически эквивалентны.

[Править]Философский смысл волновой функции

Волновая функция представляет собой метод описания чистого состояния квантовомеханической системы. Смешанные квантовые состояния (в квантовой статистике) следует описывать оператором типа матрицы плотности. То есть, некая обобщённая функция от двух аргументов должна описать корреляцию нахождения частицы в двух точках.

Следует понимать, что проблема, которую решает квантовая механика, — это проблема самой сути научного метода познания мира. Если представить себе бильярдный стол, закрытый непроницаемой крышкой, и единственным способом исследования вопроса, есть ли на нём бильярдные шары, предположить закатывание в стол других шаров, то мы и получаем ту самую проблему, для решения которой привлечён метод квантовой механики. Пока вброшенный шар проходит сквозь стол без изменения траектории, предсказуемо, мы можем сделать вывод о том, что на траектории шара других шаров нет. Если в результате взаимодействия шаров на столе мы получаем выкатившиеся несколько шаров с различными конечными импульсами и точками, в которых шары покинули стол, то мы можем лишь предполагать о том, каким образом происходило взаимодействие в системе. Если же лузы в бильярдном столе ограничивают возможность шаров покидать стол (энергетический барьер), то система запутывается ещё больше. Подобный пример с бильярдом очень наглядно демонстрирует те трудности, с которыми сталкиваются исследователи, разрабатывая инструменты квантовой механики.

Вопрос 16

Рассмотрим поведение квантово-механической частицы при прохождении через потенциальный барьер конечной ширины (рис.1.7). Ограничимся рассмотрением одномерной задачи, когда ось x параллельна движению частицы. В каждой из трех областей I, II и III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Эта задача моделирует многие физически важные явления, например, выход электронов из металлов, распад атомных ядер и др.

          Уравнение Шредингера в этом случае будет иметь вид

 

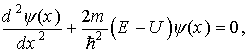                                                                     (1.40)

 

где потенциальная энергия

 

,

 

E - полная энергия частицы.

          В области I уравнение (1.40) будет иметь вид

 

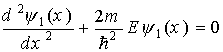                                                                          (1.41)

 

Частное решение уравнения (1.41) будем искать в виде волны, распространяющейся вдоль положительного направления оси x:

 

                                                  .                                                 (1.42)

 

Подставляя (1.42) в (1.41), получим

 

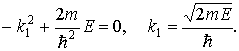                                                                      (1.43)

 

Общее решение уравнения (1.41) для области I представляет собой суперпозицию плоских волн, распространяющихся в противоположных направлениях оси x:

                                           .                                      (1.44)

 

Для области II уравнение Шредингера запишется в виде

 

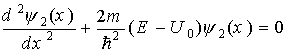                                   .                         (1.45)

 

Общее решение этого уравнения будет иметь вид

 

                                     ,                                        (1.46)

 

где волновое число в области II

 

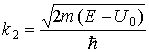                                       .                                                 (1.47)

 

Уравнение Шредингера для микрочастицы в области III будет иметь тот же вид, что и в области I. Общее решение для этой области будет отличаться от решения (1.44) тем, что в области III нет отраженной волны (b₃ = 0)

 

                                                  .                                                  (1.48)

 

          Для вычисления коэффициентов a₁, b₁, a₂, b₂ и a₃ воспользуемся граничными условиями, согласно которым на границах областей волновая функция и ее первая производная должны быть непрерывны.

 

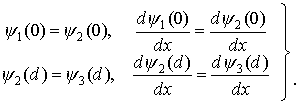                                                         (1.49)

 

Для простоты вычислений можно положить a₁=1, т.к. все коэффициенты b₁, a₂, b₂ и a₃ можно, не изменяя общности задачи, разделить на a₁. Тогда из условий (1.49) получим систему алгебраических уравнений относительно неизвестных b₁, a₂, b₂ и a₃

 

                                                                     (1.50)

 

          В случае, когда энергия частицы меньше высоты потенциального барьера (E < U), волновое число k₂ будет мнимым и его можно представить в виде k₂ = ik, где

 

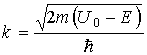 - действительное.

 

Вероятность обнаружить частицу за потенциальным барьером (в области III) равна квадрату модуля амплитуды, прошедшей в эту область волны: D = |a₃|² = = a₃a₃^* . Величину D называют коэффициентом прозрачности барьера.

          Решая систему уравнений (1.50) с учетом граничных условий (1.49), получим следующее выражение для коэффициента прозрачности:

 

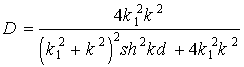                                     .                               (1.51)

 

Формулу (1.51) можно значительно упростить, если положить

 

,

 

что для реальных ситуаций справедливо, и пренебречь слагаемыми, значительно меньшими, чем экспонента. Тогда

 

                                           .                                    (1.52)       

 

Отсюда видно, что проницаемость барьера сильно зависит от  ширины барьера d и величины U₀ - E.

          В случае потенциального барьера произвольной формы (рис. 1.8) проницаемость барьера выражается приближенной формулой

Рис. 1.8. Потенциальный барьер произвольной формы

 

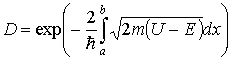,                                                                      (1.53)

 

которая, как нетрудно увидеть, является обобщением формулы (1.52).

          Таким образом, квантово-механической частице для преодоления потенциального барьера необязательно иметь энергию больше, чем высота барьера. Она как бы проходит через “туннель” (заштрихованная область на рис. 1.8), расположенном на высоте E, где E - полная энергия микрочастицы. В связи с этим рассмотренное явление называют туннельным эффектом.

Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.

Гамильтониан квантового осциллятора массы m, собственная частота которого ω, выглядит так:

В координатном представлении   ,  . Задача об отыскании уровней энергии гармонического осциллятора сводится к нахождению таких чисел E при которых следующее дифференциальное уравнение в частных производных

имеет решение в классе квадратично интегрируемых функций.

Для

решение имеет вид:

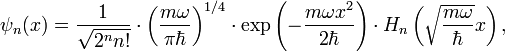
функции   — полиномы Эрмита:

Данный спектр значений E заслуживает внимания по двум причинам: во-первых, уровни энергии дискретны и равноотстоящи, то есть разница в энергии между двумя соседними уровнями постоянна и равна  , во-вторых наименьшее значение энергии равно  . Этот уровень называют основным, вакуумом, или уровнем нулевых колебаний.