45. Марковские процессы. Пример вычисления долгосрочных стационарных вероятностей в методе полного перебора в модели с бесконечным числом этапов.

Пусть в задаче имеется 8 стационарных стратегий. Матрицы переходных вероятностей и доходов для стратегий 1 и 2 выглядят следующим образом:

,

,

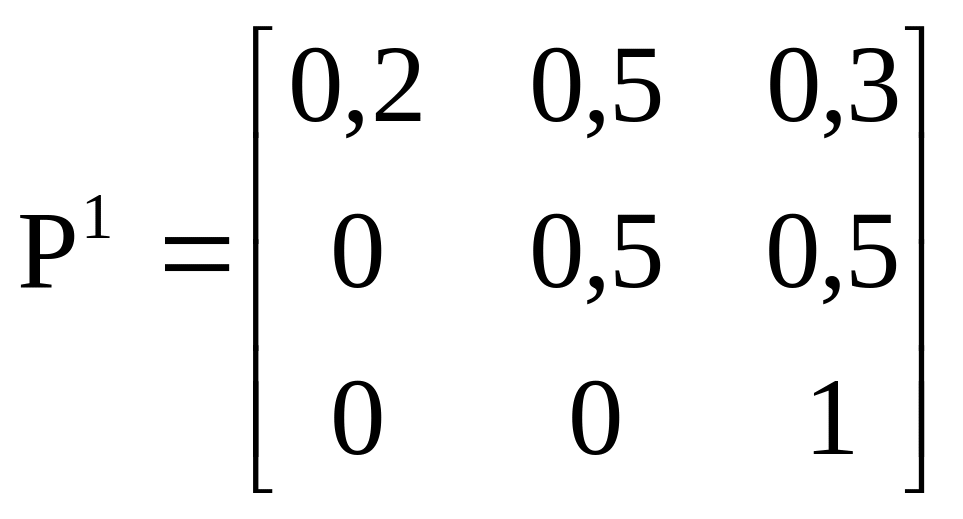Остальные матрицы и для стратегий от 3 до 8 получаются из аналогичных матриц для стратегий 1 и 2.

Долгосрочные стационарные вероятности находятся из уравнений:

Рассмотрим нахождение стационарных вероятностей, используя вторую стратегию. При этом вышеприведенные уравнения примут вид:

Одно из этих уравнений будет избыточным. Решая систему из трех уравнений, получаем следующие значения стационарных вероятностей:

46. Марковские процессы. Характеристика результирующей таблицы в методе полного перебора в методе с бесконечным числом этапов.

Результаты вычислений (долгосрочные стационарные вероятности матрицы переходных вероятностей , соответствующие стратегии ) и (ожидаемый доход за один шаг (этап) при выбранной стратегии ) для всех стационарных приведены в следующей таблице:

s	π1	π2	π3	E
1	0	0	1	-1
2	6/59	31/59	22/59	2,256
3	0	0	1	0,400
4	0	0	1	-1,000
5	5/154	69/154	80/154	1,724
6	0	0	1	-1,000
7	5/137	62/137	70/137	1,734
8	12/135	69/135	54/135	2,216

Как видно из таблицы, стратегия 2 дает наибольший доход. Следовательно, стратегия 2 является оптимальной.

47. Марковские процессы. Недостаток метода полного перебора в модели с бесконечным числом этапов.

Чтобы оценить трудности, связанные с применением метода полного перебора, предположим, что у садовника вместо двух имеется четыре стратегии поведения (альтернативы): не удобрять, удобрять один раз в сезон, удобрять дважды и удобрять трижды в сезон. В этом случае общее число стратегий, имеющихся в распоряжении садовника, составляет 44 = 256 стационарных стратегий. Таким образом, при увеличении числа альтернатив с 2 до 4 число стационарных стратегий возрастает по экспоненте с 8 до 256. Трудно не только перечислить в явном виде все эти стратегии, но и может оказаться также недопустимо большим объем вычислений, требуемых для оценивания всего множества стратегий.

48. Марковские процессы. Модификация рекуррентного уравнения в методе итераций по стратегиям при бесконечном числе этапов.

Метод итераций по стратегиям основывается на следующем. Для любой конкретной стратегии ожидаемый суммарный доход за n-ый этап определяется рекуррентным уравнением.

Это уравнение и служит основой метода итераций по стратегиям. Однако, чтобы сделать возможным изучение асимптотического поведения процесса, вид уравнения нужно немного изменить. В отличие от величины n, которая фигурирует в уравнении и соответствует i-му этапу, обозначим через η число оставшихся для анализа этапов. Тогда рекуррентное уравнение записывается в виде:

Здесь – суммарный ожидаемый доход при условии, что остались не рассмотренными η этапов. При таком определении η можно изучить асимптотическое поведение процесса, полагая при этом, что . Обозначим через вектор установившихся вероятностей состояний с матрицей переходных вероятностей и пусть — ожидаемый доход за этап, тогда можно показать, что при достаточно большом η. , где - постоянный член, описывающий асимптотическое поведение функции при заданном состоянии i.

Так как представляет суммарный оптимальный доход за η этапов при заданном состоянии i, а Е -ожидаемый доход за один этап, то интуитивно понятно, почему величина , равна сумме и поправочного числа , учитывающего определенное состояние i. При этом, конечно, предполагается, что число η достаточно велико. Теперь рекуррентное уравнение можно записать в следующем виде.

Упростив это уравнение, получаем:

,

т.е. имеем m уравнений с неизвестными и E.

Конечной целью является определение оптимальной стратегии, приводящей к максимальному значению Е. Так как имеется m уравнений с неизвестными, оптимальное значение Е нельзя определить за один шаг. В связи с этим используется итеративная процедура, начинающаяся с произвольной стратегии, а затем определяется новая стратегия, дающая лучшее значение Е. Итеративный процесс заканчивается, если две последовательно получаемые стратегии совпадают.