9. Множественная регрессия. Гипотеза «длинная-короткая» модель. Специфика модели. Исключение существенной переменной. Включение несущественной переменной. Пошаговая регрессия.

Множественная регрессия – это прогнозирование единственной переменной y на основании нескольких переменных Х. Она широко используется в решении проблем спроса, доходности акций, при изучении функций издержек производства. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное воздействие их на моделируемый показатель. Построение уравнения множественной регрессии начинается с выбора спецификации модели. Суть проблемы спецификации включает в себя два вопроса: отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессии., должны отвечать требованиям: 1. быть количественно измеримы. Если необходимо включить качественный фактор, то нужно придать ему количественную определенность. 2. не должны быть коррелированны между собой и тем более находиться в точной функциональной связи.

Пусть есть линейная модель: , .

Y зависит от k факторов .

- параметры (коэффициенты) модели, - случайные возмущения.

Матричная форма записи модели: . Два уравнения регрессии:

1. Теоретическая регрессия: , где - случайные возмущения.

2. Модельная регрессия: y_i=b₀+b₁x_i1+...+b_kx_ik+e_i, где e_i - остатки, а . b₁ – оценки коэффициентов β_i.

Спецификация модели - это список параметров, входящих в модель (сам выбор регрессоров).

Исследования модели, как правило, базируются на правильной спецификации модели, т.е. утверждении, что зависимая переменная y, регрессоры X и оцениваемые параметры β связаны соотношением: y=X*β+ε (истинная модель).

Однако на практике в процессе спецификации модели (собственно самого выбора регрессоров) возникают ситуации, когда в оцениваемой модели отсутствует часть независимых переменных, имеющихся в истинной модели (исключение существенных переменных) или присутствуют независимые переменные, которых нет в истинной модели (включение несущественных переменных).

Включение несущественных переменных: модель - Y=X*β+Z*γ+ε, истина - Y=X*β+ε → вводя лишний параметр, мы увеличиваем дисперсию оценок и ошибок, т.о. понижая точность предсказания. Последствия:

-Оценки коэффициентов при прочих переменных остаются несмещенными

-стандартные ошибки растут, t-статистика уменьшается, эффективность оценок ↓.

-Не теряется возможность правильной оценки и интерпретации уравнения

-Несущественная переменная может быть значимой, уравнение с ней – давать лучший прогноз

-Увеличивается риск мультиколлинеарности.

Исключение существенных переменных: модель - Y=X*β+ε; истина (процесс, порождающий данные) - Y=X*β+Z*γ+ε → в данном случае коэффициент β оказывается смещенным и мы проверяем модель на «длинную-короткую» регрессию. Последствия:

• Коэффициенты при оставшихся в модели переменных могут оказаться смещенными

• Их стандартные ошибки t-статистики и другие показатели качества становятся некорректными и не могут быть использованы для суждения о качестве уравнения.

• Уменьшается возможность правильной оценки и интерпретации уравнения.

Тест на выбор «длинной» или «короткой» регрессии. Данный тест используется для отбора наиболее существенных объясняющих переменных. Например, переход от большого числа исходных показателей состояния анализируемой системы к меньшему числу наиболее информативных переменных может быть обусловлен дублированием информации, доставляемой сильно взаимосвязанными признаками или неинформативностью признаков, мало меняющихся при переходе от одного объекта к другому. Так, если две какие-либо объясняющие переменные сильно коррелированы с результирующим показателем Y и друг с другом, то часто бывает достаточно включения в модель одной из них, а дополнительным вкладом от включения другой можно пренебречь.

Пусть . Предположим, что модель не зависит от последних объясняющих переменных и их можно исключить из модели. Это соответствует гипотезе , т.е. последние коэффициентов равны .

Тест по проверке данной гипотезы состоит в следующем:

1. Построить по МНК «длинную» регрессию по всем параметрам 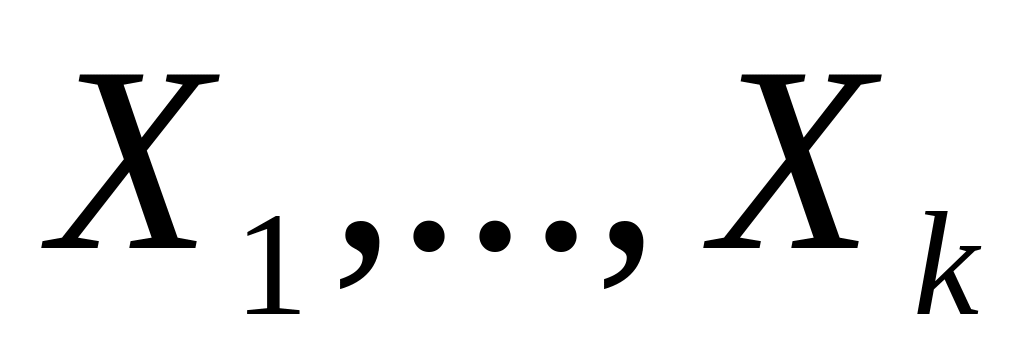и найти для нее .

2. Используя МНК, построить «короткую» регрессию по первым параметрам и найти для нее .

3. Вычислить F-статистику:

4. Найти критическую точку распределения Фишера при выбранном уровне значимости : .

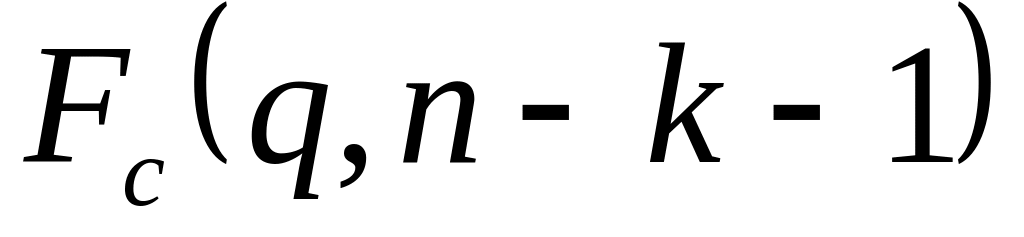5. Если , то гипотеза отвергается, т.е. следует использовать «длинную» модель. Если , то гипотеза принимается, т.е. лучше «короткая» модель.

Пошаговая регрессия. Процедура отбора объясняющих переменных:

1. Вычисляется rкр для n’=n-k+1 степеней свободы

2. Из множества потенциальных факторов исключаем все те, чей коэф-т корреляции с Y меньше критического r(Y, Xj)<rкр.

3. В модель включается переменная Х1 с максимальным коэф-том корреляции Х_i1: r(Y, Х_i1) = max r(Y,Xj), j = 1,…,k.

4. Затем в модель включается фактор, имеющий макс частный коэф-т коррел. с У без включенных в модель к этому шагу. Х_i1: r(Y, Х_i2| Х_i1) = max r(Y,Xj| Х_i1), j = 1,…,k-1.

5.Шаги 4 и 5 проверяются по F-критерию.