3. Регрессионная модель. Причины включения в модель случайного отклонения. Парная линейная регрессия. Мнк. Задачи линейного регрессионного анализа.

Регрессия – способ предсказания значения одних переменных по значениям других.

Регрессионная модель – это уравнение, в котором объясняемая переменная представляется в виде функций от объясняющих переменных факторов.

Задача: на основе эмпирических данных определить объясняемую часть и получить оценку распределения случайной части. Суть: построить регрессию и определить параметры модели.

Парная линейная регрессия - модель статистической линейной связи между двумя количественными переменными х и у, представленная уравнением y = a + bx, где х - переменная независимая , y - переменная зависимая – либо в другой записи Y=B0+B1Xt+Et; Xt-детерминированная величина, Yt-объясняемая переменная, Et – случайная величина.

Детерминированной называется переменная, которая в результате любого числа испытаний принимается одно и тоже конкретное значение из своего множества возможных значений, например, число этажей в конкретном доме

Парная регрессия.

(xi,yi); i=1,…,n

Предполагаем, что yi представляем в виде

Yi=α+βxi+ εi

Смысл εi – однозначно для каждого х мы прогнозировать у не можем

Возникает вопрос о причинах обязательного присутствия в регрессионных моделях случайного фактора (отклонения). Среди таких причин можно выделить наиболее существенные: не включение в модель всех объясняющих переменных, неправильный выбор функциональной формы модели, агрегирование переменных, ошибки измерений, ограниченность статистических данных, непредсказуемость человеческого фактора.

М(у/Х=хi)= α+βxi (мат ожидание у при условии, что Х=хi…)

α и β – истинные значения коэф регрессии

По заданным х и у надо найти α и β

Пусть есть набор значений двух переменных X и Y: ,..., .

Между ними есть объективная связь Y=f(X). Нужно по имеющимся данным наблюдений подобрать функцию , которая наилучшим образом показывает истинную зависимость. , -неизвестные.

Е сли каждую пару представить точкой, то картинка будет – диаграмма рассеяния (корреляционное поле). Требуется найти значения коэффициентов в этой зависимости. Зависимость линейная ŷ= a + bx a^=y – b^x b^=( xy - xy) / (x² – (x)²) – в числителе: среднее произведение минус произведение средних. В знаменателе: средний квадрат фактора минус квадрат среднего.

Наблюдаемые и расчетные значения объясняющей переменной

e – остаток (отклонение, ошибка) – разность между наблюдаемым и расчетным значением. Остаток всегда имеет знак. Остатки наблюдаемы. Надо провести линию регрессии так, чтобы остатки были меньше. Т.о. задача линейной регрессии – провести прямую линию, наилучшим образом приближающую наблюдаемые точки. Провести прямую – найти а и b.

Метод наименьших квадратов

Это метод для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. МНК применяется также для приближённого представления заданной функции другими (более простыми) функциями. В методе наименьших квадратов (МНК) по заданным экспериментальным точкам строится теоретическая функциональная зависимость. Для функции одной переменной по n точкам (xi,yi) ищется "наилучшая" теоретическая кривая y=f(x).

Суть – найти такие коэффициенты a и b, кот. минимизируют сумму квадратов отклонений расчетных значений объясняемой переменной от наблюдаемых значений.

Ŷi=a+bxi

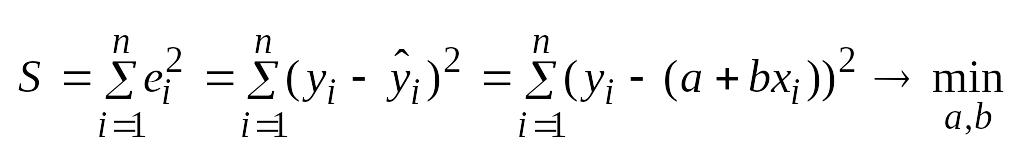в точке .

ei=y-ŷ → ei² = (y-ŷ)²

ŷ = a+bx

Надо построить необходимое условие экстремума (частные производные каждого bj приравниваем к нулю) и решить полученную нормальную систему уравнений линейной регрессии.

Необходимое условие экстремума: если есть функция нескольких переменных S(a,b) то, чтобы найти её экстремум нужно приравнять нулю все её частные производные и решить полученную систему уравнений:

[(yi-(α+βxi)²]’_α= -2(yi-(α+βxi))

[(yi-(α+βxi)²]’_{β =} -2(yi-(α+βxi))xi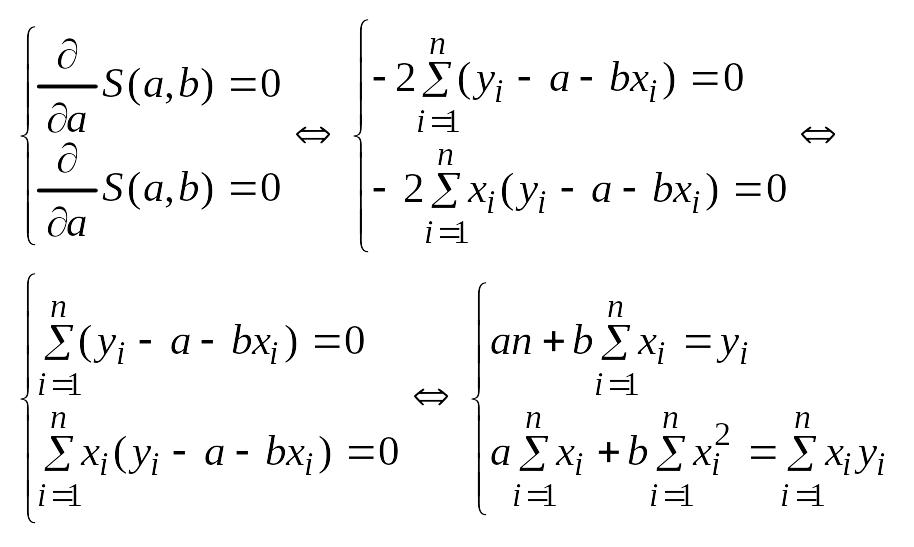

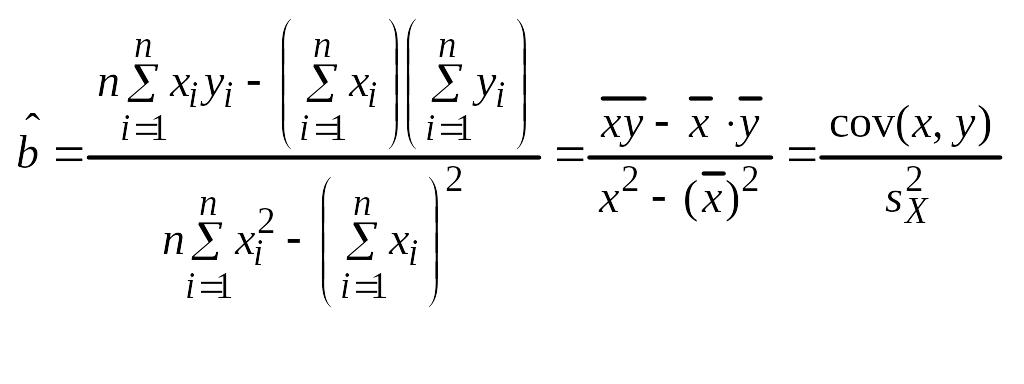
_{Реш-е системы это оценка а и b}

В

X(c чер) = 1/n Σⁿ _i=1 xi

Y(c чер) = 1/n Σⁿ _i=1 yi

числителе – выборочная оценка ковариации; в знаменателе – выборочная оценка дисперсии фактора.

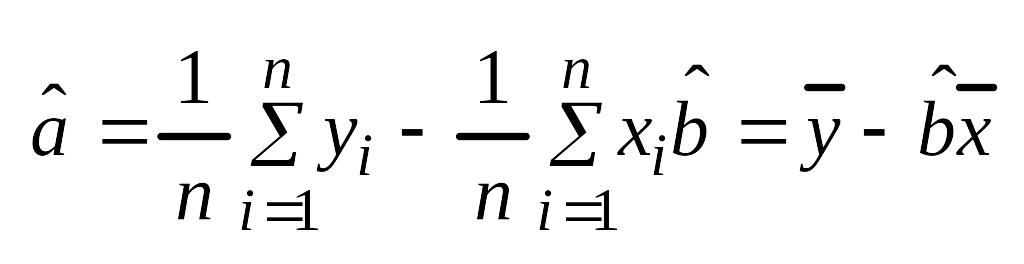
Интерпретация - С ростом Х на 1, Y изменится на значение b.