
- •1. Эконометрика и ее место в ряду других экономических и статистических дисциплин. Типы моделей и типы данных в эконометрике.
- •Общая задача. При помощи статистических методов выразить те закономерности, которые экономическая теория определяет лишь количественно.
- •Эконометрическая модель.
- •2. Коэффициент ковариации. Коэффициент корреляции. Их свойства. Выборочные оценки основных числовых характеристик случайных величин. Проверка значимости коэффициента корреляции.
- •Свойства ковариации
- •3. Регрессионная модель. Причины включения в модель случайного отклонения. Парная линейная регрессия. Мнк. Задачи линейного регрессионного анализа.
- •Парная регрессия.
- •Метод наименьших квадратов
- •4. Основные свойства точечных оценок. Теорема Гаусса-Маркова для однородной модели.
- •6. Проверка гипотез в одномерной модели. Интервальная оценка коэффициентов.
- •7. Множественная регрессия. Мнк. Теорема Гаусса-Маркова для многомерной модели.
- •Метод наименьших квадратов
- •9. Множественная регрессия. Гипотеза «длинная-короткая» модель. Специфика модели. Исключение существенной переменной. Включение несущественной переменной. Пошаговая регрессия.
- •10. Множественная регрессия. Тест Чоу на наличие структурного сдвига. Фиктивные переменные.
- •11. Стохастические (случайные). Обобщенный мнк. Теорема Айткена.
- •13. Гетероскедастичность. Метод взвешенных наименьших квадратов. Коррекция моделей на гетероскедастичность (3 случая).
- •14. Описание тестов проверки на гетероскедастичность (тесты Голдфельда-Куандта, Бреуша-Пагана).
- •15. Мультиколлинеарность: последствия, способы обнаружения, средства устранения. Тест.
- •16. Частный коэффициент корреляции. Его свойства, процедура вычисления.
- •17. Автокорреляция: последствия, способы обнаружения, средства устранения.
- •19. Оценивание моделей с автокорреляцией.
- •Линейные формы: интерпретация регрессии
- •21. Временные ряды. Факторы, влияющие на формирование значений временного ряда. Структура временного ряда. Основные задачи анализа временных рядов.
- •Исследование временноых рядов
- •22. Стационарные временные ряды. Их характеристики. Белый шум. Проверка стационарности временного ряда.
- •Правило проверки гипотезы об отсутствии тренда в тесте серий
- •23.Выравнивание временного ряда (аналитическое – выделение тренда регрессией от времени; механическое – метод последовательных разностей.)
- •3 Основных подхода:
- •24. Автоковариационная и автокорреляционная функция. Способ вычисления. Коррелограмма.
- •25. Линейные модели стационарных временных рядов (авторегрессии и скользящего среднего)
- •26. Модель авторегрессии ar(p). Уравнения Юла Уокера.
- •27. Модель авторегрессии ar (1)
- •28. Модель авторегрессии ar(2). Расчет параметров.
- •29. Модель скользящего среднего ma(1). Расчет параметров.
- •30. Частная автокорреляционная функция. Модели arma(p,q). Свойства acf и pacf.
- •31. Модели arima(p,d,q). Методолгия Бокса-Дженкинса. Интерпретация функций акф и чакф.
2. Коэффициент ковариации. Коэффициент корреляции. Их свойства. Выборочные оценки основных числовых характеристик случайных величин. Проверка значимости коэффициента корреляции.
Ковариацией двух случайных величин называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
Cov (Х,У)= М(ХУ)-М(Х)*М(У)
(Математическое ожидание – сумма произведений значений случайной величины на их вероятности)
Если
X и Y – независимы,
то
![]() Обратное
– неверно!
Обратное
– неверно!
Свойства ковариации
1.
![]() -
ковариация – функция симметричная
-
ковариация – функция симметричная
2.
![]() ,
,
![]()
3.
![]() ,
-
если к одной случ. величине прибавить
const, то ее ковариация с др. случ величиной
не меняется
,
-
если к одной случ. величине прибавить
const, то ее ковариация с др. случ величиной
не меняется
4.
![]() ,
,
![]() -
если одна случ величина умножена на
const, то она выносится вперед
-
если одна случ величина умножена на
const, то она выносится вперед
5. cov(x,y+-z) = cov (x,y) +-cov (x,z) сумма ковариаций 3-х случ величин
6.
![]() -
расчетная формула для дисперсии. Мат
ожидание произведения – произведение
мат ожидания
-
расчетная формула для дисперсии. Мат
ожидание произведения – произведение
мат ожидания
Корреляция - степень, с которой какая-либо одна характеристика воздействует на другую, причем эти характеристики являются взаимосвязанными и образуют пару. Такие парные характеристики могут быть представлены на графике в виде ряда точек. Если все точки на полученной рассеянной диаграмме укладываются на прямую линию (не являющуюся ни горизонтальной, ни вертикальной), то коэффициент корреляции может меняться от +1 (если увеличение одной переменной сопровождается соответствующим увеличением другой) до -1 (если увеличение одной переменной сопровождается постоянным уменьшением другой); коэффициент корреляции, равный 0, свидетельствует о том, что между рассматриваемыми двумя характеристиками не существует никакой зависимости, и они укладываются на одной прямой линии.
Коэффициентом корреляции отражает степень линейной связи между X и Y
Коэффициентом корреляции двух случайных величин называется отношение их ковариаций к произведению средних квадратичных отклонений этих величин:

Свойства коэффициента корреляции
1.
![]()
2.
![]() ,
где a и b=const
,
где a и b=const
3.
![]()
4.
Если X и Y независимы, то
![]()
5.
![]() отражает степень минимальной зависимости
между
отражает степень минимальной зависимости
между
![]() и
и
![]() .
Если
.
Если
![]() ,
тогда
,
тогда
![]() (a, b = const), т.е. X и Y связаны линейно.
(a, b = const), т.е. X и Y связаны линейно.
если
и b=0, то
![]() ,
b>0, то
,
b>0, то
![]() ,
b<0, то
,
b<0, то
![]() .
.
Выборочные оценки основных числовых характеристик случайных величин
Математического
ожидания
![]() для
случ величин в ЭМ анализе (выборочная
средняя)
для
случ величин в ЭМ анализе (выборочная
средняя)
Дисперсии

(квадрат среднего – среднее в квадрате)
Дисперсия – величина, характеризующая степень разброса количественных измерений индивидуальных участков статистической выборки (случайных величин) относительно среднего значения для этой выборки.
Случайная величина – переменная величина, принимающая конкретное значение под воздействием случайных факторов.
Ковариации

Коэффициента корреляции
(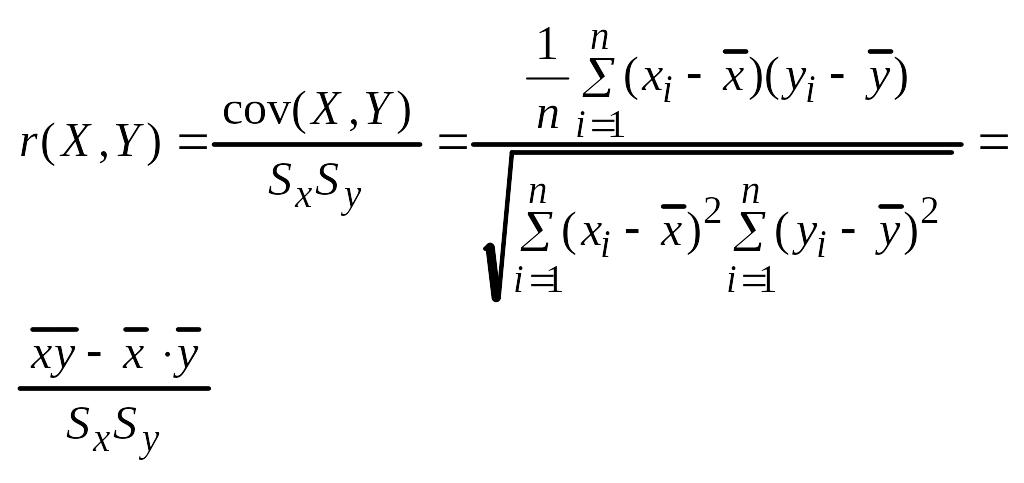 Среднее
произвед - произвед средних/среднее
квадратичное отклонение)
Проверка
значимости коэффициента корреляции
Среднее
произвед - произвед средних/среднее
квадратичное отклонение)
Проверка
значимости коэффициента корреляции
Для проверки значимости коэффициента корреляции формулируются гипотезы: нулевая, что коэффициент равен нулю, т.е. значим H0: r(x,y)=0 и альтернативная H1: r(x,y) не равен 0.
Для вычисленного значения коэффициента корреляции определяют наблюдаемое значение t-статистики:

По
таблице распределения Стьюдента
определяется критическое значение
статистики Т для выбранного уровня
значимости α (например α =0,05) и числа
степеней свободы (n-2)
![]() .
.
Правило проверки гипотизы:
Если
![]() ,
то Н0 отклоняется, т.е. коэффициент
значим.
,
то Н0 отклоняется, т.е. коэффициент
значим.
Если
![]() ,
то H0
принимается, т.е. коэффициент незначим
,
то H0
принимается, т.е. коэффициент незначим
Число степеней свободы (суммы квадратов) - характеристика суммы квадратов (отклонений), показывает, сколько отклонений в сумме квадратов может изменяться "свободно"; обычно обозначается df (degrees of freedom).
