1.8. Октаэдрические напряжения

Определим напряжения в площадках, одинаково наклоненных к главным осям. В этом случае

,

откуда

. (1.27)

Таких площадок четыре. С четырьмя им параллельными они образуют фигуру октаэдра. Поэтому их называют октаэдрическими, и так же называют напряжения, которые действуют в этих площадках (рис. 1.5).

Рисунок 1.5.

Нормальное октаэдрическое напряжение

. (1.28)

Нормальное октаэдрическое напряжение равно среднему нормальному напряжению или одной трети первого инварианта тензора напряжений.

Касательное октаэдрическое напряжение определится из выражения (1.11):

или после раскрытия скобок

, (1.29)

откуда

(1.30)

или, если учесть значения главных касательных напряжений по уравнениям (20),

. (1.30а)

Таким образом, касательное октаэдрическое напряжение равно одной трети корня квадратного из суммы квадратов разностей главных нормальных напряжений или двум третям корня квадратного из суммы квадратов главных касательных напряжений.

Касательное напряжение, выражаемое уравнениями (1.30), принимая интерпретацию М. Роша и А. Эйхингера, называют также интенсивностью касательных напряжений. Другие авторы интенсивность касательных напряжений , согласно Г. Генки, определяют выражением

, (1.30б)

отличающимся от уравнения (1.30) постоянным коэффициентом. Квадрат правой части этого выражения в точности равен второму инварианту девиатора напряжений, взятому с обратным знаком. В отличие от октаэдрического касательного напряжения по равенству (1.30) интенсивность касательных напряжений по уравнению (1.30б) является величиной скалярной.

Величина интенсивности касательных напряжений изменяется в зависимости от вида напряженного состояния (соотношений между компонентами тензора напряжений) в пределах , где – максимальное по абсолютной величине главное касательное напряжение.

От интенсивности касательных напряжений следует отличать интенсивность напряжений или обобщенное напряжение , которое в главных напряжениях выражается

. (1.33)

Величина так же, как и по формуле (30б), представляет собой величину скалярную.

Легко определить, что для линейного напряженного состояния (линейного растяжения или сжатия), когда два из трех главных напряжений равны нулю, интенсивность напряжений по величине совпадает с главным нормальным напряжением, растягивающим или сжимающим.

На основании ранее сказанного о напряженном состоянии точки можно отметить следующие характерные площадки, проходящие через нее:

а) три главные площадки, на которые действуют главные нормальные напряжения, а касательные отсутствуют;

б) шесть площадок, по которым действуют главные касательные напряжения;

в) четыре площадки действия одинаковых по величине октаэдрических напряжений.

Таким образом, всего есть 13 характерных площадок.

1.9. Диаграмма напряжений мора

Диаграмма напряжений по О. Мору (или круги Мора) дает графическое представление о совокупности векторов напряжений нормального и касательного τ, действующих в различных наклонных площадках, рассматриваемых в системе главных осей. Диаграмму эту строят, откладывая величины нормальных напряжений по оси абсцисс, а корреспондирующих им касательных напряжений τ – по оси ординат.

Нормальное напряжение в наклонной площадке определяется выражением (10).

Вместе с тем из уравнений (1.11) и (1.10) следует

. (1.34)

Кроме того, напишем известное условие для направляющих косинусов в виде

. (1.35)

Умножим обе части уравнения (1.10) на (σ₂ + σ₃), затем почленно вычтем результат из уравнения (1.34) и прибавим сюда почленно уравнение (1.35), предварительно умножив обе части его на σ₂σ₃. Таким образом, получим

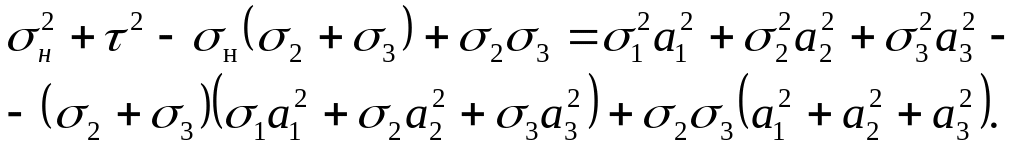(а)

Прибавляя к обеим частям уравнения (а) по , после элементарных преобразований получим

. (1.36а)

Применяя ту же методику, выведем еще два аналогичных уравнения

; (1.36б)

. (1.36в)

Из сравнения полученных уравнений (1.36а, б и в) с известным из аналитической геометрии уравнением окружности

можно заключить, что уравнения системы (1.36) также определяют окружности. Центры их расположены на оси абсцисс (на оси σ_н) и отстоят от начала координат соответственно для уравнений (а), (б) и (в) на расстояния

; и .

В правых частях уравнений (1.36), представляющих собой квадрат радиуса R окружности, есть изменяемый параметр (а₁, а₂ и а₃). Поэтому каждое из уравнений (1.36) является уравнением семейства концентрических окружностей.

Уравнения (1.10), (1.34) и (1.35) определяют корреспондирующие значения напряжений σ_н и τ для заданных условий. При математическом преобразовании этих уравнений в систему (1.36) физический смысл остается неизменным.

Таким образом, первое уравнение системы (1.36) определяет в виде окружности геометрическое место точек σ_н и τ. для того или иного заданного значения направляющего косинуса a₁. То же справедливо и для двух других уравнений системы.

Следовательно, для заданной возможной группы значений направляющих косинусов а₁, а₂ и а₃ величины σ_н и τ определяются (рис. 1.6) точками Р пересечения трех окружностей.

Рисунок 1.6.

Выясним далее, в какой зоне могут быть расположены эти точки. Примем условие σ₁≥σ₂≥σ₃, т.е. индексом 1 обозначим наибольшее (алгебраически) по величине главное нормальное напряжение, индексом 3 – минимальное, а индексом 2 – среднее, промежуточное. Это условие всегда можно соблюсти, поскольку оси координат равно­правны.

Определим величины радиусов R_l, R₂ и R₃ окружностей, заданных уравнениями (а), (б) и (в) системы (1.36) при значениях направляющих коси­нусов соответственно

т.е. для углов α = 90°

; (1.37а)

; (1.37б)

. (1.37в)

Как видно из уравнений (1.36а) и (1.36в), при увеличении значений а₁ и а₃ радиусы соответствующих окружностей увеличиваются. А это значит, что возможные пары значений σ_н и τ находятся на самих окружностях радиусов и или вне их, но не могут располагаться внутри.

Если же увеличивается значение а₂, то радиус R₂ уменьшается, поскольку разность σ₂ – σ₁ отрицательна согласно принятому выше соотношению главных напряжений, и, следовательно, значения σ_н и τ располагаются внутри окружности радиуса R₂ при α₂ = 0.

Проведя окружности радиусами , и , по уравнениям (1.37) из ранее указанных центров получим диаграмму Мора (рис. 1.7). Пары корреспондирующих значений σ_н и τ лежат внутри заштрихованных криволинейных треугольников, ограниченных проведенными окружностями – «главными кругами» Мора. На рис. 1.7 также отмечены характерные точки (А, В, С, D, E, F) диаграммы.

Рисунок 1.7.

Из формул (1.37) видно, что радиусы кругов численно равны величинам главных касательных напряжений.

При помощи построения, показанного на рис. 1.8, по заданным углам α₁, α₂ и α₃ можно определить значения σ_н и τ в наклонной площадке, а также решить обратную задачу. Знак касательного напряжения по диаграмме Мора в общем случае определить нельзя.

Легко заметить, что увеличение или уменьшение напряжений σ₁, σ₂ и σ₃ на одну и ту же величину не изменяет радиусов главных кругов и взаимных расстояний между их центрами. Изменяется лишь положение оси τ. Если ось τ сдвинуть в сторону фигуры (в случае, показанном на рис. 1.7 – вправо) на величину среднего нормального напряжения σ_ср, то получим отображение девиатора напряжений (рис. 1.9). Ось τ в этом случае всегда пересекает фигуру. Ее можно провести при помощи построения, показанного на рис. 1.9, не вычисляя σ_ср.

Рисунок 1.8.

Рисунок 1.9.

Шаровый тензор напряжений отобразится на диаграмме Мора окружностью нулевого радиуса (точкой О’), расположенной на расстоянии σ_ср от начала координат.