1.6. Эллипсоид напряжений
Выразим компоненты напряжений в наклонной площадке формулами (1.8)
,
Откуда
;
;
,
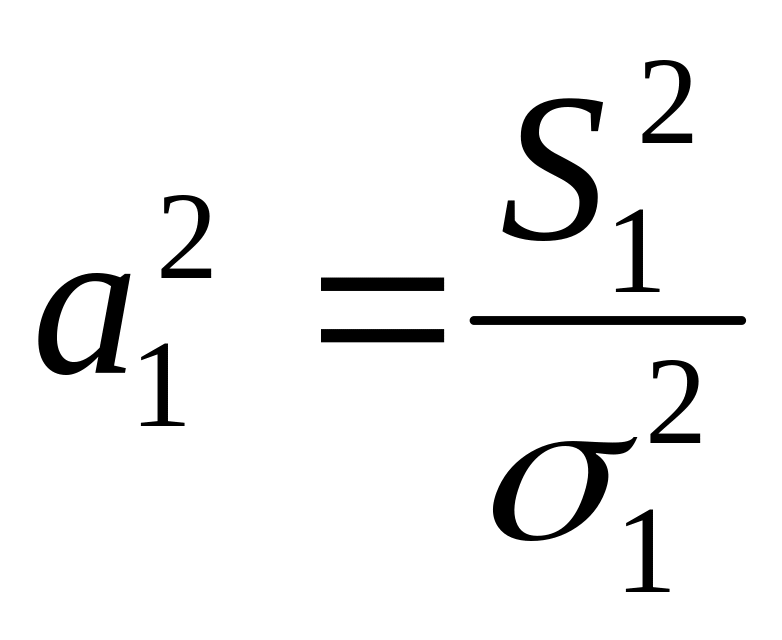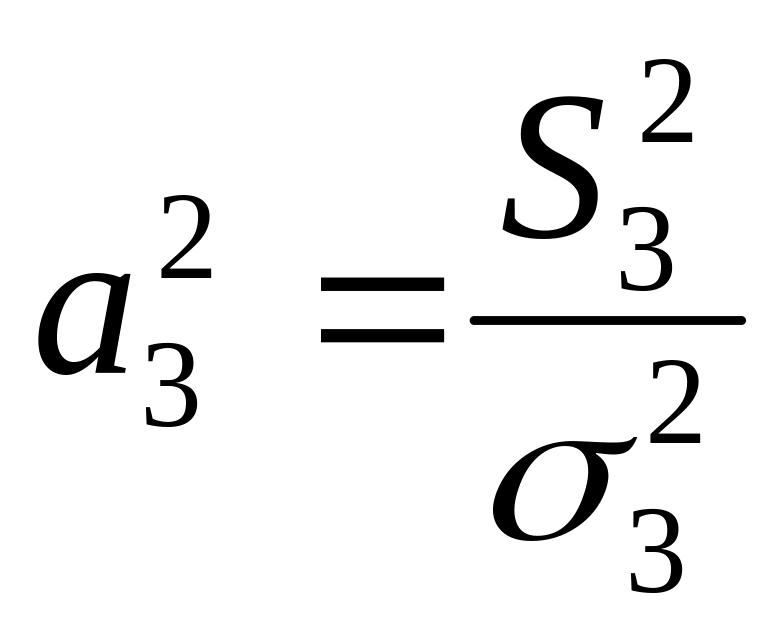но
.
Подставляя в последнее уравнение значения а2 из предыдущих выражений, имеем
(1.18)
σ1, σ2 и σ3для каждого данного напряженного состояния являются постоянными. Уравнение (1.18) является уравнением трехосного эллипсоида, полуоси которого представляют собой главные напряжения в данной точке, а координаты точек поверхности – проекции полного напряжения S для различных наклонных площадок. Следовательно, длина любого отрезка от центра до пересечения с поверхностью эллипсоида (радиуса-вектора) представляет собой полное напряжение S в какой-то наклонной площадке. Эллипсоид этот называется эллипсоидом напряжений (эллипсоидом Ламе) и как бы отражает геометрически тензор напряжений.
Поскольку длина радиусов-векторов эллипсоида ограничена длиной его большой полуоси с одной стороны и малой – с другой, постольку полные напряжения S в различных площадках данной точки по абсолютной величине всегда меньше наибольшего (по абсолютной величине) главного напряжения и больше наименьшего.
Если два из трех главных нормальных напряжений равны между собой по абсолютной величине, то эллипсоид напряжений превращается в эллипсоид вращения.
Если все три главных нормальных напряжения равны между собой и одинаковы по знаку, то эллипсоид обращается в шар и любые три взаимно перпендикулярные оси становятся главными. В этом случае во всех наклонных к осям координат площадках действуют одинаковые равные между собой нормальные напряжения, а касательные отсутствуют, поскольку любая плоскость – главная. Иначе говоря, точка находится в состоянии равномерного всестороннего растяжения или сжатия. Тензор напряжений будет
; (1.19)
этот тензор напряжений носит название шарового тензора. Он инвариантен к выбору системы координат.
Если одно из главных напряжений равно нулю, то эллипсоид превращается в эллипс и объемное напряженное состояние превращается в плоское. Наконец, если два главных напряжения равны нулю, эллипсоид превращается в отрезок прямой линии, что соответствует линейному напряженному состоянию.
1.7. Главные касательные напряжения
Касательные напряжения в наклонных площадках, если тензор напряжений дан в главных компонентах, выражаются уравнением (1.11)
Выясним, в каких площадках касательные напряжения получают экстремальные значения. Из условия
(а)
имеем, например,
.
Подставляя
в выражение (1.11), получим
.
Дифференцируем
по
и приравниваем частотную производную
нулю для нахождения экстремума:
.
Сокращаем
на
и выносим
за скобки:
Меняем
знак, выносим за скобки
и
и делим на 2:
. (б)
Аналогичным
образом дифференцируя уравнение по
и приравнивая частную производную нулю,
получим
. (в)
Решениями
уравнений (б) и (в) прежде всего являются
;
.
Подставляя
в условие (а), найдем
и, таким образом, получаем первую группу
значений направляющих косинусов, при
которых τ имеет экстремум:
; ; .
Далее,
приняв
из уравнения (в), получим
,
а при этих значениях
и
из условия (а) определим соответствующее
значение
и, следовательно, получим вторую
группу значений
,
,
,
определяющую экстремум для τ:
; ; .
Наконец,
подставляя
в уравнение (б), получим
,
а по этим значениям из уравнения (а)
определим
и в результате найдем третью группу
значении
,
,
,
при которых τ имеет экстремум:
; ; .
Далее из условия выражаем и подставляем их значения в формулу (1.11) и производим аналогичные выкладки.
В результате получим следующие шесть групп значений направляющих косинусов, при которых касательные напряжения получают экстремальные значения:
Направляющие косинусы |
Группы значений направляющих косинусов |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
|
|
0 |
0 |
1 |
0 |
|
|
|
0 |
1 |
0 |
|
0 |
|
|
1 |
0 |
0 |
|
|
0 |
Первые
три группы значений направляющих
косинусов определяют координатные
плоскости, которые при рассмотрении
данного вопроса приняты за главные и в
которых касательные напряжения равны
нулю. Следовательно, вторые три группы
значений определяют плоскости, в которых
касательные напряжения достигают
максимальных значений (абсолютных),
поскольку нахождение экстремальных
значений проводилось для
по уравнению (1.11).
Легко видеть, что каждая из этих групп значений выражает плоскости, параллельные одной из координатных плоскостей и составляющие углы 45° с каждой из двух других, или, что то же самое, плоскости, проходящие через одну координатную ось и делящие угол между двумя другими пополам. Таким образом, всего получим (рис. 1.3) три пары (а, б и в) взаимно перпендикулярных площадок, в которых касательные напряжения достигают максимальных абсолютных значений. Из шести этих площадок и шести им параллельных можно составить фигуру ромбического додекаэдра (двенадцатигранника) согласно рис. 1.4.
Рисунок 1.3.
Подставляя в уравнение (1.11) полученные значения направляющих косинусов, найдем значения максимальных касательных напряжений:
(1.20)
Индексы при τ означают, полуразность каких главных напряжений равна данному τ и к каким осям плоскость действия т наклонена под углом 45° (см. рис. 1.3). Эти касательные напряжения называют также главными касательными напряжениями.
Таким образом, главные касательные напряжения равны полу разностям соответствующих главных нормальных напряжений.
Рисунок 1.4.
Наибольшее касательное напряжение равно полуразности алгебраически наибольшего и наименьшего главных нормальных напряжений.
Если все три главные нормальные напряжения равны между собой, то их полуразности и, следовательно, все касательные напряжения обращаются в нуль, т.е. отсутствуют.
Направления главных касательных напряжений на площадках их действия параллельны той главной координатной плоскости, к которой данная площадка является нормальной (рис. 1.3). Вместе с тем направления главных касательных напряжений (на рис. 1.4 показаны стрелками) образуют ребра правильного октаэдра с вершинами ABC на главных осях.
Как видно из уравнения (1.20), сумма трех главных касательных напряжений равна нулю:
. (1.21)
Из этого уравнения следует, что знак наибольшего по абсолютной величине главного касательного напряжения противоположен знаку двух других.
Это условие необходимо соблюдать при назначении знаков главных касательных напряжений в каждой конкретной задаче.
На гранях додекаэдра (рис. 1.4), пересекающихся в точке D, т.е. в точке, расположенной в первом октанте, направления, по которым главные касательные напряжения положительны, указаны стрелками.
Определим значение нормальных напряжений в площадках, по которым действуют главные касательные напряжения, для чего подставляем значения направляющих косинусов в уравнение (1.10):
;
;
, (1.22)
т.е. нормальные напряжения, действующие в площадках главных касательных, равны полусуммам главных нормальных напряжений.
Из выражений (1.20) главных касательных напряжений также видно, что при увеличении или уменьшении главных нормальных напряжений на одну и ту же величину значения главных касательных напряжений не изменятся, т.е. добавление к напряженному состоянию равномерного растяжения или сжатия не изменяет величины касательных напряжений. Это дает возможность всегда представить тензор напряжений в виде суммы двух тензоров.
Обозначим
среднее
нормальное напряжение
через
,
тогда
, (1.23)
т.е. среднее нормальное напряжение равно одной трети первого инварианта тензора напряжений (1.15).
Составим шаровой тензор (1.19):
.
Вычтем этот тензор из тензора напряженного состояния точки, что изображается так:
(1.24)
или
.
Тензор Dσ называется девиатором напряжении. Таким образом, в общем случае тензор напряженного состояния определяется суммой шарового тензора и девиатора напряжений.
Легко видеть, что сумма компонент девиатора напряжений по главной диагонали равна нулю:
.
Напряженное состояние, определяемое шаровым тензором, представляет собой всестороннее равномерное сжатие (о отрицательно) или всестороннее равномерное растяжение. Такое напряженное состояние не может вызвать изменения формы тела – возможно лишь изменение объема (при упругой деформации) и разрушение. Если же напряженное состояние, в котором находится какое-либо тело, определяется девиатором, то тело изменяет форму без изменения объема даже при упругом деформировании.