3.5. Связь между напряжениями и деформациями при пластическом деформировании

Связь между напряжениями и деформациями при пластическом деформировании может быть выведена на основании следующих экспериментально установленных положений.

В каждый данный момент активной пластической деформации, по крайней мере в условиях простого нагружения:

1. направления главных линейных деформаций (удлинений) совпадают с направлениями главных нормальных напряжений;

2. диаграмма Мора для деформаций (в координатах ε и γ) геометрически подобна диаграмме Мора для напряжений (в координатах σ и τ).

Для получения необходимых выводов следует учесть условие постоянства объема

.

Деформация, согласно А. А. Ильюшину, будет в данный мо­мент активной в том случае, если интенсивность напряжений имеет значение, превышающее все предшествующие ее значения. Если меньше хотя бы одного из предшествующих ее значений, то деформация элемента будет пассивной.

Процесс нагружения тела является простым, когда внешние силы от начала их приложения возрастают пропорционально общему параметру».

Построим для какой-либо точки, находящейся в пластическом состоянии, диаграммы Мора для напряжений и деформаций (рис. 3.3).

Рисунок 3.3.

На основании положения о подобии диаграмм Мора для напряжений и деформаций непосредственно из чертежа (рис. 3.3) получим (учитывая знаки деформаций)

; (3.20)

взят как коэффициент пропорциональности. Смысл его будет выяснен в дальнейшем.

Возьмем из уравнения (3.20) выражение

и, заменив в нем на основании условия постоянства объема на , определим :

.

Возьмем теперь из уравнения (3.20) выражение

и, подставив в него найденное значение , получим

.

Решив это уравнение относительно и поступив аналогично с другими сочетаниями уравнений (3.20), получим

(3.21)

Обозначив через окончательно получим

(3.21а)

Так как при пластической деформации объем тела не изменяется( ), то коэффициент 1/2 в уравнении (3.21а) при суммах напряжений представляет собой коэффициент Пуассона. Отсюда следует, что выражения пластических деформаций совершенно аналогичны выражениям для упругих деформаций, с той лишь разницей, что модуль упругости первого рода заменен коэффициентом . Этот коэффициент называют модулем деформации (или модулем пластичности) первого рода.

Модуль упругости второго рода связан с модулем Юнга соотношением

.

Приняв коэффициент Пуассона , имеем

.

Из сравнения уравнений (3.21) и (3.21а) вытекает, что в случае пластической деформации

. (3.22)

Таким образом, является модулем деформации второго рода.

Существенная разница между модулями упругости и , с одной стороны, и модулями деформации и – с другой, состоит в том, что первые величины постоянные – константы материала, а вторые являются величинами переменными, могущими принимать различные значения, из которых каждое действительно только для одного какого-либо момента процесса деформации.

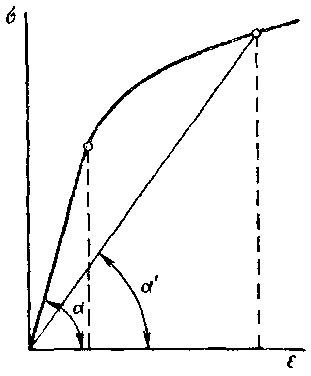
Рисунок 3.4

Из рис. 3.4 видно, что , a , причем является переменным. Отсюда можно охарактеризовать значение следующим образом. Если бы с самого начала деформации модуль имел данную величину , то при получении элементом тела данной деформации величина напряжения была бы .

Пусть . Подставив это значение в первое и второе уравнения (3.21а), получим

; .

Таким образом, если два напряжения равны между собой, то равны и соответствующие деформации.

Если деформированное состояние плоское, то одна из деформаций равна нулю. Подставим в среднее уравнение (3.21), тогда

или

.

Таким образом доказано ранее принятое положение, что при плоском деформированном состоянии напряжение в направлении отсутствующей деформации равно полусумме двух других.

Подставим в то же уравнение (3.21) , т.е. будем иметь в виду плоское напряженное состояние

.

Таким образом, при плоском напряженном состоянии деформация в направлении отсутствующего напряжения пропорциональна полусумме двух других, т.е. среднему напряжению.

Наконец, из уравнений (3.21) видно, что деформация имеет положительный знак, если соответствующее ей напряжение больше полусуммы двух других (алгебраически).

Вернемся к диаграммам Мора для напряжений и деформаций (рис. 3.3). Из их подобия следует

,

а выражая отрезки через напряжения и деформации с учетом знаков (направлений) отрезков, получим

(3.23)

или

. (3.23а)

Поскольку на рис. 3.3 принято , то левая часть равенства (3.23) представляет собой не что иное, как величину [см. уравнение (3.16)]. Правая часть построена аналогично левой. Если левая часть характеризует напряженное состояние, то правую часть можно считать характеристикой деформированного состояния. Обозначив последнюю , можем написать

. (3.24)

что дает еще одну форму выражения связи между напряженным и деформированным состоянием.

Пользуясь интенсивностями напряжений и деформаций , можно написать обобщенное уравнение связи напряжений с деформациями

. (3.25)

Интенсивность деформаций при пластическом формоизменении определяет степень упрочнения материала. Можно утверждать, что интенсивность напряжений при пластической деформации является функцией интенсивности деформаций

. (3.25а)

Кривую , можно построить на основании опытных данных.

Если считать материал несжимаемым и пренебрегать изменением его плотности при деформации, то зависимость между интенсивностями напряжений и деформаций в точности совпадает с диаграммой истинных напряжений при растяжении, поскольку при простом растяжении равно растягивающему напряжению, – относительному удлинению.

Заменяя в правых частях уравнений (3.21а) суммы двух напряжений через разности утроенного среднего напряжения и третьего напряжения (например, ) и выражая из уравнения (3.25) модуль пластичности

, (3.26)

можно получить уравнения связи напряжений и деформаций в следующей форме:

(3.27)

Уравнения (3.21) и (3.27) действительны и в том случае, если главные напряжения и деформации заменить напряжениями и деформациями, данными в произвольных осях х, у, z. Однако при этом необходимо добавить еще три уравнения, связывающие касательные напряжения и сдвиги , а именно:

; ; . (3.28)

Приведенные уравнения связи напряжений и деформаций лежат в основе теории так называемых малых пластических деформаций. Особенностью этих уравнений является то, что коэффициент пропорциональности определяется упрочнением металла и, следовательно, представляет собой функцию деформации. В другой теории, а именно так называемой теории пластического течения, за основу положена связь напряжений со скоростями деформаций (приращениями деформаций). Предпосылки для установления этой связи аналогичны указанным ранее при рассмотрении связи напряжений и деформаций:

1. направления скоростей главных линейных деформаций совпадают с направлениями главных нормальных напряжений;

2. диаграмма Мора для скоростей деформаций геометрически подобна диаграмме Мора для напряжений;

3. объем тела принимается постоянным, что определяется выражением

.

Коэффициенты пропорциональности в уравнениях связи будут другие: вместо обозначений и примем обозначения и .

При этом

. (3.29)

Таким образом, в теории течения принято, что интенсивность напряжений (напряжение текучести) для каждого материала является функцией интенсивности скоростей деформации

. (3.30)

Все уравнения связи напряжений и скоростей деформаций можно написать по аналогии с уравнениями напряжения – деформации. Следует лишь заменить в последних обозначения деформаций обозначениями скоростей деформаций, а равно заменить коэффициенты пропорциональности: например, вместо уравнения (3.20) будет действительно уравнение

.

Теория течения при использовании динамических уравнений равновесия дает возможность решать задачи динамики при пластическом деформировании, а также учитывать сопротивление, зависящее от скорости деформации [уравнение (3.30)]. Эта теория позволяет описать процесс установившейся ползучести.

В случае медленной и непродолжительной деформации деформационная теория и теория течения являются тождественными. При линейной связи интенсивности деформаций со временем интенсивность скоростей деформации не зависит от времени и, следовательно, интенсивность напряжений согласно уравнению (3.30) также постоянна по времени.