Основные понятия и правила теории нечетных множеств

1. Нечеткое множество «С» называется нормальным, если выполняется условие:

Sup _С(х_i) = 1 или = 1, Vx_i  Х. нечеткие множества отличающиеся от нормальных (т.е. Sup _С(х_i) ≠ 1) приводятся к нормальному виду путем деления каждого значения _С(х_i) на max _С(х_i). В основном нечеткая логика оперирует нормальными нечеткими множествами. например, max _С = 0,8 _Сi = 0,3. тогда нормальное значение будет равно .

Замечание.

1) функция принадлежности _С(х_i) не является вероятностью выполнения поставленной цели, поэтому выполнение условия: =1 совершенно не обязательно (у вероятностей выполняется правило: = 1). 0≤ Р_i ≤ 1; Р_q = 0,95;

2) функции принадлежности могут формироваться как для дискретной случайной величин х_i , так и для непрерывной х_i;

3) нечеткой переменной называется совокупность параметров ( ; Х; С ), где - наименование нечетной переменной; Х={х_i} – область определения нечеткой переменной ; С ={ (х_С); х_i} – нечеткое множество на множестве «Х», описывающие ограничения на возможные значения нечеткой переменной (ее семантику).  - для всех; V – или;  - и;  - пересечение множеств;  - объединение множеств;  - если, то.

Лингвистической переменной называется совокупность (, Т, Х, G, М), где:  - наименование лингвистической переменной; Т – множество ее значений (терм – множество); G – синтаксическая процедура (грамматика), позволяющая оперировать элементами терм – множества Т в частности генерировать новые осмысленные термы. Множество Т* = ТUG (Т) называется расширенным терм - множеством лингвистической переменной; М – семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную.

Рассмотрим пример формирования лингвистической переменной.

Пусть эксперты оценивают издержки на доставку грузов с помощью понятий: «малые издержки», «средние издержки», «большие издержки», при этом минимальное значение издержек на конкретном направлении для конкретных грузов и альтернативных видов транспорта будут равны: Э_min=10тыс.у.е., а максимальные издержки: Э_max=80 тыс. у.е. Формируем лингвистическую переменную вида (, Т, Х, G, М), где:  - издержки на доставку; Т=(₁; ₂; ₃), ₁ – малые издержки; ₂ – средние издержки; ₃-большие издержки. «Х» - множество имеющие интервал значений Х_i : Х=[10; 80] . С₁; С₂; С₃ – нечетные множества, характеризующие понятия «малые издержки», «средние издержки», «большие издержки». G - область определения некоторых новых нечетких переменных, например: издержки, близкие к 20 тыс. у.е. или приблизительно равные 75 тыс. у.е.; G = G (х_i). Такие лингвистические переменные называются синтаксически независимыми.

Например:  = (75; х; С_) – приблизительно равна 75 тыс. у.е.

Определение функции принадлежности нечеткой случайной величины

Функция принадлежности _С (х_i) элемента х_i к нечеткому множеству С (интерпретируется) определяется как субъективная мера того, насколько элемент х_i  Х соответствует понятию, смысл которого отражается нечетким множеством «С». Под субъективной мерой понимается определяемая элементами степени соответствия элемента х_i понятию, формализуемому нечетким множеством «С» (возможность интерпретации х_i понятием, заложенным в нечетком множестве «С»).

Рассмотрим некоторые методы построения функции принадлежности на основе экспертных оценок.

Имеется m”экспертов. Часть из них на вопрос о принадлежности элемента х_i  Х нечеткому множеству «С» отвечают положительно (n₁ экспертов), другие на этот вопрос отвечают отрицательно: n₂ = m – n₁. тогда функция принадлежности определяется как вероятность дискретной величины: _С (х_i) = .

Возьмем: m = 6 – максимальная оценка. Х = {1; 2; 3; 4; 5} – множество. Требуется сформировать нечеткое множество «С», определяющее нечеткое понятие «немного больше двух». Результаты опроса экспертов приведены в таблице:

хi	1	2	3	4	5 да нет
n1	0	0	6	4	1
n2	6	6	0	2	5
m	6	6	6	6	6

Получим следующие значения функции принадлежности х_i  Х нечеткому множеству «С» _С (х_i=1) = 0; _С (х_i=2) = 0; _С (3) = 1; _С (4) 0,7 _С (5)  0,2.

Данный метод дает достаточно точно грубое определение функции принадлежности, являясь самым простым.

Второй метод базируется на основе количественного сравнения степеней принадлежности и допускает использование одного эксперта. результатом опроса эксперимента является построение матрицы M= / m_ij /, где i, j = ; n – число точек, в которых сравниваются значения функции. Число m_ij (элемент матрицы) показывает во сколько раз, по мнению эксперта, _С (х_i) больше _С (х_j). При этом количество вопросов к эксперту составляет не n², а (n² - n) / 2, так как: m_ii = 1; m_ji = 1 /m_ij/ Понятия, которые использует эксперт и их представление значениями m_ij следующие:

Понятие Представление в m_ij

1. _С (х_i) примерно равна _С (х_j) 1

2. _С (х_i) немного больше _С (х_j) 3

4 – больше, чем

3. _С (х_i) больше _С (х_j) 5

6 – существенно заметно

больше

4. _С (х_i) заметно больше _С (х_j) 7

8 – много больше

5. _С (х_i) намного больше _С (х_j) 9

6. Значения функции принадлежности _С (х₁); _С (х₂); … _С (х_n) в точках х₁; х₂; … х_n определяются на основе решения задачи:

М^Т Ф^Т = _max  A ,

где: Ф - вектор длиной (Ф₁; Ф₂; …Ф_n);

_max – максимальный элемент матрицы М^Т;

Т - символ транспонирования.

Матрица М^Т называется транспортной по отношению к матрице М, если столбцы матрицы М^Т являются строками матрицы М (нужно повернуть матрицу М вокруг главной диагонали на 180⁰). В результате получает:

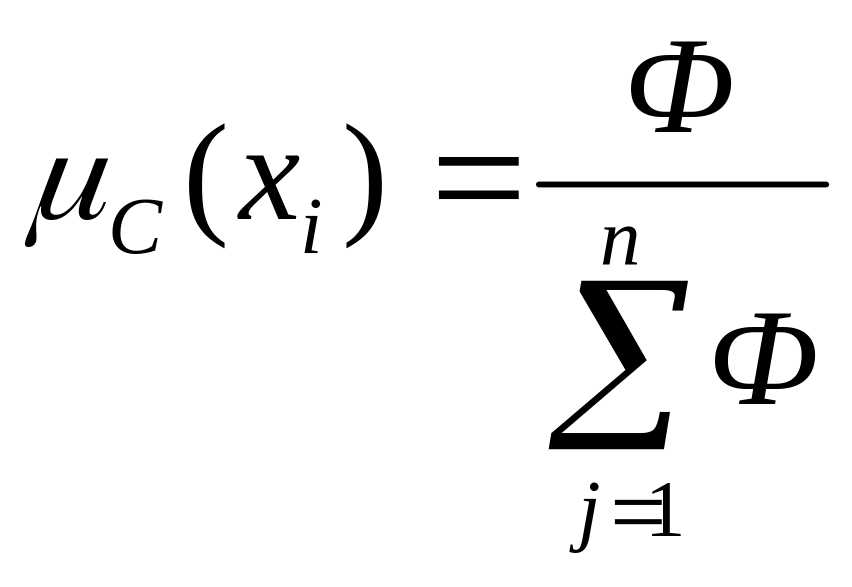или ; *

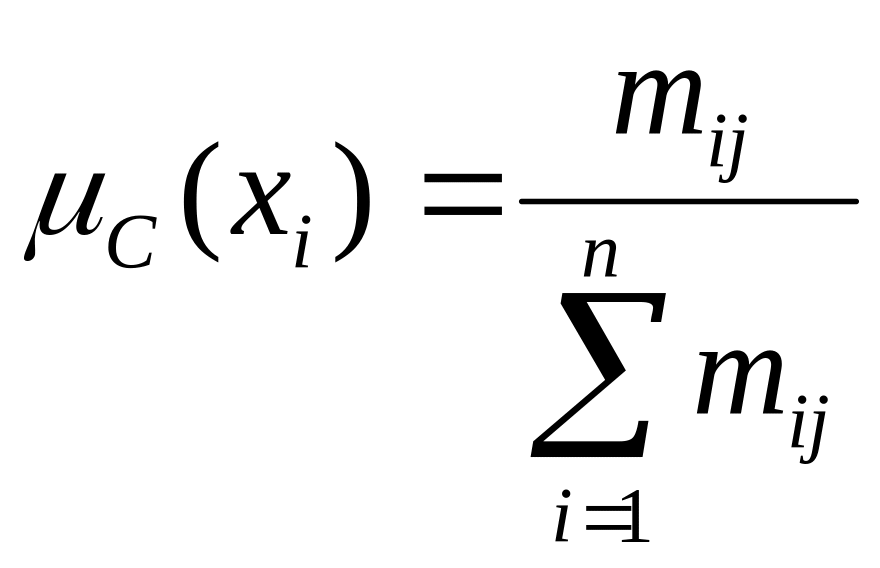i  j = {1, 2, … n}; значение j выбирается произвольно.

Таким образом, для определения величин _С (х_i) необходимо (зафиксировать) получить произвольно выбранный столбец j матрицы М и вычислить отношения значений элементов m_ij к сумме значений элементов столбца j. Выбор значений столбца j практически не влияет на правильность определения функции принадлежности _С (х_i) – при высокой квалификации эксперта.

Пример дать на практике. Для представления расстояния перевозок между двумя пунктами отсутствующими в тарифном руководстве 4-Р, применяется лингвистическая переменная «» - расстояние перевозок с множеством базовых значений Т={малое; среднее; большое}. Базовое множество Х={1; 3; 6; 8}. Терм «малое» характеризуется нечеткой переменной {малое, Х, Č}.

Требуется построить функцию принадлежности _с нечеткого множества Č характеризующего терм «малое», т.е. определить _С (х_i); х_i  Х.

Опросом экспертов получена следующая матрица парных сравнений.

е(х_i) 1 3 6 8

1 1 5 6 7

3 1/5 1 4 6

6 1/6 1/4 1 4

8 1/7 1/6 1/4 1

Например, на пересечении первой строки и второго столбца стоит цифра 5, т.е. m₁₂ = 5, то означает _С (1) больше _С (3) на пересечении

х=1 х=3

второй строки и первого столбца стоит m₂₁ = 1/5, т.е. транспонированное значение, так как мы установили, что m_ji = 1/ m_ij. Фиксируем первый столбец матрицы «М». М₁ = {1; 1/5; 1/6; 1/7}, тогда по формуле * получаем:

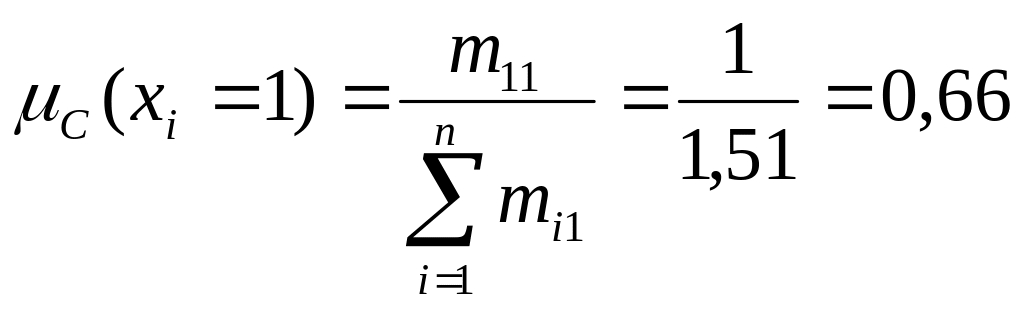
Таким образом, можем записать вид нечеткого множества

Č={0,66/1; 0,13/3; 0,11/6; 0,09/8}.

Нечеткое терм – множество Č является одновременно и нечетким высказыванием «расстояние малое». При его характеристике можно использовать логистические параметры типа: и; или; если; то, которые базируются на нечетких переменных х_i  Х и х_i  Č.

I. Характеристики основных групп операций, используемых в логистике грузодвижения. В логистике грузодвижения используются три основные группы функций.

К чисто логическим функциям относятся:

1. Логистические – 1) хранение, 2) упаковка, 3) маркировка, 4) сбытовые, 5) снабженческие, 6) ростаривание, 7) затаривание.

К транспортным функциям относятся:

2. Транспортные – 1) перегрузочные, 2) перевозка, 3) перевалка, 4) хранение в пунктах перевалки.

К экспедиторским функциям относятся:

3. Экспедиционные – 1) выбор рационального вида транспорта для перевозки;

2) доставка груза от склада отправителя до места погрузки на магистральный вид транспорта и обратно (on-karriеr и pre-karrier);

3) доставка груза в пунктах перевалки с одного вида транспорта на другой;

4) формирование крупных партий груза из мелких отправок с целью полного использования грузоподъемности или грузовместимости транспортного средства и формирования маршрутных отправок и т. д. - Приложение !!

Схема взаимодействия групп операций в системе грузодвижения приведена на рис.++

Пункт отправления

Экспедиционные операции

Логистические операции

Транспортные операции

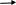
Пункт назначения

Экспедиционные операции

Логистические операции

Линейная перевозка одним видом транспорта

Рис.++ Схема взаимодействия групп операций в системе грузодвижения

Кроме перечисленных к экспедиционным операциям иногда можно отнести часть транспортных операций (перевозка, перегрузка) и операций логистики, если они выполняются транспортно-экспедиционной компанией.

Управление логистикой грузодвижения состоит из следующих основных этапов:

- системный анализ параметров и характеристик системы транспортно-экспедиционного обслуживания потребителей логистических услуг;

- прогнозирование основных параметров работы логистической системы доставки;

- формирование нормативных и плановых показателей системы;

- организация реализации намеченных целей в логистической системе грузодвижения;

- контроль выполнения параметров в процессе работы системы;

- разработка регулирующих воздействий для поддержания системы в установленном состоянии.

Выполнение целей, функций и задач управления логистической системой грузодвижения (логистической транспортной системой) осуществляется с использованием следующих видов обеспечения:

- финансово-экономическое;

- информационное;

- материальное (снабжение ресурсами); - кадровое;

- техническое;

- технологическое;

- методическое;

- организационное.

Финансово-экономическое обеспечение подразумевает получение необходимых инвестиций для формирования и внедрения системы управления логистической грузодвижения.

Информационное обеспечение является одним из основных ресурсных объектов, на использовании которого базируется работа системы управления логистикой. Она содержит: базы данных; методы технологии и правила обработки логистической информации; необходимые программные средства, отвечающие современным требованиям информатизации экономики и общества.

Материальное обеспечение включает ресурсы, необходимые для успешной работы системы управления: компьютерная техника; оборудование и приборы (средства связи), основные средства (здания и сооружения, машины), энергоресурсы и т.д.

Кадровое обеспечение подразумевает укомплектование системы хорошо подготовленными, квалифицированными кадрами. Сюда же входит система их подготовки и переподготовки.

Техническое обеспечение – наличие технических средств, необходимых для успешного решения задач управления (компьютеры, средства телекоммуникаций и вспомогательное оборудование – ксероксы, факсы, принтеры и т.д.

Технологическое обеспечение – предлагает наличие и использование новейших технологий управления (эл. почта).

Методическое обеспечение должно содержать методы решения задач управления (оптимизация, прогнозирование, анализ, регулирование).

Организационное обеспечение, в составе которого разрабатываются: цепи, функции и задачи управления, а также состав и структура элементов его составляющих.