3.3 Приведение квадратичной формы к каноническому виду ортогональным преобразованием

Наиболее простым является такой вид квадратичной формы, который не содержит произведения координат , т.е. представляет собой сумму квадратов.

Вид квадратичной формы

называется каноническим видом квадратичной формы.

Матрица В в этом случае является диагональной матрицей:

.

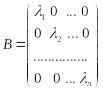Возникает вопрос, какое преобразование приводит квадратичную форму к каноническому виду?

Пусть , где А – симметричная матрица. Известно, что А имеет собственный ортонормированный базис. Обозначим его . Тогда

1. , .

2. , если .

3. , .

Пусть теперь G – матрица перехода от стандартного ортонормированного базиса к базису , т.е. G – ортогональная матрица.

Теорема. При линейной замене переменных квадратичная форма принимает вид

,

где – собственные числа матрицы А.

Действительно. Преобразование запишем в векторной форме

.

Тогда

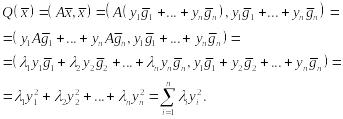
Мы воспользовались тем, что скалярное произведение

.

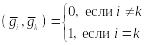Подведем итог сказанному.

Алгоритм приведения квадратичной формы к каноническому виду ортогональным преобразованием.

1. Выписываем матрицу А квадратичной формы.

2. Находим собственные числа матрицы А: .

3. Составляем ортонормированный базис из собственных векторов симметричной матрицы А.

4. Составляем ортогональную матрицу перехода G, столбцами которого служат собственные векторы .

5. Замена позволяет записать квадратичную форму в новых координатах в виде суммы квадратов, т.е. в каноническом виде .

6. Обратное преобразование , и так как G – ортогональная матрица и , то .

Примеры смотри в тренинге умений.

Замечание. Мы рассмотрели здесь лишь один способ приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования. Существуют и другие способы приведения квадратичной формы к сумме квадратов. В зависимости от этих способов квадратичная форма может иметь различные канонические виды. Но несмотря на многообразие канонических видов для данной квадратичной формы неизменными остаются важные характеристики их коэффициентов.

К ним относится, во-первых, ранг квадратичной формы, который равен числу отличных от нуля коэффициентов в любом ее каноническом виде. Ранг равен числу ненулевых собственных значений матрицы квадратичной формы (с учетом их кратности).

Выполняется также закон инерции: сохраняется число положительных, отрицательных и нулевых коэффициентов в каноническом виде квадратичной формы, не зависимо от способа приведения ее к сумме квадратов.

3.4 Приведение кривой второго порядка к каноническому виду

В курсе аналитической геометрии мы изучали эллипс, гиперболу и параболу, которые являются кривыми второго порядка. Напомним их уравнения:

– эллипс,

– гипербола,

, или , – парабола.

При выводе уравнений этих кривых была так подобрана система координат, что уравнения получились “простого”, канонического вида.

Если система координат выбрана произвольно, то уравнение кривой второго порядка имеет общий вид:

, (*)

где . Левая часть этого уравнения состоит из двух частей. Первая часть – квадратичная форма от переменных х, у, с симметричной матрицей

.

Определитель этой матрицы равен .

Оказывается, знак этого определителя, а так же знаки коэффициентов при квадратах А и С играют решающую роль при выяснении вопроса о типе кривой, заданной общим уравнением.

Вторая часть имеет вид

и представляет собой линейную функцию.

Часть линейной функции, не содержащая константу, – линейная форма.

Таким образом, левая часть уравнения (*) есть сумма:

квадратичная форма + линейная форма + константа.

Левая часть уравнения (*) есть многочлен второй степени от х и у. Какие же кривые на плоскости может определить алгебраическое уравнение (*) с условием, что хотя бы один из коэффициентов А, В или С отличны от нуля?

Оказывается, что уравнение определяет уже известные нам эллипс, гиперболу или параболу; кроме того возможны случаи (вырожденные):

1. пара пересекающихся прямых ,

2. пара параллельных прямых ,

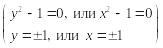3. пара совпадающих прямых ,

4. точка или пустое множество .

В аналитической геометрии доказывается теорема, что других возможностей, кроме перечисленных, быть не может.

Среди невырожденных кривых эллипс и гипербола называются центральными, они имеют единственный центр симметрии, парабола центра не имеет. Канонический вид кривой не содержит произведения координат, а для центральных кривых не содержит и линейной формы.

Важной задачей является задача приведения кривой второго порядка к каноническому виду. Изменением системы координат, а именно поворотом координатных осей и параллельным сдвигом, общее уравнение кривой второго порядка (*) можно привести к каноническому виду.

Только после этого можно говорить о типе кривой.

Определитель матрицы квадратичной формы

не меняется при сдвиге и повороте координатной системы, говорят, что он является инвариантом этих преобразований. В связи с этим линии второго порядка классифицируют по следующим типам:

1) эллиптический, при ;

2) гиперболический, при ;

3) параболический, при .

Такую же классификацию применяют к уравнению (*). Доказывается, что эллипс имеет уравнение эллиптического типа, гипербола – гиперболического, парабола – параболического. Условия эти лишь необходимые, но не достаточные (уравнения эллиптического типа может определить, например, вырожденный в точку эллипс , или пустое множество ).

Не вдаваясь в дальнейшие подробности, опишем алгоритм приведения общего уравнения кривой 2-го порядка к каноническому виду. Используем при этом наше умение привести к каноническому виду квадратичную форму. Итак, имеем уравнение

. (*)

Найдем сначала определитель и определим тип кривой. Пусть оказалось, что имеем центральную кривую эллиптического или гиперболического типа. Тогда:

1. Находим центр кривой из системы уравнений

.

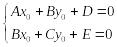2. Переносим начало координат параллельным сдвигом осей в точку , обозначим новые координаты точек .

Рисунок 8

Очевидно, , откуда , . После подстановки в уравнение (*) вместо х, у их выражений через , получим уравнение

,

где . В результате квадратичная форма не изменится, а члены, содержащие первые степени переменных и , пропадут!

3. Далее следует произвести поворот координатных осей , вокруг начала на угол  (>0 – против часовой стрелки) так, чтобы в уравнении исчез смешанный член . Как найти угол , т.е. как направить новые координатные оси? Новые оси направим вдоль собственных векторов , квадратичной формы, найдем матрицу перехода С к новому базису, и преобразуя координаты в с помощью матрицы С, получим в новых координатах уравнение в каноническом виде:

,

где ₁, ₂ – собственные числа матрицы (см. умение 5 и соответствующий пример тренинга и рисунок 8).

Рассмотрим теперь случай, когда определитель , и мы имеем случай параболический, центра нет. Тогда следует действовать по плану:

1. Находим собственные числа ₁, ₂ (при этом одно из них равно нулю) и собственные векторы , квадратичной формы. Поворачиваем исходную координатную систему ХОУ вокруг начала (0,0), направляя новые координатные оси и по собственным векторам , . Новые координаты точек и старые (х,у) связаны формулами

,

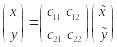где С – матрица перехода от исходного стандартного базиса к базису , .

2. После подстановки в уравнение (*) вместо х, у их выражений через получим или , где придется честно пересчитать.

3. Выделяя в полученном уравнении “полный квадрат” (см. юниту по аналитической геометрии), найдем вершину параболы . Перенесем начало координат в вершину параболы с помощью параллельного сдвига осей и . В новых координатах , где

получим каноническое уравнение параболы или .