2 Приведение симметричной матрицы к диагональному виду
2.1 Скалярное произведение в пространстве Rn. Процесс ортогонализации
В юните 1 нашего курса уже было введено понятие скалярного произведения в пространстве Rn. Напомним его.
Пусть
и
– два вектора пространства Rn,
тогда скалярным произведением
векторов
и
называется число
:
,
или
.
В следующих главах будет обобщено понятие скалярного произведения и рассмотрены его основные свойства.
Здесь напомним, что длина вектора (норма вектора)
.
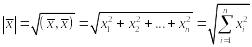Два вектора
и
ортогональны, если их скалярное
произведение равно нулю, т.е.
.
Определение. Система
векторов
,
в Rn
ортогональна, если
1)
,
для всех
;
2)
,
для всех
.
Можно доказать (что будет сделано ниже), что ортогональная система линейно независима.
Определение. Ортонормированной называется система векторов , из Rn, если
1) система ортогональна;
2) длина каждого вектора системы равна
1, т.е.
,
.
Любой вектор
можно нормировать, т.е. построить
такой вектор
,
что
.
Вектор называется ортом вектора , если его длина равна единице, а его координаты:
.
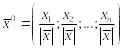Например, ортом вектора
является вектор
,
т.к.
.
Итак, всякую ортогональную систему легко превратить в ортонормированную.
Любая ортонормированная система из n векторов пространства образует ортонормированный базис пространства .
Пусть
линейно независимая система векторов
из
.
Тогда ее можно ортогонализовать,
т.е. построить ортогональную систему
векторов
такую что, линейные оболочки векторов
и
совпадают
.
О линейной оболочке см. юниту 1.
Покажем, как из системы строится система .
Алгоритм процесса ортогонализации:
1)
,
2)
,
коэффициент
подберем так, чтобы
и
были ортогональны, т.е.
.
,
отсюда
.
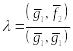3)
,
1
и
2
находим из условий:
и
,
или
,
так как
,
то
.
,
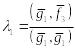так как
,
то
.
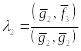Итак,
,
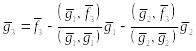или
.
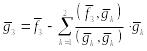Аналогично строятся векторы , где
.
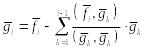Заметим, что векторы новой системы
являются линейными комбинациями векторов
линейно независимой системы
,
т.е. принадлежат
.
Итак, от произвольного базиса
линейной оболочки
мы перешли к ортогональному базису
,
причем
.
Пример. В пространстве
векторы
и
не коллинеарные и образуют базис. Так
как
,
то базис
не ортогональный. Построим ортогональный
базис
.
1.
.
2.
,
где
,
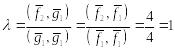(рисунок 4).
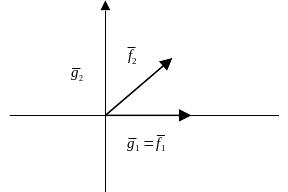
Рисунок 4
Базис – ортогональный, но не нормированный. Нормируем этот базис:
;
,
;
.
Базис
– ортонормированный стандартный базис.
Стандартные базисы
в
и
,
,...,
в
являются ортонормированными базисами.
2.2 Ортогональная матрица
Пусть
– базис в пространстве
,
а
– другой базис того же пространства.
Векторы
однозначно выражаются через базис
:
или
.
Запишем координаты вектора
по базису
в k-й столбец матрицы А:
.
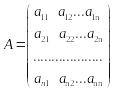Напомним, что эта матрица называется
матрицей перехода от базиса
к базису
.
Матрица А невырождена, так как ее
столбцы – координаты базисных векторов
,
следовательно существует обратная
матрица
,
которая является матрицей перехода от
базиса
к базису
.
Рассмотрим частный случай когда
и
два ортонормированных базиса в
и
.
Обозначим матрицу перехода U,
.
Матрица U обладает следующими
свойствами: ее вектор-столбцы
образуют ортонормированный базис в
,
т.е.
а)
,
б)
.
Определение.
Квадратная матрица порядка n,
столбцы которой удовлетворяют условиям
,
называется ортогональной.
Перечислим основные свойства ортогональной матрицы U:
1. Строки матрицы U (как и ее столбцы) образуют ортонормированный базис в .
2.
,
т.е. вычисление обратной матрицы для U
сводится к ее транспонированию.
3.
для всех
.
Это свойство означает, что скалярное произведение при действии ортогональной матрицы U на векторы сохраняется, а значит сохраняются длины векторов и углы между ними.
Любое из перечисленных свойств может служить определением ортогональной матрицы. Мы будем придерживаться первоначально данного определения.
Рассмотрим примеры.
1. В пространстве
поворот на угол
по часовой стрелке задается матрицей
перехода
.
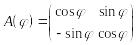Легко проверить, что матрица
ортогональна. Из геометрических
соображений очевидно, что длины векторов
и углы между ними при таком преобразовании
сохраняются.
2. В пространстве рассмотрим преобразование – отражение вектора относительно оси ОХ (рисунок 5).
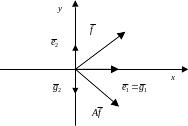
Рисунок 5
При таком преобразовании базис
перейдет в базис
,
.
Тогда, матрица перехода А от базиса
к базису
имеет вид:
.
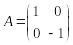Очевидно, это преобразование сохраняет длины векторов и углы между ними, а матрица перехода А ортогональна.
В заключение посмотрим, как меняются координаты вектора при переходе от одного базиса к другому.
Пусть в
заданы два базиса
и
.
Обозначим С матрицу перехода от
старого базиса
к новому базису
,
т.е.
,
.
Выберем произвольный вектор
,
разложим его по “старому” базису :
.
Аналогично, разложение этого вектора по “новому” базису имеет вид:
.
Зависимость между “старыми” координатами
и “новыми”
вытекает из следующей цепочки равенств:
.
Так как разложение вектора по базису единственно, то получаем
,
.
(*)
Обозначим векторы–столбцы старых и новых координат соответственно
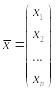и
,
,
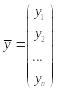тогда равенство (*) можно записать так:
.
(**)
Итак, чтобы получить координаты вектора
в “старом” базисе необходимо его
вектор–столбец “новых” координат
умножить слева на матрицу перехода из
старого базиса в новый. Так как матрица
С имеет обратную
,
то умножив равенство (**) слева на матрицу
,
получим выражение “новых” координат
через “старые”:
.
Пример. “Старый” базис в
пространстве
(на плоскости) –
“новый” базис
получен из “старого” поворотом на угол
по часовой стрелке (рисунок 6, 7). Матрица
перехода от базиса
к базису
.
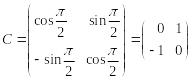Пусть вектор
в базисе
имеет координаты
.
Найдем координаты
в базисе
(рисунок 6, 7).
,
,
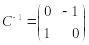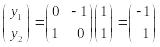т.е.
,
.
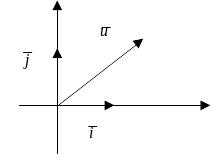
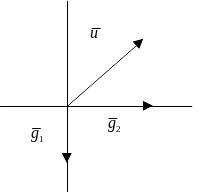
Рисунок 6 Рисунок 7