12 Пример выполнения упражнения тренинга на умение № 12
Задание 1
Определить матрицу оператора A в базисе {f}, если f1 = e1 – e2 + e3, f2 = – e1 + e2 – 2e3, f3 = 2e2 – e3; в базисе {e} матрица оператора равна
.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить матрицу перехода С от {e} к {f}. Вычислить С–1 |
|
2 |
Записать матрицу Ае оператора А в базисе {e} |
Матрица Ае задана
|
3 |
Вычислить матрицу оператора в базисе {f}:
|
|
Задание 2
В пространстве многочленов степени 2 задан оператор
D : p(t) 2p – p.
Найти матрицу оператора D в стандартном базисе e1 = 1, e2 = t, e3 = t2 и в базисе f1 = t2 + 1, f2 = t – 1, f3 = t.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Составить матрицу перехода от {e} к {f}. Вычислить С–1 |
f1 = t2 + 1 = e1 + e3 = (1, 0, 1), f2 = t – 1 = – e1 + e2 = (– 1, 1, 0), f3 = t = e2 = (0, 1, 0).
|
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
2 |
Записать матрицу Ае оператора D в базисе {e} |
D(e1) = 21 – 0 = 2 e1 = (2, 0, 0), D(e2) = 2 t–1 = – e1 + 2e2 = (– 1, 2, 0), D(e3) = 2t2 – 2t = –2e2 + 2e3 = (0, – 2, 2),
|
3 |
Вычислить матрицу Аf оператора D в базисе {f}: Аf = С–1 АеС |
|
Решите самостоятельно следующие задания:
Задание 12.1
Линейный оператор А в базисе {e} имеет матрицу
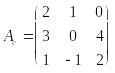
Найти матрицу этого оператора в базисе {f}, если f1 = 2e1 + 3e2 + e3; f2 = 3e1 + 4e2 + e3; f3 = e1 + 2e2 + 2e3.
Задание 12.2
В пространстве R3 оператор A : R3 R3, Ax = (2x1, x2, x3 + x1), где x = (x1, x2, x3) R3. Написать матрицу оператора Ae в стандартном базисе {e} и Af в базисе {f}, где f1 = e1 + e2 + e3; f2 = 4e2 + e3; f3 = e2 + 2e3.
Задание 12.3
В линейной оболочке L(et, e–t) задан оператор
D(f) : f(t)
2f –
.
Написать матрицу оператора D в базисах et, e–t и cht, sht.
13 Пример выполнения упражнения тренинга на умение № 13
Задание
В пространстве Р многочленов степени
≤ 2 задана система векторов f1
= t (t + 1), f2 = t, f3
= 1 и преобразование А : p(t)
t
.
Убедиться, что {f} – базис, оператор
А – линейный. Написать матрицы
оператора А в базисах {e} и {f},
где {e} – стандартный базис 1, t,
t2.
Решение
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
1 |
Выписать стандартный базис |
e1 = 1, e2 = t, e3 = t2, dim p = 3 |
2 |
Выяснить, образует ли система {f} базис |
Координаты векторов {f} в базисе {e}:
Найдем ранг системы векторов {f}
Ранг системы {f} равен dim p, f1, f2, f3 – базис пространства Р |
3 |
Проверить линейность оператора А |
Пусть f, g P – любые многочлены степени 2, , – произвольные числа, тогда A(f + g) = t(f + g) = tf + tg = A(f) + A(g); A – линейный оператор |
№ п/п |
Алгоритм |
Конкретное соответствие данного задания предложенному алгоритму |
4 |
Выписать матрицу перехода С от {e} к {f}. Вычислить С–1 |
Координаты векторов f1, f2, f3 по базису {e} (см. п. 2) запишем в столбцы матрицы С:
|
5 |
Написать матрицы оператора А в базисах {e} и {f} |
Применим преобразование А к базисным векторам {e}: Ae1 = 0 = 0e1 + 0e2 + 0e3 = (0, 0, 0), Ae2 = t = 0e1 + 1e2 + 0e3 = (0, 1, 0), Ae3 = 2t2 = 0e1 + 0e2 + 2e3 = (0, 0, 2),
Af1 = 2t2 + t = 2(t2 + t) – t = 2f1 – f2 = (2, – 1, 0), Af2 = t = f2 = (0, 1, 0), Af3 = 0 = (0, 0, 0),
|
6 |
Убедиться, что
|
|
.
,
Решите самостоятельно следующие задания:
Задание 13.1
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = t; f2 = 1 + t2; f3 = 1 – t2; A(p) = p + p.
Задание 13.2
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = (1 +t2); f2 = 1 + t; f3 = 1; A(p) = 2p – p.
Задание 13.3
В пространстве многочленов степени 2 задана система векторов {f} и преобразование А. Убедиться, что {f} – базис, оператор А – линейный. Написать матрицы оператора А в базисе {f} и в стандартном базисе {e}.
f1 = (t2 – 1); f2 = t; f3 = t + 1; A(p) = t p.
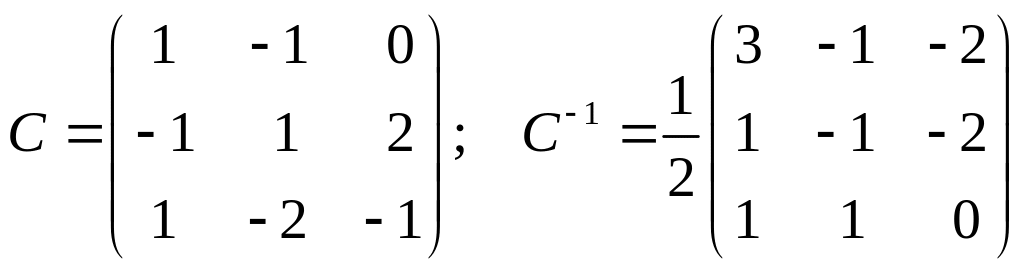
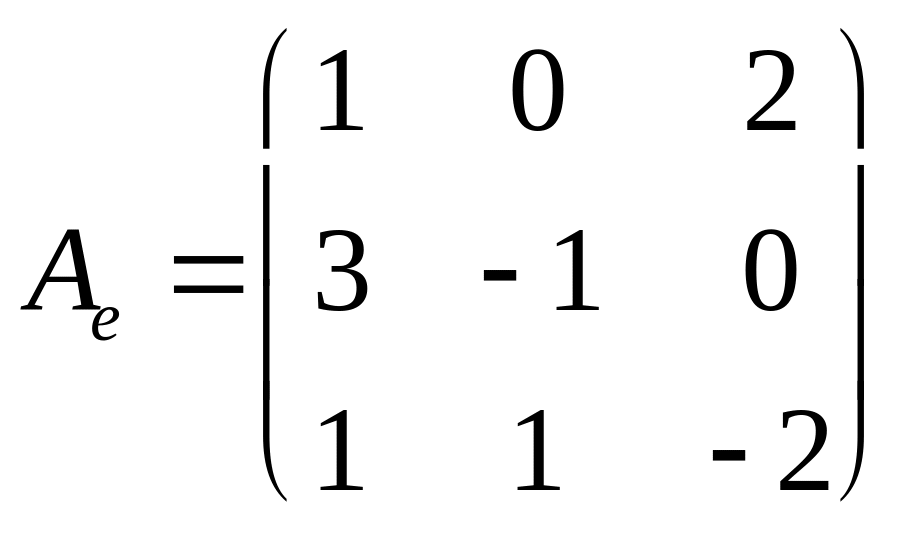
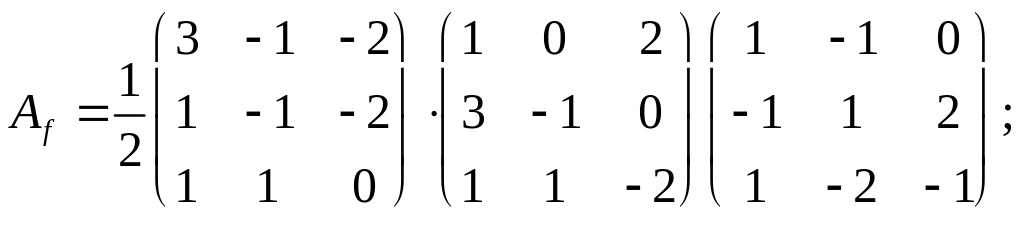
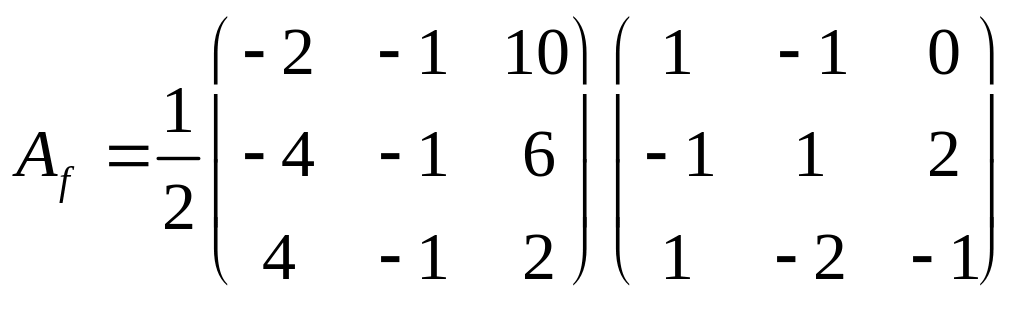
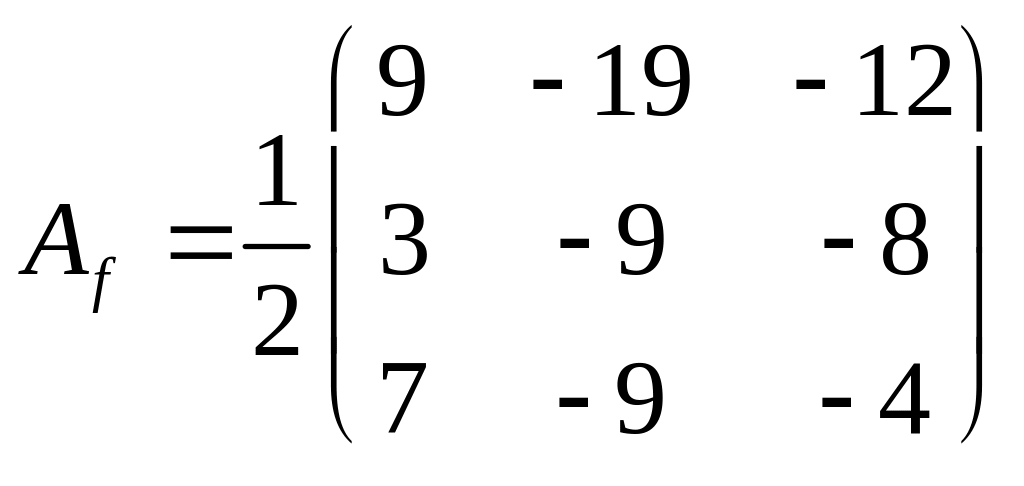
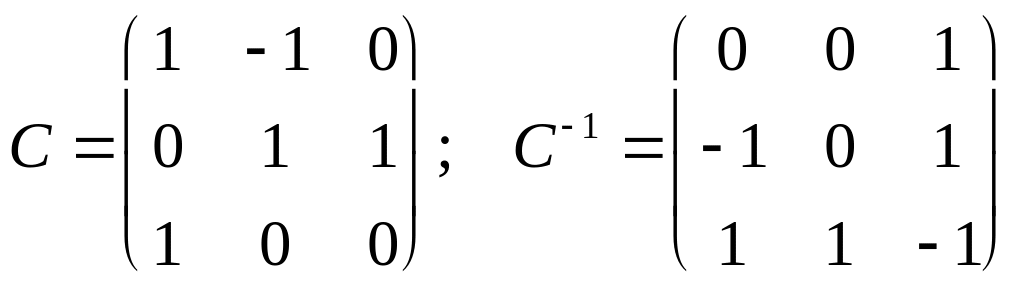
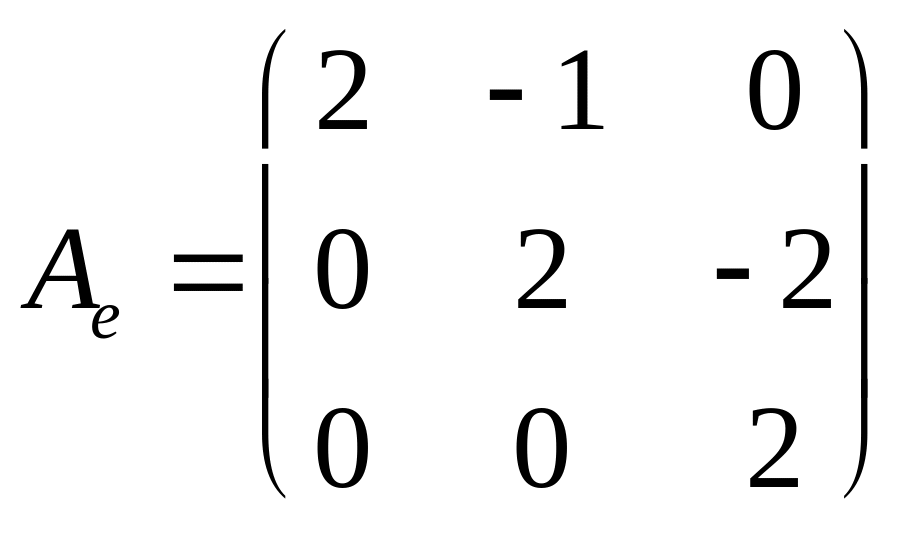
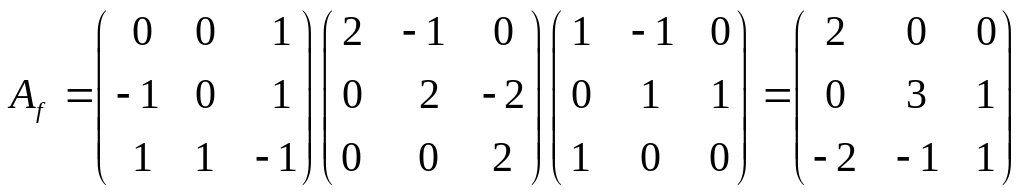
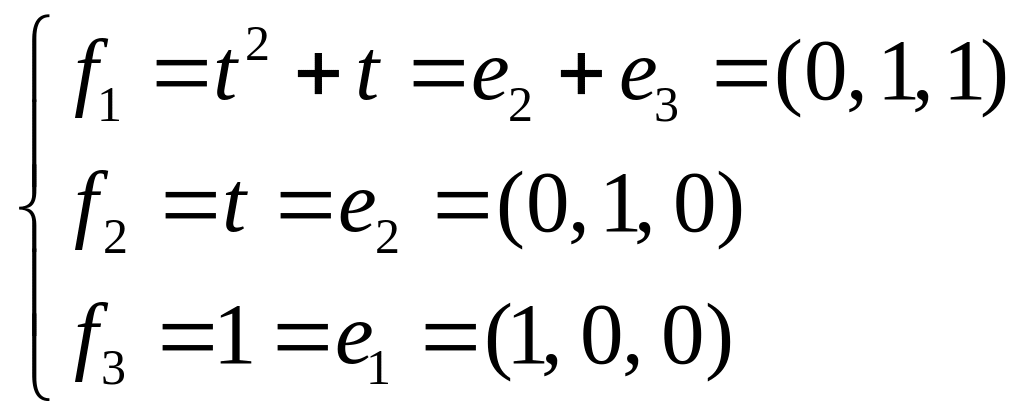
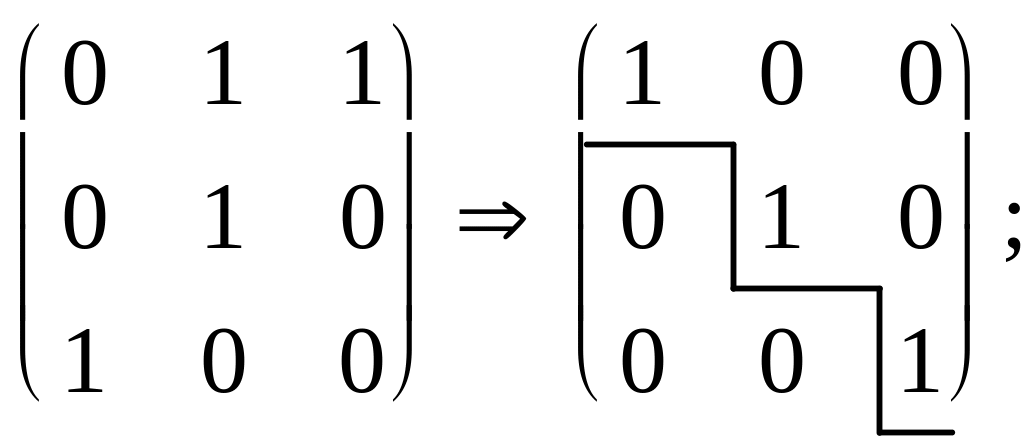
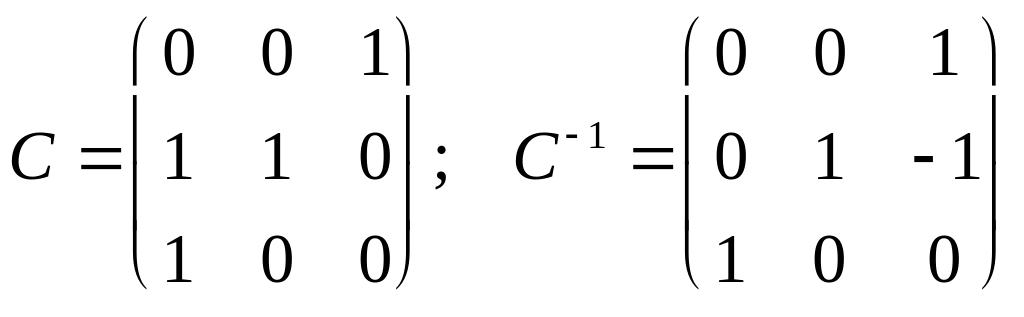
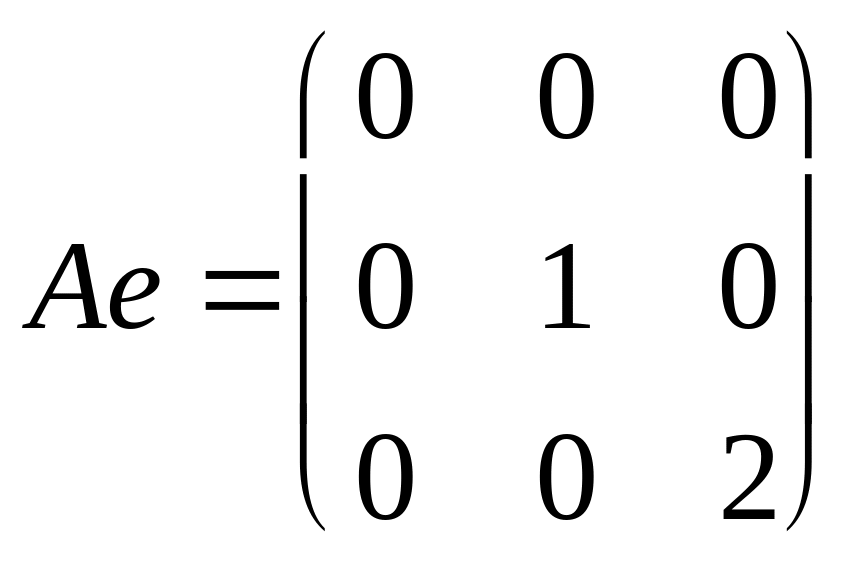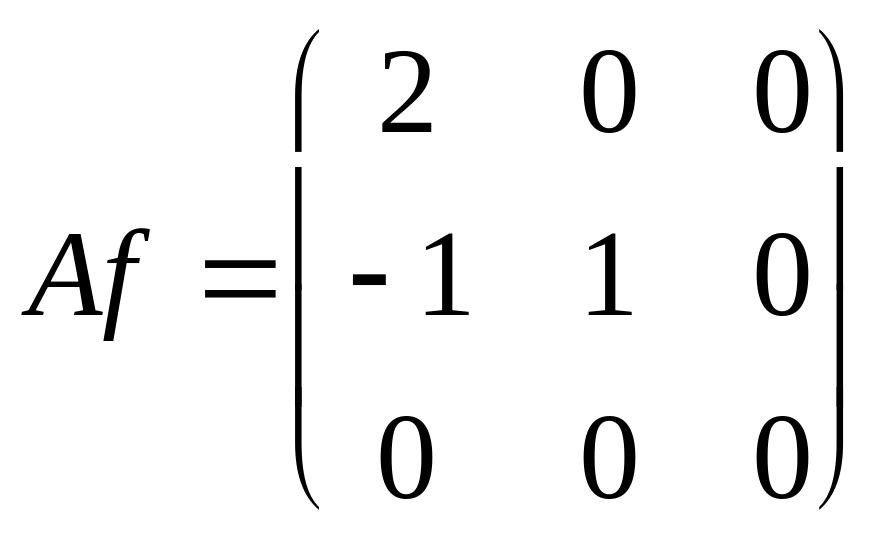
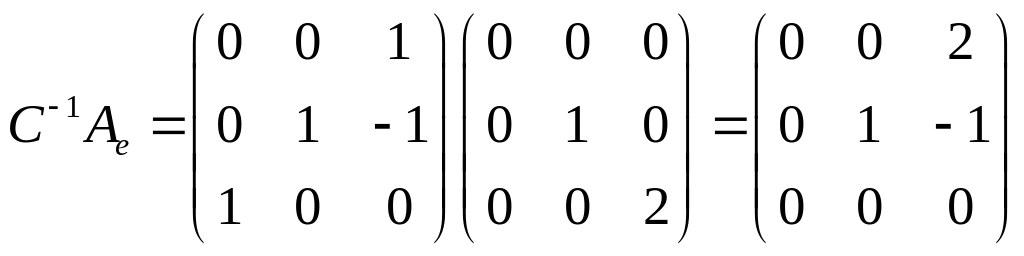