5 Линейные операторы
5.1 Определение и примеры
Пусть имеется линейное пространство V.
Определение. Линейным оператором
(линейным преобразованием) в линейном
пространстве V называется правило,
по которому каждому вектору
ставится в соответствие вектор
,
причем выполняются условия линейности:
1.
.
2.
,
– вещественное число.
Откуда по индукции получаем
.
Вектор
называют образом вектора х,
а х – прообразом вектора у.
Оператор представляет собой обобщение
понятия функции, когда область определения
и область значений функции
принадлежат линейному пространству V.
Обозначение
напоминает обозначение функции,
где аргументом является вектор х;
оператор А, действующий в пространстве
V, обозначают:
и называют преобразованием пространства.
Непосредственно из определения вытекает,
что
.
Примеры линейных операторов.
1. Нулевой оператор: каждому вектору ставится в соответствие 0-вектор из V –
.
2. Тождественный оператор: каждому вектору ставится в соответствие сам вектор х
.
3. Оператор подобия:
,
где – некоторое действительное число.
4. В пространстве рассмотрим подпространство многочленов степени . На этом подпространстве определим оператор дифференцирования D:
,
.
Линейность оператора D следует из линейности операции дифференцирования.
5. В пространстве
задана фиксированная функция
;
– произвольная функция из
.
Оператор
определим так:
– оператор умножения на фиксированную
функцию.
Легко проверяется его линейность:
,
где
;
– вещественные числа.
6. В пространстве
векторов на плоскости (все векторы
выходят из начала координат) рассмотрим
преобразование
– поворот плоскости на угол против
часовой стрелки.
На рисунке 9 показано преобразование
поворота на угол
против часовой стрелки. Очевидно, что
при повороте векторов
и
на этот угол диагональ параллелограмма
(их сумма) поворачивается на тот же угол,
т.е.
.
Так же очевидно, что операции умножения
вектора на число и поворот на угол
можно выполнить в обратном порядке –
результат получим тот же. Следовательно,
это преобразование линейное.
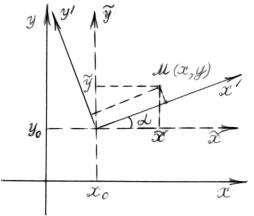
Рисунок 9
5.2 Матрица линейного оператора
Пусть в пространстве V выбран
некоторый базис
.
Линейный оператор А полностью
определится своим действием на векторы
базиса
.
Действительно, любой вектор
можно представить в виде
.
Пусть А – некоторый линейный
оператор, действующий в пространстве
V, тогда
.
Векторы
не зависят от х, а зависят только от
базиса и преобразования А. Каждый
из векторов
можно разложить по базису
(как и любой вектор пространства V)
.
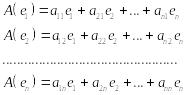Запишем координаты вектора по базису в i-й столбец матрицы А.
.
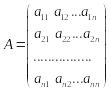Таким образом, если задано линейное
преобразование
и в пространстве V выбран
некоторый базис
,
то линейному оператору А отвечает
некоторая квадратная матрица А
порядка n, столбцами которой служат
координаты векторов
.
Эта матрица называется матрицей
линейного оператора А в
базисе
.
Обозначать матрицу оператора А мы
будем той же буквой
А,
или
,
чтобы подчеркнуть, что матрица оператора
зависит от выбора базиса.
Найдем теперь координаты вектора
.
Сравнивая коэффициенты
при базисных векторах
,получим
,
.
Таким образом, координаты вектора-образа линейно выражаются через координаты прообраза х и матрицу оператора А:
.
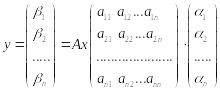Эту запись будем называть матричной формой записи линейного оператора в базисе .
Рассмотрим несколько примеров.
1. Матрица тождественного (единичного)
оператора
в любом базисе имеет вид:
.
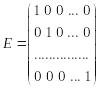Так как ее i-й столбец
(1 стоит на i-м месте).
2. Матрица оператора подобия (диагонального оператора) имеет вид:
.
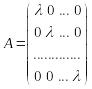3. Пусть V – пространство многочленов
от х степени
.
Найдем матрицу оператора дифференцирования
в базисе
,
,
,
…,
.
,
,
,
,
.
Матрица оператора D в этом базисе
имеет вид:
.
Сменим базис и
найдем матрицу того же оператора
дифференцирования D
в базисе
:
,
,
,
,…,
.
,
,
,
,
.
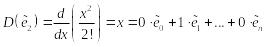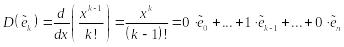Матрица оператора в базисе
имеет вид:
.
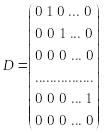4. Рассмотрим в евклидовом пространстве
оператор
,
,
где
– стандартный базис,
,
т.е. Р – оператор проектирования на
линейную оболочку
.
Для каждого базисного вектора
,
,
имеем
(единица стоит на k-м месте). Если же
,
то
.
Тогда матрица оператора Р:
.
Так, если
проектирует трехмерный вектор на
плоскость ХОУ, то
,
,
,
а матрица
.
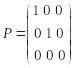5. Матрица оператора поворота плоскости на угол против часовой стрелки в стандартном базисе :
–
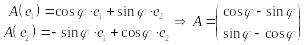уже знакомая нам ортогональная матрица.
Итак, каждому линейному оператору , где V – n-мерное пространство, в заданном базисе соответствует квадратная матрица n-го порядка. Покажем, что такое соответствие является взаимнооднозначным, т.е. каждой квадратной матрице порядка n отвечает некоторое линейное преобразование в заданном базисе.
Пусть в пространстве
V
выбран некоторый базис
и задана
квадратная матрица А
порядка n.
Пусть
.
Поставим в соответствие вектору х
вектор
такой, что
,
т.е.
,
здесь
и
координаты прообраза х и образа у
в базисе
.
Так заданный оператор является линейным (легко проверяется). Найдем матрицу построенного оператора, пользуясь введенным правилом.
,
,
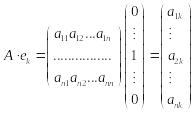т.е. матрица совпадает с заданной матрицей А. Значит каждая квадратная матрица является матрицей некоторого линейного оператора. Итак, выбор базиса в n-мерном пространстве V устанавливает взаимно однозначное соответствие между линейными операторами, действующими в этом пространстве и квадратными матрицами порядка n.
Как уже говорилось, матрица оператора зависит от выбранного в пространстве базиса. Определим, как меняется матрица оператора с изменением базиса. Связь старого (исходного) базиса и нового задается матрицей перехода С. Следующая теорема устанавливает связь между матрицами одного и того же линейного оператора в различных базисах.
Теорема. Пусть
и
два базиса в n-мерном линейном
пространстве V, С – матрица
перехода от
к
,
и
– матрицы оператора А в этих базисах.
Тогда
.
Доказательство.
Обозначим вектор-столбцы координат
векторов
в базисах
и
соответственно
.
Напомним, что
,
.
Пусть теперь
,
.
Выразим матрицу
оператора в базисе
через матрицу перехода С и матрицу
оператора в базисе
:
;
.
Сравнивая результаты, получим:
.
Матрицы А и В подобны, если
существует невырожденная матрица Р,
что
;
тогда
.
Итак, матрицы оператора и в различных базисах подобны, и определитель матрицы оператора не зависит от выбора базиса.
Пример. В пространстве
матрицы оператора в стандартном базисе
,
имеет вид:
.
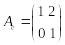Найти матрицу того же преобразования
в базисе
и
.
Решение. Заметим, что
линейно независимы и образуют новый
базис в
.
Выпишем матрицу перехода от
к
,
для чего запишем координаты векторов
в стандартном базисе в столбцы матрицы
С
.
,
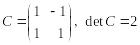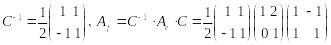откуда
.
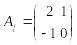Покажем, как по другому можно получить ту же матрицу .
Координаты и матрица оператора задана в стандартном базисе. Найдем образы и в том же базисе :
;
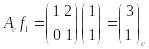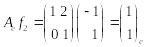или
;
.
(*)
Нам надо получить выражения образов
и
в базисе
.
.
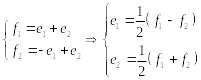Подставляя выражения
и
через
и
в равенства (*), получаем
,
.
Выписывая по столбцам координаты образов
и
в базисе
,
получаем
.
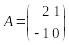