4.3 Базис и координаты. Размерность пространства

Понятие базиса пространства Rⁿ уже обсуждалось ранее. Аналогично определяется базис любого линейного пространства.

Определение. Конечная система векторов называется базисом линейного пространства V, если:

а) векторы линейно независимы;

б) любой вектор пространства V представляется в виде линейной комбинации векторов базиса:

. (*)

Коэффициенты разложения (*) определяются однозначно и называются координатами вектора в базисе . Действительно, в противном случае, если и , где для некоторых , то вычитая почленно получим , нулевую линейную комбинацию векторов , где не все коэффициенты равны нулю. Это противоречит условию линейной независимости системы {f}.

Из единственности разложения следует что два вектора равны, если совпадают их координаты по любому базису.

Примеры.

1. В пространстве тройка векторов представляют базис, а координатами любого вектора по этому базису являются проекции вектора на координатные оси.

2. Стандартным базисом в пространстве Rⁿ служит система линейно независимых векторов ; , …, и каждый вектор , .

3. В пространстве многочленов степени функции образуют базис. Линейная независимость этой системы уже проверялась. Координаты любого многочлена по данному базису равны . Введение базиса позволяет перейти от линейных операций над векторами линейного пространства к операциям над их координатами, т.е. к привычным операциям над числами.

Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все координаты его умножаются на то же число.

Перейдем к понятию размерности пространства.

Изучая аналитическую геометрию, мы заметили, что на прямой не существует двух линейно независимых векторов; на плоскости любая пара неколлинеарных векторов линейно независима, но каждые три вектора уже линейно зависимы; в пространстве же существуют линейно независимые тройки векторов (неколлинеарных), но уже любые четыре вектора линейно зависимы. Упомянутые пространства отличаются своей размерностью.

При изучении пространства Rⁿ (юнита 1) мы убедились, что в пространстве можно выбрать различные базисы. Все они обладают важным свойством – число их векторов одинаково.

Это свойство справедливо для любого линейного пространства V.

Определение. Число векторов во всех базисах пространства V одинаково. Это число называется размерностью пространства V и обозначается .

Если , то любые n линейно независимых векторов пространства V образуют базис. Поэтому прямая линия – одномерное пространство, плоскость – двумерна, а привычное нам пространство – трехмерно.

Если в пространстве можно выбрать любое число линейно независимых векторов, то его называют бесконечномерным.

В пространстве многочленов степени не выше n есть базис из векторов, потому размерность этого пространства равна . Пространство же всех непрерывных на отрезке функции не является конечномерным. Мы будем рассматривать пространства, имеющие конечные базисы.

Пример 1. В пространстве рассмотрим два базиса. Базис : , (неколлинеарные) и : , . Найдем координаты вектора в каждом базисе. Очевидно, вектор , значит его координаты в базисе . В то же время , а значит .

Пример 2. Рассмотрим совокупность всех квадратных матриц 2-го порядка 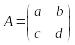. Как уже говорилось, они образуют линейное пространство. Покажем, что его размерность равна 4. Действительно, система матриц 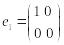, , 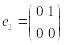, 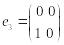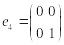линейно независима, а матрица – линейная комбинация . Система матриц – базис пространства, числа – координаты матрицы А в этом базисе. Базис состоит из 4 элементов, следовательно, пространство четырехмерно. Заметим, что пространство квадратных матриц порядка n имеет размерность .

Пример 3. В пространстве V многочленов степени , функции , , образуют базис.

Проверим их линейную независимость

,

.

.

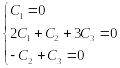Отсюда следует: .

Мы показали, что размерность пространства V многочленов степени равна 3, потому – базис пространства V.

Найдем координаты многочлена в базисе .

или

.

Сравнивая коэффициенты при одинаковых степенях х в многочлене слева и справа, получаем

.

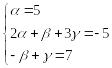Отсюда, , , – координаты многочлена в базисе : . Заметим, что в стандартном базисе многочлен имеет координаты .