4.2 Линейная зависимость

Пусть векторы из линейного пространства V; – действительные числа. Вектор называют линейной комбинацией .

Очевидно, при , . Но может быть, что линейная комбинация y=0, хотя не все коэффициенты c_i обращаются в нуль. Тогда говорят, что линейно зависимы.

Определение. Векторы называют линейно зависимыми, если существуют числа , не все равные нулю и такие, что

. (*)

Если же равенство (*) возможно только при , то – линейно независимы. Например, на плоскости два вектора и линейно зависимы тогда и только тогда, когда и коллинеарны. В пространстве же линейная независимость векторов эквивалентна их некомпланарности.

Как было показано (юнита 1), система векторов

из арифметического пространства Rⁿ линейно независима.

Рассмотрим несколько примеров линейно независимых систем векторов в пространстве – непрерывно дифференцируемых функций на отрезке .

Пример 1. Пара функций , линейно независимы на любом отрезке . Действительно, составим линейную комбинацию, приравняем ее 0-вектору пространства . Нулевым элементом этого пространства является функция, принимающая значение нуль во всех точках отрезка , т.е. (отрезок оси ОХ).

.

Это равенство должно выполняться для всех х из . Пусть х=0 сначала, затем положим (считаем, что 0 и принадлежат ), получаем:

,

.

Условие линейной независимости выполнено.

Система же функций в том же пространстве , , – линейно зависима, т.к. имеет место тождество , здесь , , .

Пример 2. Рассмотрим пространство многочленов степени . Система функций 1; х; ; линейно независима.

Составим их линейную комбинацию, приравняем нуль – вектору и найдем коэффициенты , , , :

.

Продифференцируем последовательно три раза последнее равенство, учитывая, что производные нуль-функции равны нулю тождественно, получаем

.

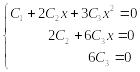Отсюда получаем .

Заметим, что вообще система функций линейно независима в пространстве многочленов степени , при любом

Отсюда следует, что многочлен степени n тождественно равен нулю тогда и только тогда, когда все его коэффициенты равны нулю, а два многочлена степени n равны, если совпадают их коэффициенты при одинаковых степенях х.

В дальнейшем мы познакомимся и с другими линейно независимыми системами в .

Лемма 1. Если среди векторов имеются линейно зависимые, то и вся система линейно зависима.

Действительно, если линейно зависимая подсистема, то существует нетривиальная линейная комбинация из этих векторов равная нуль-вектору:

(не все С_i равны нулю). (*)

Тогда приписав к (*) остальные векторы системы с нулевыми коэффициентами, получим

(**)

и линейная комбинация (**) тоже нетривиальна. Таким образом всякая подсистема линейно независимой системы векторов линейно независима.

Лемма 2. Вектора линейно зависимы тогда и только тогда, когда хотя бы один из них есть линейная комбинация других. Доказательство очевидно сразу же следует из определения линейной зависимости.

Лемма 3. Если в систему векторов входит 0-вектор, то она линейно зависима, так как существует, например, линейная комбинация , где С – любое, .