1.4. Установившееся движение сплошной среды

Установившимся или стационарным движением сплошной среды называется такое движение, в котором все параметры, характеризующие среду, не зависят от времени, т.е. в каждой точке пространства остаются постоянными.

Используя понятие локальной производной, можно сказать, что установившимся движением сплошной среды называется такое движение, в котором локальная производная от любого параметра по времени равна нулю.

, (1.8)

где А — произвольный параметр сплошной среды.

Следует отметить, что стационарность движения вовсе не предполагает, что параметры, характеризующие это движение, не изменяются вообще. Они остаются неизменными в каждой точке пространства, однако в разных точках пространства они могут отличаться друг от друга.

Пусть, например, нефть, нагретую для снижения ее вязкости, нагнетают в трубопровод. По мере движения нефть остывает, отдавая тепло в окружающую среду. В каждом сечении трубопровода температура нефти со временем не изменяется, т.е. , т.е. рассматриваемый процесс – установившийся, однако, от сечения к сечению температура нефти уменьшается. В этом случае скорость изменения температуры у каждой отдельно взятой частицы определяется только конвективными членами, т.е. в случае стационарного течения полная производная по времени представляется выражением

. (1.9)

Ускорение частиц сплошной среды

Используя понятия полной и локальной производной по времени, вводят ускорение частиц сплошной среды. Вектор ускорения точек сплошной среды определяется как полная производная по времени от скорости фиксированных частиц:

. (1.10)

В проекциях на координатные оси OX, OY, OZ векторное равенство (1.10) равносильно трем скалярным равенствам:

(1.11)

В частности, при одномерном движении сплошной среды, например, в направлении оси OX, ускорение имеет вид:

, (1.12)

а для установившегося режима:

. (1.13)

1.5. Закон сохранения массы. Уравнение неразрывности

Плотность и компоненты вектора скорости не могут быть произвольными величинами; сплошная среда должна двигаться так, чтобы выполнялся фундаментальный закон физики – закон сохранения массы. Как бы ни двигалась сплошная среда, но масса не должна ни появляться, ни исчезать.

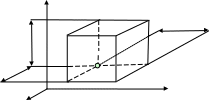
Рассмотрим фиксированный объем пространства, взяв его в виде малого параллелепипеда с гранями, параллельными координатным плоскостям, и ребрами с длиной , и (рис.1.4). Тогда одна из возможных формулировок закона сохранения массы сплошной среды состоит в следующем: изменение массы среды в рассматриваемом объеме за некоторый интервал времени должно равняться массе среды, втекающей за в этот объем через его поверхность (вытекающую среду будем считать втекающей со знаком минус).

Рис. 1.4. К выводу закона сохранения массы

Масса сплошной среды в малом объеме равна , а ее изменение за время выражается равенством

;

Масса сплошной среды, втекающей за время в рассматриваемый параллелепипед через переднюю и заднюю боковые грани (т.е. грани, параллельные плоскости на расстоянии друг от друга), может быть представлена равенством

Аналогично, массы и втекающие через боковые грани параллелепипеда в направлении осей и , представляются, соответственно, выражениями:

,

Отсюда следует, что суммарная масса сплошной среды, втекающей в параллелепипед через все шесть его граней, представляется выражением

Сравнивая выражения для , полученные в первом и втором пунктах, получаем дифференциальное уравнение

или

, (1.14)

называемое уравнением неразрывности. Это уравнение, как следует из метода его получения, выражает закон сохранения массы движущейся среды.

Если в (1.14) выполнить дифференцирование по частям, то получим другую форму записи уравнения неразрывности:

или, согласно (1.9):

.

Отсюда имеем:

. (1.15)

Сумма трех частных производных от компонент вектора скорости называют дивергенцией вектора и обозначают :

.

Дивергенция вектора скорости показывает относительное изменение плотности сплошной среды. Итак:

(1.16)