Глава 4

4. УРАВНЕНИЯ ДИНАМИКИ ЖИДКОСТИ

В ИНТЕГРАЛЬНОЙ ФОРМЕ

4.1. Применение основных теорем механики системы

материальных точек к подвижному объему жидкости.

Рассмотрим подвижный объем жидкости, ограниченный замкнутой поверхностью . С течением времени частицы жидкости, составляющие этот объем, перемещаются в пространстве, обуславливая изменение формы ограничивающей их поверхности. Подвижный объем жидкости, состоящий из одних и тех же частиц, называют индивидуальным объемом. Этот объем представляет собой тело, к которому применимы основные законы механики и термодинамики.

Интегральные характеристики индивидуального объема жидкости

На рис. 4.1 изображен индивидуальный объем жидкости, ограниченный замкнутой поверхностью .

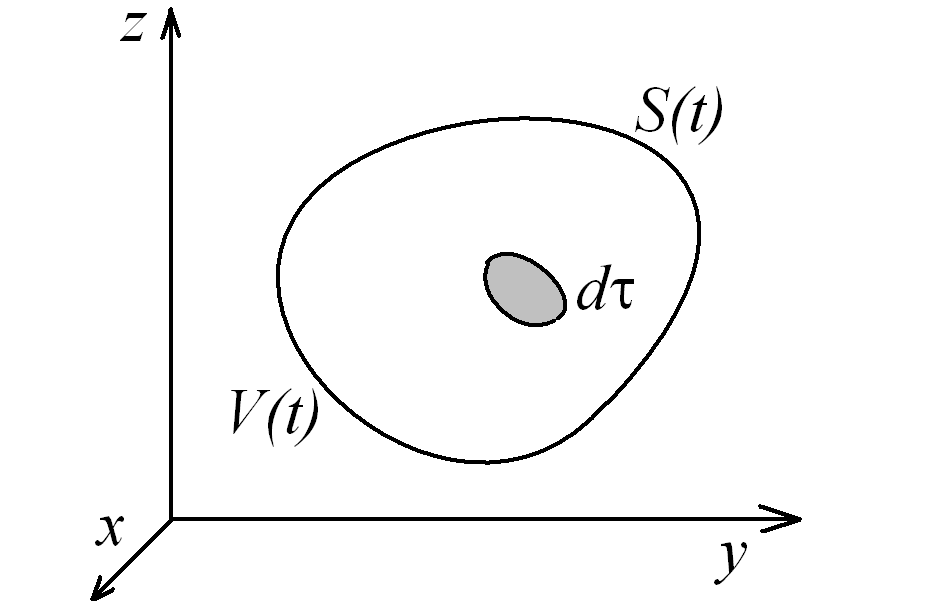
Рис. 4.1. Подвижный (индивидуальный) объем жидкости

Если обозначить элементарный объем пространства, занятого жидкостью, то его масса, количество движения, момент количества движения; кинетическая энергия, полная энергия, внутренняя энергия. Интегральные характеристики системы частиц жидкости, составляющих индивидуальный объем , определятся выражениями:

- масса объема;

- количество движения объема;

- момент количества движения объема;

- кинетическая энергия объема;

- внутренняя энергия объема;

- полная энергия объема.

Основные теоремы механики и термодинамики системы материальных точек могут быть представлены следующими равенствами.

а) Закон сохранения массы:

; (4.1)

б) Закон изменения количества движения:

, (4.2)

где — сумма всех внешних сил, приложенных к частицам подвижного объема , как массовых, так и поверхностных;

в) Закон изменения момента количества движения:

, (4.3)

где радиус-вектор рассматрвамой точки объема; сумма моментов всех внешних сил, действующих на частицы жидкости в рассматриваемом объеме.

г) Закон изменения кинетической энергии (теорема «живых сил»):

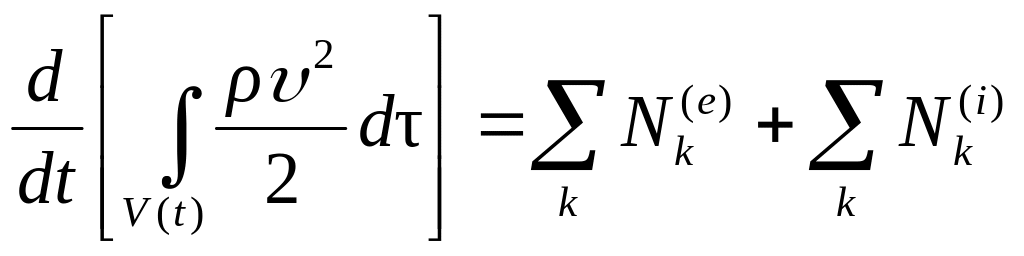, (4.4)

где и — суммы мощностей всех внешних и внутренних сил, приложенных к точкам рассматриваемого объема.

д) Закон изменения полной энергии (первый закон термодинамики)

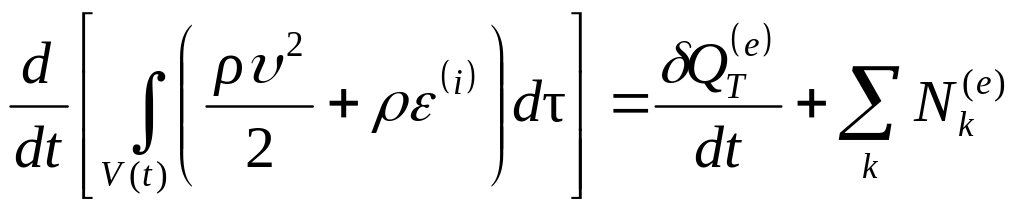, (4.5)

где приток внешней энергии в виде тепла; мощность всех внешних сил.

Эти законы справедливы не только для жидкости, но и вообще для любой сплошной среды. В общем виде соотношения (4.1) - (4.5) можно записать посредством уравнения

, (4.6)

в котором параметр может обозначать любую величину , , или , a обозначает правые части этих уравнений.

Полная производная по времени от интегральной характеристики индивидуального объема

Рассмотрим положение объема, состоящего из одних и тех же частиц, в два последовательных момента времени t и (рис.4.2). По определению полной производной можно записать

(4.7)

где объем пространства, занимаемый рассматриваемыми частицами в момент времени .

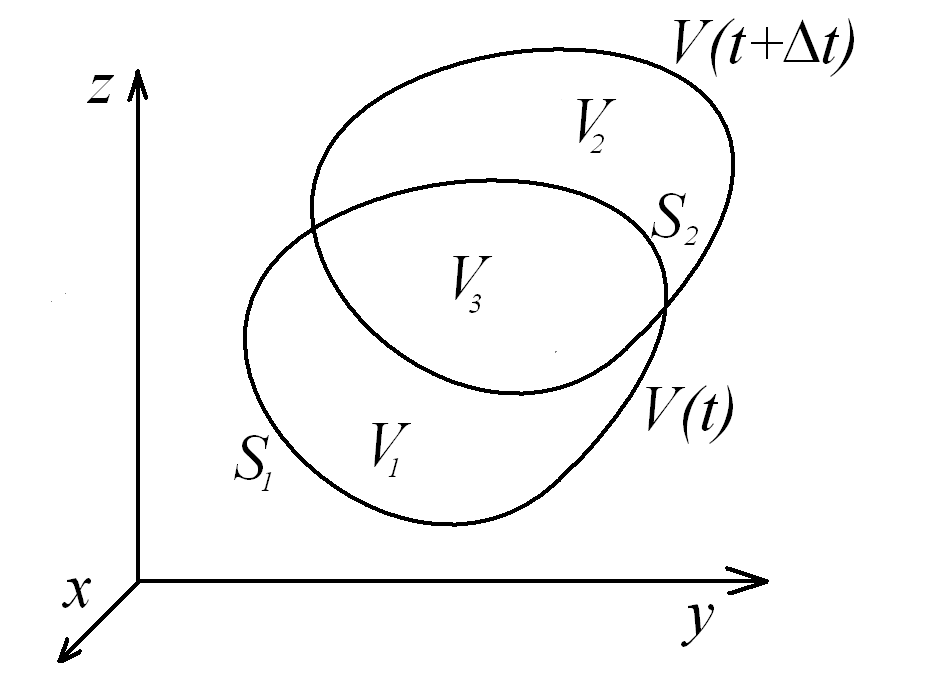
Рис. 4.2. Положение индивидуального объема жидкости в два последующие момента времени

Пусть объем общей части и , —объем части пространства вновь занятого частицами подвижного объема ( часть поверхности , через которую частицы выходят), объем части пространства, освобожденного частицами, подвижного объема ( часть поверхности S, через которую частицы входят). Тогда каждый из интегралов по объемам и в равенстве (4.7) можно разбить на две части

,

.

Подставляя это разбиение в формулу (4.7), получаем:

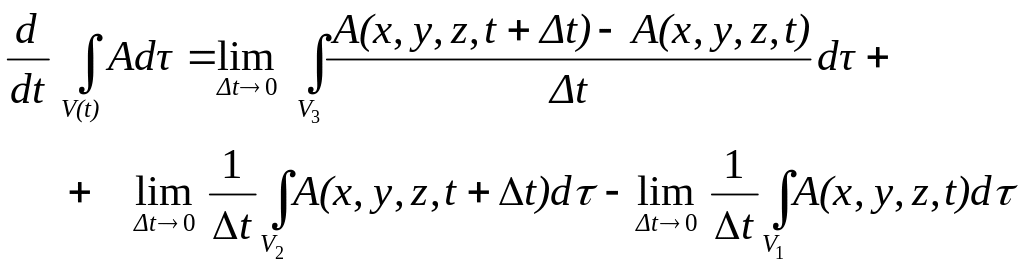. (4.8)

Первое слагаемое в правой части (4.8) равно интегралу от частной производной по времени величины :

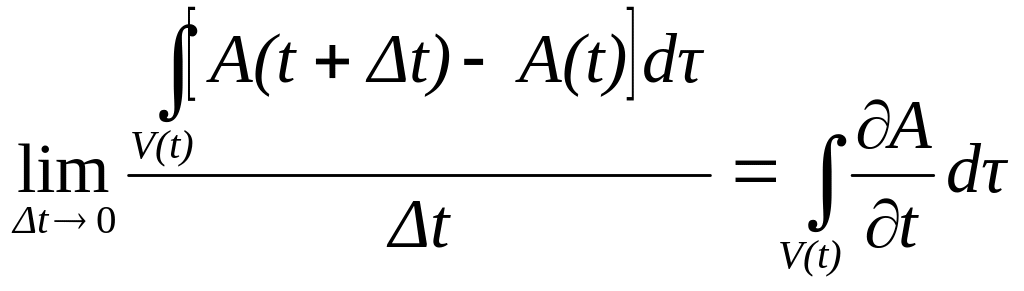. (4.9)

Второе и третье слагаемые можно преобразовать в интегралы по поверхности, ограничивающей подвижный объем.

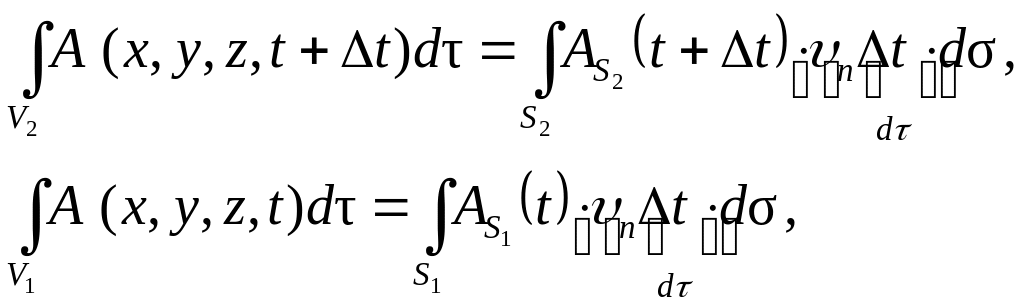(4.10)

где значения параметра в точках поверхности . Здесь было использовано представление элементарного объема в бесконечно тонком слое вокруг поверхностей и виде объема цилиндра с площадью основания (элемент поверхности) и образующей ( проекция вектора скорости частиц на нормаль к поверхности), (рис. 4.3).

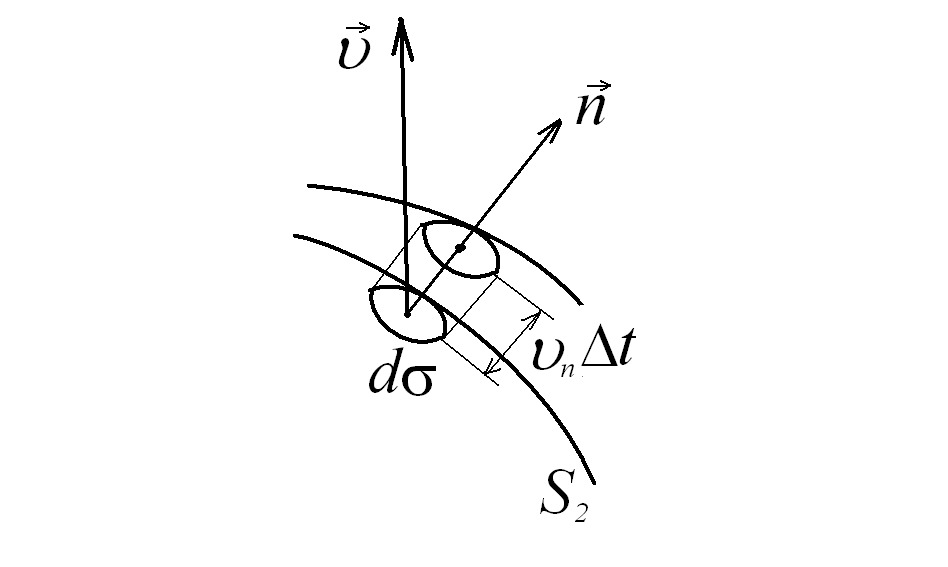
Рис. 4.3. Вычисление элементарного объема в точках

поверхности индивидуального объема

Подставляя (4.10) в (4.8) и переходя к пределу при , получаем:

. (4.11)

Здесь учтено, что для непрерывной функции имеет место равенство .