2.4. Силы, действующие со стороны жидкости на элементы поверхности тел, погруженных в жидкость

Формула (2.15) для распределения давления в покоящейся жидкости позволяет решить одну из фундаментальных задач гидростатики, дать ответ на вопрос о силовом действии со стороны жидкости на элементы поверхности тела, погруженного в жидкость.

Пусть криволинейный участок S (рис. 2.11) представляет элемент поверхности некоторого тела, погруженного в жидкость.

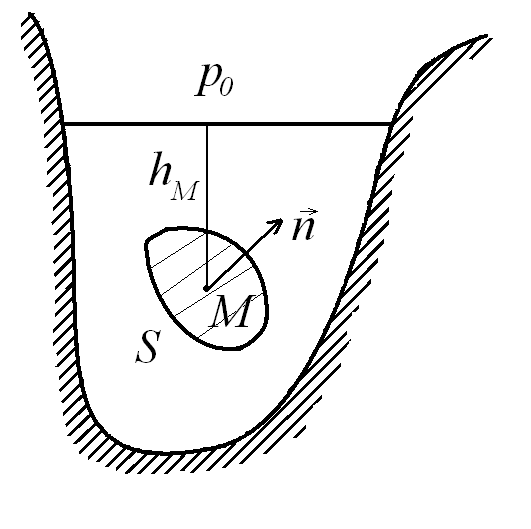
Рис. 2.11. Силы давления, действующие на элемент поверхности тела, погруженного в жидкость

Давление жидкости в точке М поверхности S за вычетом дополнительного давления столба воздуха на свободную поверхность , согласно (2.15) выражается равенством

, (2.17)

где — глубина точки М под свободной поверхностью.

Известно, что если некоторая система сил действует на твердое тело, то выбрав в этом теле некоторую точку О за полюс, можно все силы перенести в эту точку параллельным сдвигом, добавляя соответствующие пары сил. После этого оказывается, что система сил сводится к одной силе и к одной паре сил. Эта одна сила называется главным вектором сил давления жидкости на поверхность S. Его величина представляется интегралом

, (2.18)

где интегрирование происходит по поверхности . При переходе к другому полюсу главный вектор сил не изменяется.

Главный момент сил давления жидкости на стенку определяется равенством

, (2.19)

где — радиус-вектор произвольной точки поверхности пo отношению к точке О. При переходе от точки О к другому полюсу величина главного момента изменяется.

2.5. Сила давления жидкости на плоскую стенку

Рассмотрим действие жидкости на плоскую стенку. Под этим термином будем понимать случай, когда участок стенки лежит целиком в некоторой плоскости. Такие случаи встречаются в различных технических устройствах, например, в плоских затворах, закрывающих те или иные резервуары с жидкостью.

В случае плоской стенки, вектор нормали к поверхности, на которую воздействует жидкость, не изменяется и одинаков для всех точек стенки (рис. 2.12).

1. Вычислим главный вектор системы сил давления, являющейся в данном случае системой параллельных сил. Подставляя в формулу (2.18) выражение для давления (2.17), получаем:

. (2.20)

Здесь вектор был вынесен из-под знака интеграла благодаря тому, что он постоянный.

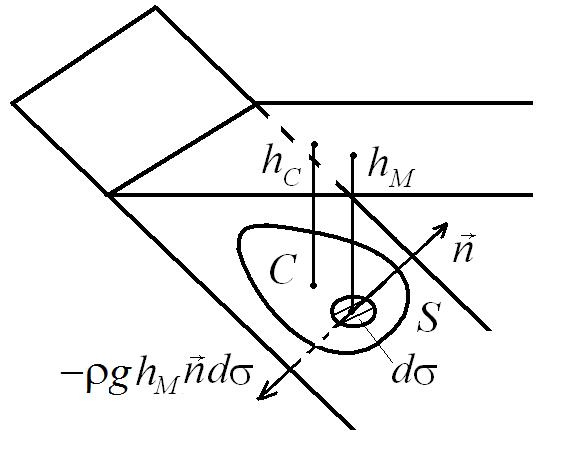
Рис. 2.12. Вычисление силы давления жидкости

на плоскую стенку

В математическом анализе используется понятие геометрического центра тяжести тела. Координаты геометрического центра тяжести определяются через статические моменты первого порядка. В частности, для плоской фигуры координаты геометрического центра тяжести определяются формулами

.

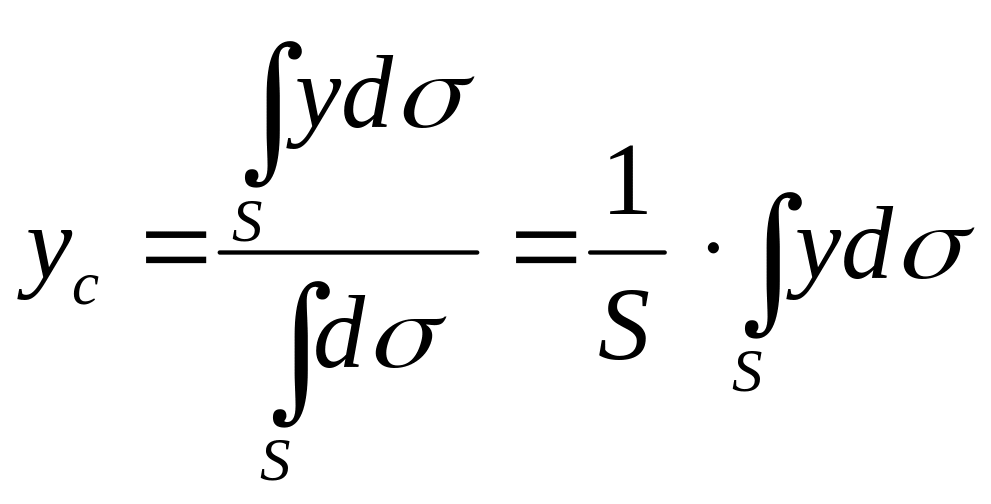Если речь идет о плоской фигуре в пространстве, то вертикальная координата геометрического центра тяжести определяется формулой

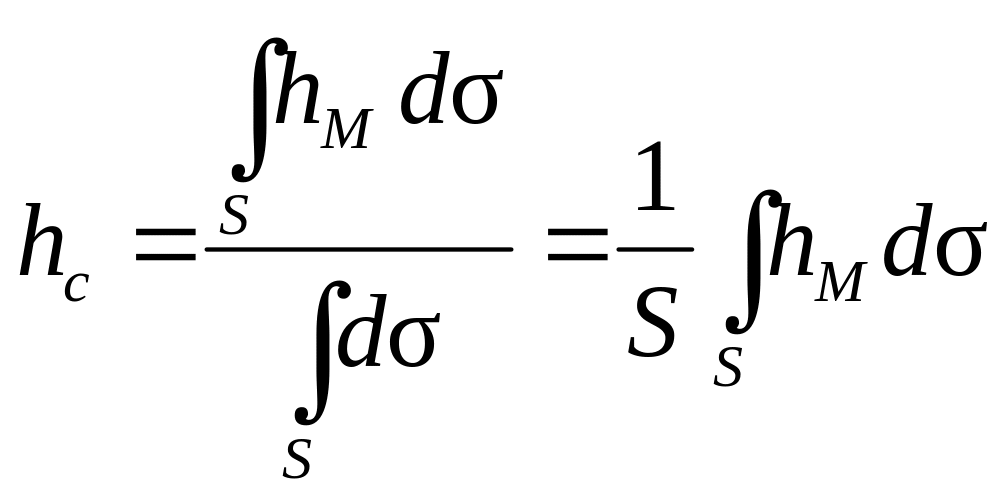(2.21)

поэтому формулу (2.20) для главного вектора сил давления можно представить в следующем виде:

. (2.22)

где глубина геометрического центра тяжести рассматриваемой плоской стенки под свободной поверхностью жидкости; площадь стенки.

Величина (модуль) главного вектора сил давления дается формулой

. (2.23)

Поскольку множитель равен избыточному давлению жидкости в геометрическом центре С тяжести стенки, то величина главного вектора сил давления равна произведению избыточного давления жидкости в центре тяжести стенки на площадь этой стенки.

. (2.24)

Направление главного вектора сил давления, как это следует из формулы (2.20), совпадает с направлением вектора , т.е. главный вектор сил давления направлен перпендикулярно стенке в сторону от жидкости. Учитывая, что произведения площади стенки на компоненты единичного вектора , равны площадям проекций стенки на плоскости, перпендикулярные осям координат OX, OY и OZ, соответственно, получаем:

(2.25)

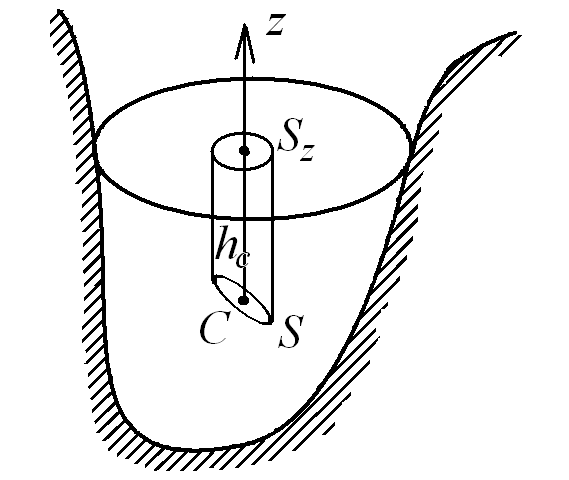
Рис. 2.13. Тело давления для элемента плоской поверхности

Величины и представляют горизонтальные составляющие вектора , a — ее вертикальную составляющую.

Смысл последнего равенства (2.25) особенно нагляден. Произведение представляет собой объем тела, заключенного между стенкой S, ее проекций на свободную поверхность и вертикальными проектирующими образующими (такое тело называется телом давления, рис. 2.13). Поэтому последняя формула означает, что вертикальная составляющая главного вектора сил давления жидкости на плоскую стенку равна по величине весу жидкости в объеме тела давления.

Найдём теперь точку приложения равнодействующей системы параллельных сил, действующих со стороны жидкости на стенку. Из нижеследующего будет видно, что эта точка не совпадает с центром тяжести С. Оказывается, что если все силы параллельным образом перенести в точку С, то кроме силы будет отличным от нуля и момент .

2. Вычислим главный момент сил давления. Для этой цели введем систему координат CXYZ, как показано на (рис. 2.14). Ось CY направим параллельно линии пересечения стенки и свободной поверхности, ось СХ вниз по стенке, ось CZ — в перпендикулярном направлении вниз. Начало системы координат выбираем в центре тяжести стенки, точке С. Обозначим угол наклона плоскости стенки к свободной поверхности через .

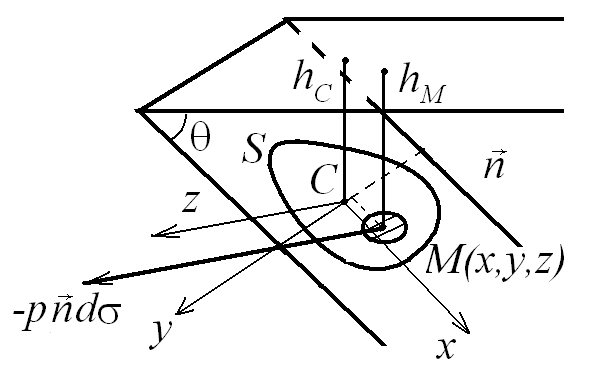
Рис. 2.14. Определение точки приложения сил давления

Если произвольная точка стенки , то ее глубина под свободной поверхностью жидкости и координата связаны равенством

. (2.26)

Очевидно, что главный момент системы параллельных (оси CZ) сил давления имеет проекции только на оси СХ и CY. Проекция на ось CZ равна нулю. Запишем выражения для проекций и вектора на оси выбранной системы отсчета. Проекция представляет собой сумму моментов действующих сил давления, составленных относительно оси СХ:

.

Подставляя сюда выражение для давления и учитывая (2.26), получаем:

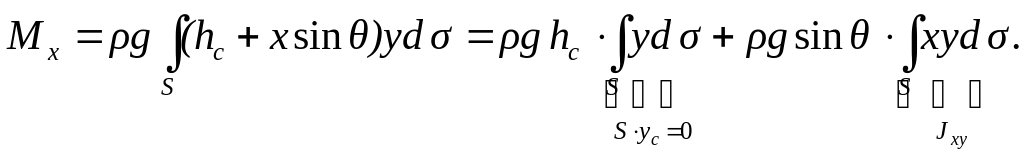
Первое слагаемое в правой части последней формулы равно нулю, поскольку координата центра тяжести в выбранной системе отсчета равна нулю. Таким образом:

. (2.27)

Здесь — центробежный момент инерции для площадки S. Отметим, что для площадки симметричной относительно оси СХ центробежный момент инерции равен нулю.

Аналогичным образом находим проекцию :

и далее, с учетом формулы (2.26), получаем:

.

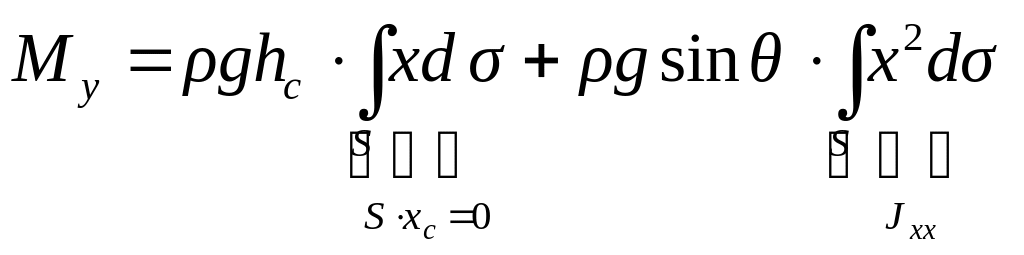Первое слагаемое в правой части последней формулы также равно нулю, поскольку координата центра тяжести в выбранной системе отсчета равна нулю. Величина представляет собой осевой момент инерции площадки . Очевидно, что этот момент инерции всегда положителен, так как положительна подынтегральная функция. Таким образом:

. (2.28)

Как уже было сказано, третья проекция вектора на ось CZ равна 0.

Найдем теперь в плоскости стенки такую точку D, что при перенесении в нее всех сил главный момент обращается в нуль. Очевидно, что эта точка не совпадает с центром тяжести, поскольку, как было показано, момент всех сил относительно центра тяжести отличен от нуля. Используя теорему о том, что при переходе к другому полюсу, главный вектор системы сил не изменяется, а главный момент изменяется на величину момента главного вектора относительно нового полюса, выбираем такую точку исходя из условий

здесь и — координаты искомой точки, которая называется точкой приложения равнодействующей системы сил давления или центром давления.

Используя полученные выше равенства (2.27), (2.28) и (2.19) получаем

, (2.29)

. (2.30)

Если обозначить расстояние от центра тяжести до линии пересечения плоскости стенки со свободной поверхностью (рис.2.14) через и заметить, что , то получим окончательно:

, . (2.31)

Можно сделать следующие выводы:

а) Система сил давления, действующих со стороны жидкости на плоскую стенку, сводится к одной равнодействующей, приложенной в специальной точке, центре давления;

б) Центр давления не совпадает с центром тяжести стенки, а лежит ниже его по отношению к свободной поверхности. Это следует из положительности осевого момента инерции. Если на свободной поверхности жидкости давление не равно атмосферному, а ниже его, то центр давления может находиться выше центра тяжести;

в) Для симметричной относительно оси СХ стенки центр давления лежит на оси симметрии.

Пример. Вычислить силу давления воды на наклонную стенку открытого сосуда, имеющую следующие размеры: ширина м, длина м, если угол наклона стенки к горизонту равен a = (рис. 2.15).

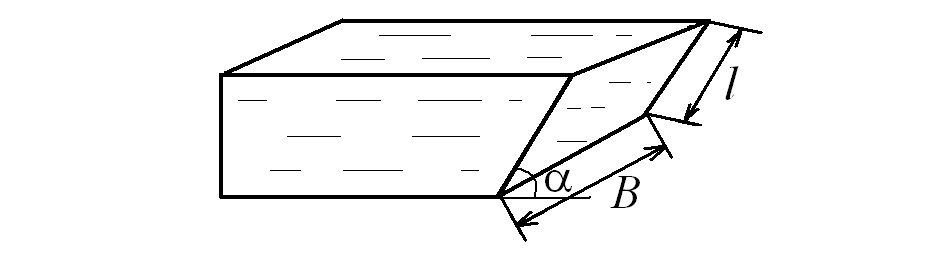
Рис. 2.15. Расчет силы давления на наклонную стенку

Решение. Глубина геометрического центра тяжести стенки под свободной поверхностью жидкости

,

следовательно, согласно формуле (2.23), имеем:

.

Ответ. Н ( кГс).

Пример. Расширяющийся к низу открытый резервуар отстойник (рис.2.16) имеет дно площадью 1 м², уровень осевшей воды равен h₁=0,3 м, уровень нефти h₂ = 1,3 м. Найти силу давления на дно резервуара, если плотности нефти и воды равны кг/м³, кг/м³, соответственно.

Решение. Силу давления на дно резервуара можно определить по формуле (2.24)

.

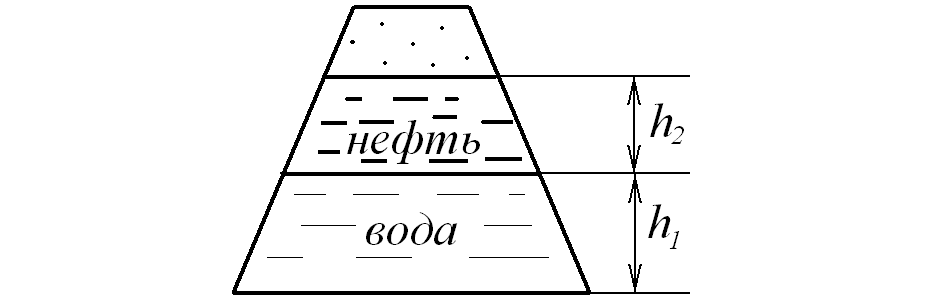
Рис. 2.16. Расчет силы давления на дно резервуара

Вычисляется избыточное давление в геометрическом центре тяжести поверхности дна:

Па

Вычисляется сила:

Н ( кГс).

Ответ. Н.