Теплоемкость жидкостей

Теплоемкостью вещества, в т.ч. жидкости, называют количество тепла, которое нужно передать единице массы этого вещества, чтобы увеличить его температуру на 1°С (Цельсия) или 1 К (Кельвина).

Из термодинамики известно, что эти количества различны в различных термодинамических процессах. Для веществ, уравнение состояния которых определяется давлением и удельным объемом , теплоемкости зависят от того, происходит ли передача тепла при постоянном давлении (т.е. в изобарическом процессе) или при постоянном объеме (т.е. в изохорическом процессе). В первом случае она обозначается , во втором - . В остальных термодинамических процессах теплоемкость С является линейной комбинацией теплоемкостей и .Как правило, . Для слабо сжимаемых капельных жидкостей .

Размерность теплоемкости следует из ее определения:

( обозначает размерность температуры). В системе СИ единицей измерения теплоемкости служит 1 :

.

Теплоемкость воды составляет 4200 , теплоемкость большинства нефтей лежит в пределах 1500-2500 или 350-600 .

Для того чтобы повысить температуру объема жидкости с плотностью от значения до значения , необходимо сообщить ей количество энергии , равное

. (2.10)

Здесь предполагается, что Однако в общем случае теплоемкость зависит от температуры и давления.

Теплопроводность жидкостей

Если разные части жидкости имеют различную температуру, то происходит перенос энергии от более нагретых слоев к более холодным. Если обозначить через вектор потока тепла, определяемый как количество тепловой энергии (Дж или кал), переносимое в единицу времени (с) через единицу площади (м²), то для него имеет место закон Фурье

, (2.11)

означающий, что вектор потока тепла пропорционален градиенту температуры. Известно, что вектор градиента

дает направление максимального увеличения температуры, а его проекция на направление в пространстве равна производной по этому направлению. Закон Фурье утверждает, что поток тепловой энергии в любом направлении пропорционален перепаду температур в этом направлении, а знак минус указывает, что тепло передается в направлении, противоположном градиенту температуры, т.е. от более нагретых слоев к более холодным.

Коэффициент , входящий в формулу (2.11), называют коэффициентом теплопроводности. Его размерность такова:

.

В системе СИ коэффициент теплопроводности выражается в :

.

Для воды этот коэффициент равен 0,6 при температуре 20°С, для нефтей он находится в пределах 0,1 - 0,2 . В общем случае коэффициент зависит от температуры, однако во многих случаях его можно считать постоянной величиной.

2.2. Уравнения равновесия жидкости (уравнения Эйлера)

Рассмотрим уравнения, определяющие распределение давления в покоящейся жидкости, т.е. жидкости, находящейся в равновесии под действием массовых сил в единице объёма среды . Эти уравнения получаются из общих уравнений движения жидкости, если в них положить:

• ;

• ;

• ,

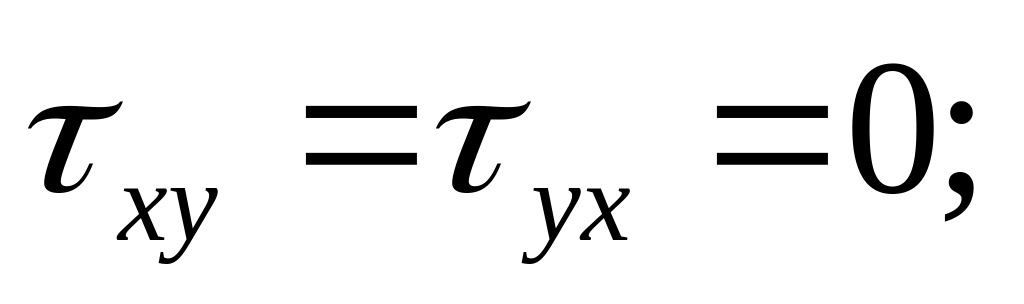
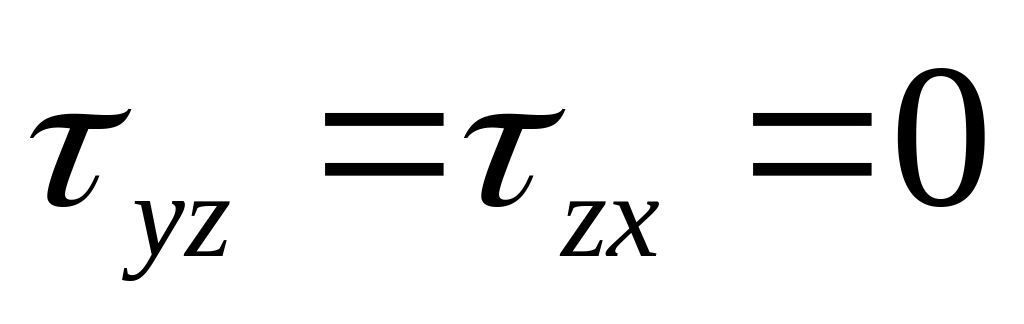тогда общие уравнения движения (1.30) приобретают вид:

или

(2.12)

Уравнения (2.12) называют уравнениями равновесия жидкости (уравнениями Эйлера). В векторном виде эти уравнения имеют вид:

. (2.13)

Смысл уравнений Эйлера ясен: градиент давления в жидкости уравновешиваются массовой силой в единице объёма среды , действующей в этом направлении. Отсюда следует, что производная от давления по координате в каждом направлении равна проекции массовой силы в единице объёма на это направление, уравнения (2.12).

Уравнения (2.12) можно привести к другому виду: первое уравнение умножить на dx, второе на dy, третье на dz и затем их сложить. Получим: .