21. Дослідження монотонності. Критичні точки.

Похідна функції має широке застосування при розв’язуванні різних задач математики, фізики, техніки та економіки. Так, наприклад, за допомогою похідної можна обчислити границю функції, знайти екстремум функції, інтервали монотонності, точки перегину функції та інше.

Інтервалами монотонності функції називаються ті інтервали, на яких функція або тільки зростає, або тільки спадає або залишається сталою.

Якщо неперервна на сегменті 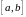функція має в кожній точці цього сегмента додатну похідну, то вона зростає на цьому сегменті, а якщо від’ємну похідну, то вона спадає на цьому сегменті.

Функція має максимум в точці 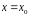, якщо для довільних точок із її околу виконується умова і має мінімум в точці, якщо виконується така умова: .

Максимум і мінімум функції називають екстремуми функції.

Необхідною умовою існування екстремуму в точці диференційовної функції є рівність нулю її похідної: .

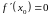К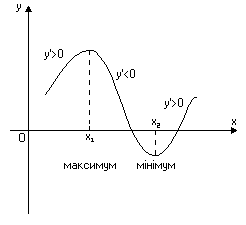 ритичними або стаціонарними точками неперервної функції є ті точки, в яких її похідна дорівнює нулю або не існує.

Д

Рис. 6

остатньою умовою існування екстремуму в точці для диференційовної функції є зміна знака похідної при переході через цю точку. Так при зміні знака з “+” на “–” в точці функція має максимум, а з “–” на “+” – мінімум (Рис. 6).

2

Рис. 7

2.Опуклим називається графік диференційовної функції в інтерва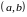лі , якщо він знаходиться нижче довільної його дотичної на цьому інтервалі.

Точкою перегину неперервної функції називається та точка, яка відділяє вгнутість від опуклості її графіка (Рис. 7).

Якщо друга похідна функції для всіх 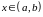від’ємна ( ), то тут графік функції опуклий, а якщо 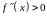– вгнутий.

Необхідною умовою існування точки перегину графіка функції є рівність нулю її другої похідної: 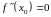в даній точці .

Точка , в якій , називається критичною точкою другого порядку для функції .

Достатньою умовою існування точки перегину графіка неперервної функції є зміна знаку другої похідної при переході через точку .

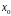Асимптотою графіка функції називається пряма лінія, до якої графік функції наближається на нескінченності.

Вертикальною асимптотою є прям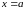а , якщо виконується умова .

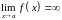Для функції вертикальні асимптоти існують в її точках розриву другого роду.

22.Опуклість графіку функції та точки перегину.

Опуклість і вгнутість кривих. Точка перегину

Нехай крива задана рівнянням , де - неперервна функція, що має неперервну похідну на деякому проміжку . Тоді в кожній точці такої кривої можна провести дотичну (ці криві ще називають гладкими кривими).

Візьмемо на кривій довільну точку , де , .

Означення. Якщо існує окіл точки такий, що для всіх відповідні точки кривої лежать над дотичною, проведеною до кривої в точці , то крива в точці називається вгнутою догори

Означення. Якщо існує окіл точки такий, що для всіх відповідні точки кривої лежать під дотичною, проведеною до кривої в точці , то крива в точці називається вгнутою донизу

Означення. Точка називається точкою перегину кривої, якщо існує окіл точки - такий, що для всіх крива вгнута по один бік, а для всіх - по другий бік (рис. 6.17, 6.18).

Якщо крива, задана рівнянням в кожній точці деякого проміжку вгнута догори, її називають вгнутою на цьому проміжку; якщо крива в кожній точці проміжку вгнута донизу, її називають опуклою на даному проміжку.

Не всяка крива має точку перегину. Так, криві, зображені на рис. 6.21, 6.22, точок перегину не мають. Іноді крива може мати тільки одну, а іноді кілька точок перегину, навіть нескінченну множину.

Для того, щоб знайти точки перегину кривої, заданої рівнянням , треба:

1) визначити від функції похідну другого порядку і прирівняти її до нуля . З коренів цього рівняння вибрати тільки дійсні корені і ті, які належать області існування функції;

2) в околі кожного вибраного таким чином кореня визначити знак похідної другого порядку спочатку при значеннях , менших від розглядуваного кореня, а потім при значеннях , більших за даний корінь. Якщо при переході через вибраний корінь похідна змінює знак, то точка є точкою перегину заданої кривої. Якщо при переході через знак похідної другого порядку не змінюється, то не є точкою перегину кривої.

Зокрема, якщо при переході через змінює знак "+" на "-", то крива при проходженні через точку перегину змінює відповідно свій вигляд із вгнутості на опуклість. Якщо при переході через змінює знак "-" на "+" , то крива при проходженні через точку перегину змінює відповідно свій вигляд з опуклості на вгнутість.