
- •3. Визначники 2-го, 3-го порядків
- •Властивості визначників 2-го, 3-го порядків
- •10. Множина.
- •11. Загальне поняття функції
- •Основні елементарні функції:
- •12. Числова послідовність. Границя числової послідовності.
- •13. Число е. Значення деяких границь числових послідовностей
- •15. Обчислення границь.
- •16. Неперервність.
- •18. Похідні від простих функцій
- •19. Правила обчислення похідних. Таблиця похідних.
- •Основні похідні
- •20. Теореми Ферма, Ролля, Лагранжа, Коші
- •21. Дослідження монотонності. Критичні точки.
- •22.Опуклість графіку функції та точки перегину.
- •23. Диференціал
- •24. Похідні старших порядків.
- •25. Первісна функції. Невизначений інтеграл.
- •26. Елементарні властивості невизначеного інтегралу. Таблиця основних інтегралів. Властивості невизначеного інтеграла
- •29. Розбиття відрізку. Інтегральна сума. Інтеграл Рімана.
Відповіді до екзамену з математики
1.Матрицею називається прямокутна таблиця (масив) з чисел, що містить m рядків та n стовчиків. Числа m та n називають порядком матриці. Якщо m=n, то матрицю називають квадратною.
![]() або
або
![]() ,
де aij — елементи матриці, причому індекс
і в елементі означає номер рядка, a j—
номер стовпця, на перетині яких стоїть
даний елемент.
,
де aij — елементи матриці, причому індекс
і в елементі означає номер рядка, a j—
номер стовпця, на перетині яких стоїть
даний елемент.
Основні дії над матрицями:
1.Операція додавання матриць вводиться тільки для матриць однакового розміру. Сумою С = А + В двох матриць Аm×n — (aij) і Вm×n = (bij) називається матриця Сm×n= (cij)=(aij+bij). Наприклад,
![]()
2. Добутком матриці Аm×n = (aij) на число k (або числа k на матрицю Am×n) називається матриця Вm×n= (kaij). Наприклад,
![]()
Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В. Якщо ця умова не виконується, тобто матриці неузгоджені, то множення таких матриць неможливе.
Добутком С = А В матриці Аm×n — (аij) на матрицю Bn×k=(bij) називається така матриця, у якої елемент сij дорівнює сумі добутків елементів j-го рядка матриці А на відповідні елементи четвертого стовпця матриці В:
cij=ai1b1j+ai2b2j+ … + ainbnj; C = Cm×k = (cij),
i = 1, 2, …, m; j = 1, 2, …, k.
Це означення називають правилом множення рядка на стовпець. Наприклад, щоб визначити елемент с24, що стоїть в другому рядку і четвертому стовпці матриці С = АВ, потрібно знайти суму»добутків елементів другого рядка матриці А на відповідні елементи четвертого стовпця матриці В.
Обернена матриця. Нехай А — квадратна матриця. Матриця A-1 називається оберненою до матриці А, якщо виконується умова
А А-1 = А-1А = Е.
![]()
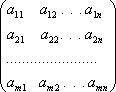
2. Визначник – це число. Розглянемо довільну матрицю n-го порядку
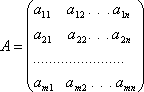 .
З кожною такою матрицею зв’язано цілком
визначену чисельну характеристику, яку
називають визначником, що відповідає
цій матриці.
.
З кожною такою матрицею зв’язано цілком
визначену чисельну характеристику, яку
називають визначником, що відповідає
цій матриці.
З точністю до знака, визначник матриці виражає коефіціент, на який множаться -мірні об'єми під дією цієї матриці.
Мінором
Mij
елемента аij визначника називається
визначник, який утворюється з даного
визначника в результаті ви креслення
і-рядка та j-стовчика, тобто рядка і
стовчика на перетині яких стоїть аij.
Мінор
![]() квадратної
матриці А — визначник матриці, отриманий
шляхом викреслювання рядка 2 та стовпчика
3:
квадратної
матриці А — визначник матриці, отриманий
шляхом викреслювання рядка 2 та стовпчика
3:
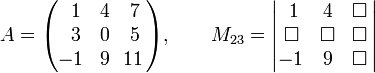
![]()
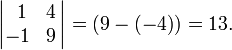
Алгебраїчним
доповненням Аij елементом аij називається
мінор взятий зі знаком
![]() тобто
тобто
![]()
3. Визначники 2-го, 3-го порядків
Def. Значення
виразу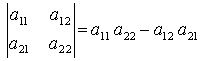 (1.1)
(1.1)
називають визначником (детермінантом) другого порядку.
Def. Значення виразу
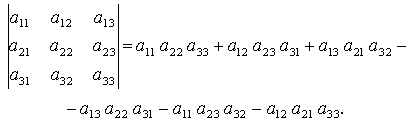 (1.2)
(1.2)
називають визначником третього порядку.
Порядок визначника дорівнює числу його рядків (число стовпців співпадає з числом рядків).
Символи ![]() називають
елементами визначника, причому перший
індекс
називають
елементами визначника, причому перший
індекс ![]() вказує
номер рядка, а другий індекс
вказує
номер рядка, а другий індекс ![]() –
номер стовпця, на перетині яких стоїть
даний елемент.
–
номер стовпця, на перетині яких стоїть
даний елемент.
Якщо всі елементи є числами, то зрозуміло, що результатом обчислення визначника також є число.
Елементи ![]() ,
, ![]() у
визначнику другого порядку і
,
у
визначнику другого порядку і
, ![]() ,
, ![]() у
визначнику третього порядку
складають головну
діагональвизначника,
а елементи
у
визначнику третього порядку
складають головну
діагональвизначника,
а елементи ![]() ,
, ![]() та
та ![]() ,
,
,
, ![]() – побічну
діагональ.
– побічну
діагональ.
Для обчислення визначника другого порядку необхідно від добутку елементів головної діагоналі відняти добуток елементів побічної діагоналі.
Визначник третього порядку можна обчислити за правилом трикутника. Перші три доданки, які беруть зі знаком плюс, є добутками елементів, що стоять на головній діагоналі і в вершинах двох трикутників, у яких одна сторона паралельна головній діагоналі.
Наступні три доданки, які беруть зі знаком мінус, є добутками елементів, що стоять на побічній діагоналі та у вершинах двох трикутників, у яких одна сторона паралельна побічній діагоналі.
Для запам’ятовування цієї формули зручно користуватися схемою, зображеною на рис. 1.
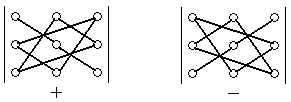
Рис 1. Схема обчислення за правилом трикутника
N.B.При обчисленні визначників використовують формулу
 .
.
Властивості визначників 2-го, 3-го порядків
Сформулюємо найважливіші властивості визначників на прикладі визначників третього порядку. Правильність цих властивостей можна встановити, наприклад, безпосередньою перевіркою. Всі властивості виконуються також для визначників довільного порядку.
1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями:
 .
.
Ця властивість указує на рівноправність рядків і стовпців визначника.
2. Визначник змінить знак на протилежний, якщо переставити місцями два рядки (два стовпці). Наприклад,
 .
.
3. Якщо всі елементи рядка (стовпця) дорівнюють нулю, то визначник дорівнює нулю.
4. Визначник з двома однаковими рядками (стовпцями) дорівнює нулю.
5. Спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника. Наприклад,
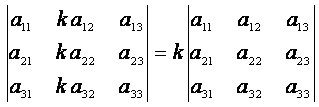 .
.
6. Визначник, який містить два пропорційні рядки (стовпці), дорівнює нулю. Наприклад,
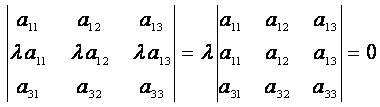 .
.
7. Якщо елементи деякого рядка (стовпця) є сумою двох доданків, то визначник дорівнює сумі двох визначників. Наприклад,
 .
.
8. Якщо до елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число, то значення визначника не зміниться. Наприклад,
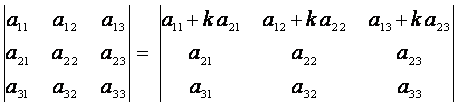 .
.
4. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:
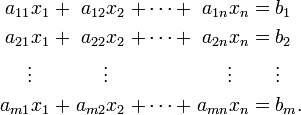
Це система m лінійних рівнянь з n невідомими, де
![]() є
невідомими,
є
невідомими,
![]() є
коефіцієнтами системи,
є
коефіцієнтами системи,
![]() -
вільними членами[1].
-
вільними членами[1].
Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.
№ 5.У загальному випадку система m лінійних рівнянь з n невідомими x1x2xn
має слідуючий вигляд:
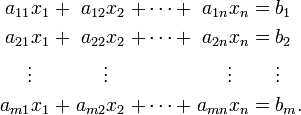
Метод Крамера (Крамера правило) — спосіб розв'язання квадратних систем лінійних алгебраїчних рівнянь із ненульовим визначником основної матриці (при цьому для таких рівнянь розв'язок існує і є єдиним).
Теорема (правило Крамера). Якщо визначник системи лінійних алгебраїчних рівнянь з невідомими відмінний від нуля, то система має розв'язок і при тому єдиний, який знаходиться за формулами.
Матричний метод розв’язання систем лінійних алгебраїчних рівнянь
Суть методу
Якщо
A — основна матриця системи,
b— вектор-стовпчик вільних членів,
x— вектор-стовпчик невідомих;
то має місце рівність:
Ax=b,
Якщо матриця A є квадратною та невиродженою, то для неї існує обернена матриця. Помноживши обидві частини рівняння зліва на A-1, отримаємо A-1Ax=A-1b
Оскільки A-1=I та Ix=x , то отримаємо формулу: x= A-1b
№6
Ранг матриці — порядок найбільших відмінних від нуля мінорів цієї матриці (такі мінори називаються базисними).
Ранг системи векторів — найбільше число лінійно-незалежних векторів з цієї системи.
Зазвичай ранг матриці А позначається rang A(rg A) чи rank A.
Теорема Кронекера-Капеллі: Система лінійних рівнянь має розв'язок тоді і тільки тоді, коли ранг матриці, складеної з коефіцієнтів при невідомих, не змінюється при додаванні до неї стовпця вільних членів (розширена матриця). Цей розв'язок єдиний, якщо цей ранг матриці дорівнює кількості невідомих.
7. Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь.
Початок
алгоритму. 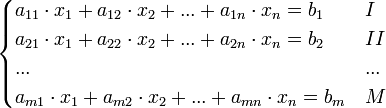
Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться доверхньотрикутного вигляду.
З цього моменту починається зворотний хід.
З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок.
8. Пряма належить площині, якщо дві довільні точки прямої належать цій площині.
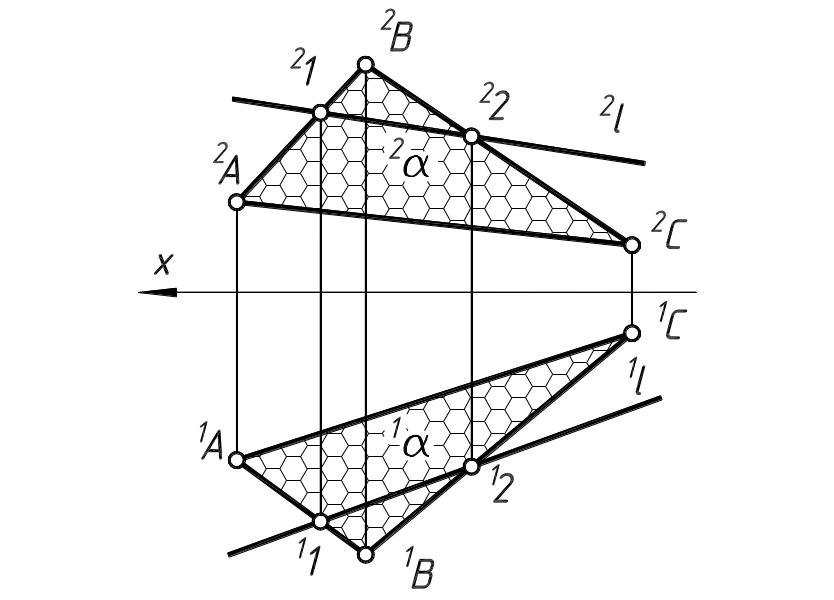
Рис. 3.8
Пряма
l
належить площині (ΔАВС),
тому що вона проходить через точки 1, 2,
що належать цій площині:
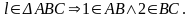
Серед прямих, які належать площині, виділимо два класи прямих, які відіграють роль при розв’язуванні задач – це горизонталі і фронталі площини.
Горизонталь – це лінія, що належить площині і паралельна горизонтальній площині проекцій (рис.3.9).
Фронталь площини - f називається пряма, яка належить площині і паралельна фронтальній площині проекцій (рис. 3.10)
9. Теорема 1. Кожна площина в прямокутній декартовій системі координат визначається рівнянням першого степеня і навпаки, кожне рівняння першого степеня в просторі визначає деяку площину.
Доведення.
Нехай, задано площину ![]() в
прямокутній системі координат. Як
відомо, три точки цілком визначають
площину. Візьмемо три точки
в
прямокутній системі координат. Як
відомо, три точки цілком визначають
площину. Візьмемо три точки ![]()
![]()
![]() з
площини
.
Нехай тепер
з
площини
.
Нехай тепер ![]() -
довільна точка цієї площини.
-
довільна точка цієї площини.
Розглянемо
вектори ![]() .
Ці вектори лежать в площині
,
тобто є компланарними. За умовою
компланарності трьох векторів
.
Ці вектори лежать в площині
,
тобто є компланарними. За умовою
компланарності трьох векторів ![]() .
Позначимо
.
Позначимо ![]() вектор
перпендикулярний до площини
.
Тоді, враховуючи, що
вектор
перпендикулярний до площини
.
Тоді, враховуючи, що
![]()
умову
можна
записати у вигляді ![]() .
.
Останнє
рівняння задовільняють тільки координати
точок, які лежать в площині
, тобто
це рівняння визначає площину
.
Його можна записати у вигляді ![]() , де
, де ![]() .
.
Цим доведена перша частина теореми, бо одержане рівняння є рівнянням першого степеня, або лінійним рівнянням. Другої частини теореми доводити не будемо.
Наслідок.
Рівняння площини, яка проходить через
три точки ![]() має
вигляд
має
вигляд 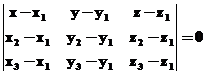 .
.
Отже,
згідно теореми кожне рівняння
виду
визначає
деяку площину в прямокутній системі
координат, причому вектор ![]() є
перпендикулярним до цієї площини.
є
перпендикулярним до цієї площини.
Рівняння називають загальним рівнянням площини.
Розглянемо деякі частинні випадки загального рівняння.
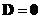 .
Координати початку координат
.
Координати початку координат 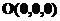 задовільняють
рівняння
задовільняють
рівняння 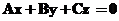 .
Це значить, що площина проходить через
початок координат.
.
Це значить, що площина проходить через
початок координат.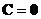 .
Вектор
.
Вектор 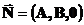 перпендикулярний
до осі
перпендикулярний
до осі  .
Це означає, що площина
.
Це означає, що площина 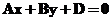 проходить
паралельно осі
.
проходить
паралельно осі
.
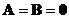 .
Вектор
.
Вектор 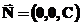 перпендикулярний
до осей
перпендикулярний
до осей 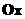 та
та 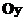 ,
тобто до площини
,
тобто до площини 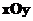 .
Отже, площина
.
Отже, площина 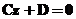 проходить
паралельно координатній площині
проходить
паралельно координатній площині 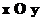 .
.
Висновки з п.2,3 можна також робити нагадавши рівняння циліндричної поверхні.
Якщо
площина не проходить через початок
координат і перетинає всі координатні
осі, то її рівняння можна записати у
вигляді ![]() -
-
рівняння площини у відрізках на осях.
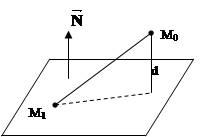 Теорема
2.
Віддаль від точки
Теорема
2.
Віддаль від точки ![]() до
площини
до
площини
визначається
за формулою 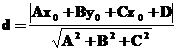 .
.
Дійсно, ![]() ,
де
,
де
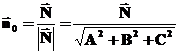 -
орт вектора
-
орт вектора ![]()
![]() .
.
За властивістю 2 скалярного добутку
![]()
![]()
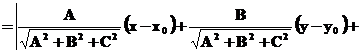
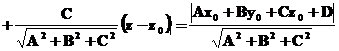 .
.
Число ![]()
![]() називається
відхиленням точки
називається
відхиленням точки
від
площини
. ![]() ,
якщо початок координат і точка
,
якщо початок координат і точка ![]() лежать
по різні сторони від площини та
лежать
по різні сторони від площини та ![]() ,
якщо початок координат і точка
лежать
по одну сторону від площини.
Знак
,
якщо початок координат і точка
лежать
по одну сторону від площини.
Знак ![]() або – залежить
від знаку при
або – залежить
від знаку при
![]() . У
відхилення беруть знак протилежний
знаку
.
. У
відхилення беруть знак протилежний
знаку
.
Теорема
3.
Кут між двома площинами ![]() та
та ![]() можна
знайти з формули
можна
знайти з формули
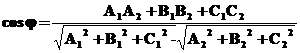 .
.
Дійсно,
кут між даними площинами чисельно рівний
куту між перпендикулярними до них
векторами ![]() та
та ![]() .
.
Цей кут знаходиться за вказаною формулою.
Наслідок
1.
Умовою перпендикулярності вказаних в
теоремі площин є умова ![]() .
.
Наслідок
2.
Умовою паралельності вказаних площин
є умова ![]() ,
тобто умова колінеарності векторів
,
тобто умова колінеарності векторів ![]() та
та ![]() ї
ї
