19. Правила обчислення похідних. Таблиця похідних.

Отже, якщо не зважати на механічний та геометричний зміст попередніх задач, а виділити спільних метод їх розв'язку приходимо до поняття похідної. Похідною функції   у точці   називається границя (якщо ця границя існує) відношення приросту функції до приросту аргументу, що прямує до нуля так що:

.

За допомогою похідної також можна визначити силу струму, як границю  , де   — додатній електричний заряд, який проходить через провідник за час  , а також багато інших задач фізики та хімії.

Похідну функції   позначають  .

Якщо функція   має похідну у точці  , то вона визначена як у самій точці  , так і у деякому околі цієї точки та неперервна у точці  . Проте, обернене твердження змісту не має. Наприклад, неперервна у кожній точці функція  , графіком якої є бісектриси першого та другого координатних кутів, при   не має похідної, оскільки відношення   не має границі при  : якщо  це відношення дорівнює  , а якщо  , то воно дорівнює  . Більш того, існують неперервні функції, які не мають похідної в усіх точках.

Операцію знаходження похідної називають диференціюванням. На класі функцій, що мають похідну, ця операція лінійна.

Якщо функція є складеною, тобто   та  , або всерівно що  , то 

Якщо похідна   має похідну, то її називають другою похідною функції   та позначають  . З механічної точки зору друга похідна — це прискорення.

Аналогічним чином дається визначення похідної вищого порядку. Похідна порядку n позначається:  .

Таблиця похідних

Основні похідні

• Похідна від сталої: 

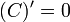
• Похідна від степеневої функції: 

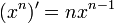
• Похідна від показникової функції: 

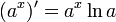
• Похідна від експоненти: 

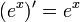
• Похідна від логарифмічної функції: 

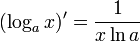
• Похідна від натурального логарифму: 

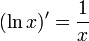
• Похідна від синуса: 

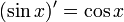
• Похідна від косинуса: 

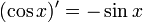
20. Теореми Ферма, Ролля, Лагранжа, Коші

Велика теорема Ферма (відома теорема Ферма, остання теорема Ферма) — твердження, що для довільного натурального числа рівняння (рівняння Ферма) не має розв´язків у цілих числах відмінних від нуля.

Вона була сформульована приблизно в 1637-му році французьким математиком П'єром Ферма на полях книги Діофанта "Арифметика"

Теоре́ма Ро́лля — теорема, що стверджує, що між двома рівними значеннями диференційовної функції обов'язково лежить нуль похідної цієї функції.

Формулювання. Нехай функція неперервна на проміжку , диференційована в усіх внутрішніх точках проміжку . Нехай, окрім того, . Тоді на проміжку знайдеться принаймні одна точка така, що значення похідної у цій точці дорівнює нулю.

Теорема має простий геометричний зміст: якщо кінцеві ординати кривої рівні, то, згідно з теоремою Ролля, на цій кривій знайдеться точка, у якій дотична до кривої паралельна до осі .

Теоре́ма (формула) Лагра́нжа про скінче́нні при́рости. Доведена французським математиком і механіком Жозефом Луї Лагранжем.

Формулювання теореми. Якщо функція неперервна на проміжку , диференційована в , то знайдеться принаймні одна точка така, що має місце формула:

.

Ця формула і називається формулою Лагранжа, або формулою про скінченні прирости.

Теорема Коші, що належить французькому математикові Огюстену Коші й називається узагальненою теоремою про скінченні прирости. Вона узагальнує теорему Лагранжа.

Формулювання теореми. Якщо кожна з двох функцій та неперервна на проміжку та диференційовна в усіх внутрішніх точках цього проміжка і якщо, окрім того, похідна відмінна від нуля скрізь у проміжку , то на цьому проміжку знайдеться точка така, що має місце формула:

Формулу (1) називають узагальненою формулою скінченних приростів, або формулою Коші.