35.Признаки сравнения для исследования сходимости числовых рядов с положительными членами.
Признаки:
1)признак сравнения.
Пусть даны два ряда с полож. член. Σ n=1 Un (1) и Σ n=1 Vn (2), причем члены первого ряда не превосходят членов второго , т.е. при n є R ; Un =< Vn
Тогда 1)если сходится ряд (2) ,то сходится и (1)… 2) если расходятся ряд(1), то расходится и ряд (2).
«Эталонные ряды»:1. геометрический ряд сходятся при |q| <1 и расходится при |q|>=1.
2. гармонический ряд расходятся.
3. обобщённый гармонический ряд Σ n=1 1/nα = 1+1/2α+ 1/3α+…+1/nα +…
Сходится при α>1 и расходится при α=<1.
2) Предельный признак сравнения
Если Σ n=1 Un и Σ n=1 Vn – ряды с полож. член. И существует конечный предел отношения их общих членов Limn-> Un\Vn = R≠0, то ряды одновременно либо сходятся ,либо расходятся.
3)Признак Даламбера.
,тогда если L<1,ряд сходится; L>0,ряд расходится; L=0-применить другой признак.
4)признак коши.
Если L>1-расходится L<1-сходится L=1-неизвестно.
> Особенности :
1. если Limn-> Un+1/Un = или Limn-> n√Un = , то ряд расходится.
2. если Limn-> Un+1/Un =L=1 или Limn-> n√Un =1, то неизвестно.
5)Интегральный признак сходимости .
Пусть члены ряда не возрастают, т.е. существует функция f(x)-определение при х - непрерывная и возрастающая, тогда для сходимости ряда необходимо и достаточно, чтобы несоответ. -сходится.
36.Понятие ф-ции нескольких переменных, предел и непрерывность ф-ции.
Опред-е: Пусть имеется 3 числовых мн-ва X,Y,Zпринадлежащих R.
Действительной ф-цией 2ух переменных x,y наз-ся отображ-е f:X∙Y→Z, Z=f(x,y), кот устанавливает соответствие между парой <x,y>принадл X∙Y, х(принадл)Х, y(принадл)Y и числом z(принадл)Z. Каждому Z соотв-ет одна пара x,y.
Геом интерпр: График-мн-во точек в трёхмерн простран-ве X,Y,Z, это некотор поверх-ть.
Предел и непрерывность.
Число А-предел ф-ции Z=f(x,y) в т.М0(х0,у0), если для любого сколь угодно малого положит числа >0, найдётся положит число ∂>0(зависящее от Е, ∂=∂(Е)), такое что для всех точек М (x,y), отстоящих от т.М0(х0,у0) на расст ρ меньше, чем ∂ (0<ρ<∂) выполняется |f(x,y)-A|<E или lim(x→x0, y→y0)f(x,y)=A.
Ф-ция Z=f(x,y) непрерывна, если выполняется три усл:
1)она определена в этой т.(x0, y0)
2)сущ-ет конечный предел функции в т.М0.
3)этот предел=значению ф-ции lim(x→x0, y→y0)f(x,y)=f(x0, y0) в т.(x0, y0)
37.Частные производные ф-ции 1го порядка и полный дифференциал.
∆z-полное приращение ф-ции в т.(x,y)
∆z=f(x+∆x, y+∆y)-f(x,y)
Частная производная ф-ции неск перемен-х по одной из этих переменных - предел отношения соответствующего частного приращения ф-ции к приращению рассматриваемой независимой переменной при стремлении последующего к нулю(если предел сущ-ет).
Обозначается Z’x, Z’y или ∂z\∂x, ∂z\∂y или fx’(x,y), fy’(x,y)/
Z’x=lim(∆x→0)∆xZ\∆x=lim(∆x→0)f(x+∆x,y)-f(x,y)\ ∆x
Z’y=lim(∆y→0)∆yZ\∆y=lim(∆y→0)f(x,y+∆y)-f(x,y)\ ∆y
Дифференциалом ф-ции наз-ся сумма произведений частных производных этой ф-ции на независимых переменных.
Dz= z’x∆x +z’y∆y или dz=(∂z\∂x)dx+(∂z\∂y)dy
Ф-ция z=f(x,y) диффеоенцируема в т.(x,y), если её полное приращение можно представить в виде ∆Z=dz+α∆x+β∆y, где dz-дифференциал ф-ции, αβ-бескон.малые при (∆x→0,∆y→0)
Необходим усл:сущ-ние частн произодных.
Достатачное: если частная производная ф-ции сущ.в т. М(х,у) и непрерывна в этой окрестности, то функция z=f(x,y) дифференцируема в этой точке, т.е. ее полное приращение может быть представлено как сумма дифференциала этой функции:
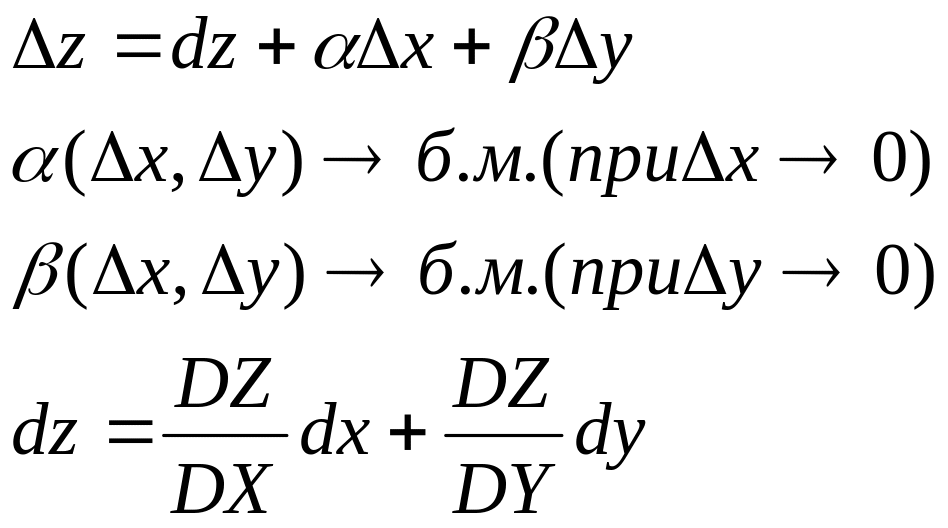
38.Производная по направлению, градиент.
Производной Z’ℓ по напр ℓ ф-ции двух перемен-ых z=f(x,y) наз-ся предел отношения приращения ∆ℓ при стремлении последней к 0, т.е Z’ℓ= lim(∆ℓ→0)∆ℓZ\∆ℓ
∆ℓZ=f(x+∆x,y+∆y)-f(x,y)=f(x+∆x,y+∆y)-f(x,y+∆y)+ f(x,y+∆y)-f(x,y)
Z’ℓ =lim(∆ℓ→0)∆xZ(x,y+∆y)\ ∆ℓ+ lim(∆ℓ→0)∆yZ(x,y)\ ∆ℓ
Градиент.▼Z – вектор, у кот координаты явл-ся частными производными: ▼Z(Z’x,Z’y)
Произв-я по напр есть скалярн произвед-е Гр.▼Z и единичного вектора, задающего направление ℓ.
(▼Z,e)= Z’x cosα+ Z’y cosβ
Градиент ф-ции в дан точке хар-ет направ-е максимал-ой скорости изменения ф-ции в этой точке.
Тоерема: Пусть задана диф-мая ф-ция z=f(x,y) и пусть в т. М(х0,у0) величина градиента отлична от 0. Тогда градиент функции в т. М(х0,у0) перпендикулярен линии уровня, проходящей через дан точку.
39.Экстремумы ф-ции многих переменных, необходимое и достаточное условия экстр-ма.
Т. М(х0,у0) – т-ка максимума(минимума)ф-ции z=f(x,y), если сущ-ет окрестность т.М такая, что для всех точек (х,у) из этой окрестности выполняется неравенство:
f(x0,y0)≥f(x,y); f(x0,y0)≤f(x,y).
Теорема. Пусть т.(x0,y0) есть точка экстремума диф-ой ф-ции z=f(x,y). Тогда частные произ-ые fx’(x0,y0) и fy’(x0,y0) в этой точке равны 0.
Необходимое условие экстремума:
В т. Минимума или макс-ма диф-ой ф-ции градиент равен 0. В т. экстремума обращаются в 0 произв-ие ф-ции по всем направлениям.
Необходи усл: (аналог теории Ферма). Если в т. М0(х0,у0) ф-ция имеет экстремум, то в этой т. частн производные равны 0.
Достаточн усл: z=f(x,y) определена в окрестности критической т.М(х0,у0), в кот fx’(x0,y0)=0, fy’(x0,y0)=0 и имеет в этой т. непрерыв вторые частн производные: f”xx=A, f”xy=f”yx=B, f”yy=C. тогда если ∆=AC-B2>0, то в т. М экстремум сущ-ет, причем если A>0, то min, A<0, то max. Если ∆<0, то экстремума нет, если ∆=0, то неопределённость.
40.Условный экстремум. Нахождение методом множителей Лагранжа.
Задана ф-ция z=f(x,y) и ур связи g(x,y)=0
Т. М(x0,y0) –т.условного экстр, если сущ-ет такая окрест этой точки, что для любых т.N этой окрест, находящихся на этой линии, удовлетворяющих ур-ю g(x,y)=0, выполняется неравенство: f(x0,y0)≥f(x,y)-max; f(x0,y0)≤f(x,y)-min.
Метод Лагранжа. Если т.М(x0,y0) яв-ся точкой усл.экстр-а ф-ции z=f(x,y) при усл g(x,y)=с, то сущ-ет значение λ0 такое, что т.(x0,y0,λ0) яв-ся точкой экстр-ма ф-ции L(x,y, λ). Система:
∂L\∂x=f’x(x,y)+ λg’x(x,y)=0
∂L\∂y=f’y(x,y)+ λg’y(x,y)=0
∂L\∂λ=gx(x,y)=0
х,у – критич точки.
41. Кратные интегралы. Сведение кратного интеграла к повторному.
Пусть передл I интергрируемой суммы S для ф-ции z=f(x,y) по области D при стремлении подобласти d к 0 существует, конечен и не зависит от способа разбиения обл D на элементарные части и выбора точек (ξi,γi) в обл Di. Тогда ф-уия Z наз-ся интегрируемой в обл D, а число I – двойным интегралом от дан ф-ции по обл D и обозначается I=∫∫Df(x,y)dxdy.
Достат.усл интегрируемости. Если ф.Z непрерывна в обл D, то она интегрируема в этой обл.
Геом смысл.Двойн.инт = объему цилиндрич.тела, построенного на обл D как на основании и огранич-го сверху пов-тью z=f(x,y).
Сведение к повторному:
∫∫Df(x,y)dxdy=∫badx∫φ(x)x(x)f(x,y)dy