1.Понятие действительной функции действительной переменной. Способы задания функции. График. Сложная и взаимообратные функции.

Если каждому значению х(х и Х) ставится в соответствие попределЁнное значение у(у и У), то говорят что на множестве х задана функция у=f(x). Где у-зависимая переменная. F-з-он соответствия. x-независ переменная(аргумент). Функция является правилом. Множество-совокупность объектов, относительно которых можно сказать, принадлежат ли они данной совокупности или нет.

Способы задания функции:

1.Аналитический(с помощью формулы).

2.Табличный-ф.задана таблицей, содержащей значение аргумента(х) и соответ. значение ф-ии f(x).

3.Графический-задана графиком.

4.Словесный.

5.С помощью комп.программы.

График функции- множество точек (x,y) плоскости, абсциссы которых есть значения аргумента х, а ординаты- соответствующие им значения функции y=f(x).

Сложная функция. Пусть ф. y=f(U)-ф-я от переменной U, определЁнной на множестве U c областью значения Y, а переменная U в свою очередь является ф-ей U=f(x) от переменной х, определЁнной на множстве Х с областью значений U.=> сложной функцией называют ф. вида y=f[ℓ(x)], заданную на множестве X. Пример: y=lgsinx. y’x=y’uU’x.

2.Основные свойства функций. Примеры функций, используемых в экономике.

Свойства функций:

1. Чётность-если f(-x)=f(x). (f(-x)=(-x)²=x²=f(x)).Симметрично относительно оси ординат. 2. НечЁтность-если f(-x)=-f(x). Симметрично относительно начала координат. Также функция может быть ф-ей общего вида.

Монотонность: ф-я y=f(x)-возрастающая(убывающая) на промежутке х, если большему значению аргумента из этого промежутка соответствует большее(меньшее)значение ф-ии. Х₂>X₁, y=f(x).

Строго монотонные:f(X₂)>f(X₁)-возраст. f(X₂)<f(X₁)-убыв. Монотонные: f(X₂)≥f(X₁)-неубывающ. f(X₂)≤f(X₁)-невозраст.

Периодичность: ф-я y=f(x)-периодическая с периодом Т≠0, если для любых х из области определения ф-ии f(x+T)=f(x). Пример:sin(x)=sin(x+2П). sin2x=sin(x+T)=sin(2x+2T)=>2T=2П. Т=П..

Ограниченность: у=f(x)-ограниченная на промежутке x если существует такое положительное число М, что │f(x)│=М для любого х € Х. В противном случае-неогран.

Функции в экономике: 1.Ф-я полезности-зависимость полезности(результата), эффекта некоторого действия от рез-та этого действия.

2.Производственная ф.-завис. рез-та деят-ти от обусловивших еЁ факторов.

3.Ф-я выпуска-завис-ть объЁма про-ва от потребления ресурсов.

4.Ф-я издержек-завис-ть издержек от объЁма выпуска продукции.

5.Ф-я спроса, потребления, предложения-зав-ть объЁма спроса, потребления, предлож на отдельные товары, услуги, от различных факторов(доход и т.п. и т.д.). Пример-график пересечения спроса и предложения, где на пересечении-«равновесная цена».

3.Понятие числовой последовательности и основные св-ва сходящихся последовательностей.

Определение: Если по некоторому з-ну каждому натуральному числу n поставлено в соответствие вполне определЁнное число a_n , то говорят, что задана числовая последовательность {a_n}. Числовая послежовательность-это функция натурального аргумента а_n=f(n). чатсный случай действительной переменной, когда аргументом является натуральное число. {a_n}=2, 1 1/2, 1 1/3,…1 1/100…a_n=1+1/n.

Св-во сходящихся последовательностей, имеющих предел:1.Если Xn=a, то limXn=a(n->∞)

2.Сходящаяся последовательность ограничена, однако не любая ограниченная последовательность сходится. limXn=(n->∞)a, limYn=b(n->∞).

3.lim(Xn±Yn)=a±b(n->∞).

4.lim(Xn*Yn)=ab(n->∞).

5.lim(Xn/Yn)=a/b(b+0).

6.Критерий коши:limXn=a(n->∞), limYn=a, {Zn}. Xn≤Zn≤Yn=>limZn=a(n->∞).

4.Предел числовой последовательности. Признаки существования предела последовательности. Два замечательных предела. Число А-предел числовой последовательности Х{an}, если для любого, даже сколь угодно малого положительного числа E>0, найдЁтся такой номер N(зависимый от Е, N=N(E)), что для всех членов последовательности с номерами n>N верно неравенство |an-A|<E. Обозначается liman(n->∞)=A или an>A при an(n->∞). Последовательность, имеющая предел-сходится, не имеющая-расходится.

Признаки существования предела:1.если числовая послеlовательность {a_n} монотонна и ограничена, то она имеет предел. 2.Если в некоторой окрестности точки Х0(или достаточно близких значениях Х) функция f(x) заключена между двумя функциями g(x) и ℓ(х) имеется одинаковый предел A при x->x₀(или x->∞), то функция f(x) имеет тот же предел А. Пусть при x->x₀ limy(x)=A, limℓ(x)=A(x->x₀) это означает, что для любого E>0 существует такое «знак существования»∂(E) ∂>0, что для всех х≠x₀ удовлетворяющее условию |x-x₀|< ∂верны неравенства

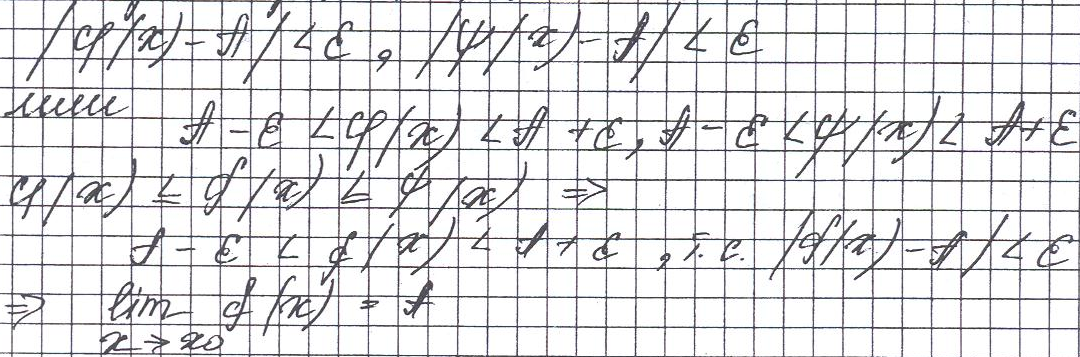
Замечательный предел. Предел sinx/x при х->0. LIMsinx/x=1. Док-во:

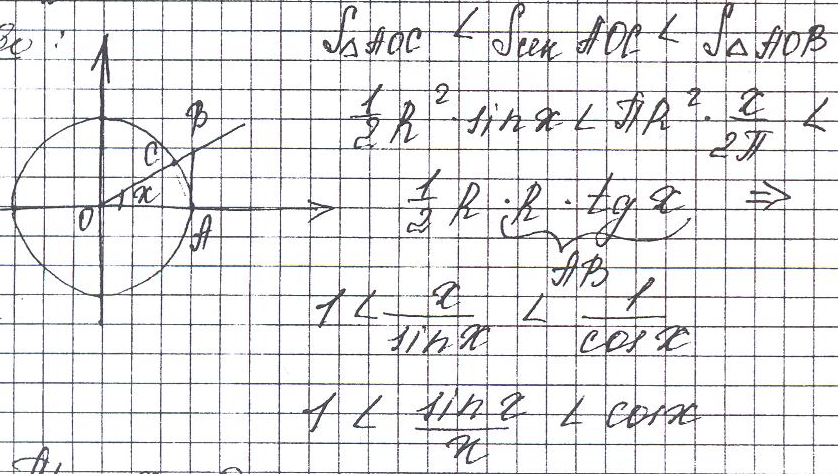
При х->0: cos x->1=>lim sinx/x=1(x->0) по второму признаку. Lim(1+1/n)ⁿ=e(n->∞)

(число эйлера 2.718).

Lim(1+1/x)^x=e(n->∞). 1/x=h(x), при x->∞, h(x)-б.м. lim(1+h)^1/h=e (1^∞)

5.Предел функции в бесконечности и в точке. 1.В бесконечности. n-ненатуральное, а действительное число. Число А-предел функции y=f(x), при x->∞, если для любого сколь угодно малого положительного числа E>0, найдЁтся такое положительное число S>0 (зависящее от E; S=S(E)), что для всех х, таких, что |x|>S верно

|f(x)-A|<E Limf(x)=A(x->∞) или f(x)->A при x->∞.

2.В точке. Число А-предел функции y=f(x) при x->x₀ если для любого, сколь угодно малого E>0 найдЁтся такое б>0, зависящее от Е, то для всех х≠х₀ и одновременно х->х₀<б будет выполняться |f(x)-A|< E

Любой E>0 принадлеж. б(Е)>0 любых х х≠0. |x-x₀|<б(Е)=>|f(x)-A|<Elimf(x)=Ax->x₀

F(x)->A

{x*|x-x₀|<б}-б-окрестность.

6.Непрерывность функции действительной переменной в точке и на отрезке. Св-ва функций, непрерывных на отрезке. Определение:функция f(x) называется непрерывной в точке х_0, если она удовлетворяет трЁм условиям: 1.Определена в точке х₀(сущ f(x₀)) 2.Имеет конечный предел функции при х->x₀. 3. Этот предел равен значению функции в точке x₀ т.е. limf(x)=f(x₀)(х-> x₀). Функция f(x)=y-непрерывная на промежутке х, если она непрерывна в каждой точке этого промежутка. Все элементы ф-ии непрерывны вьобласти их определения. Функ. y=f(x)-непрерывна в т. x₀ , если она определена в этой точке, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Св-ва ф-ии непрерывных на отрезке. 1.Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке(првая теорема вейерштрасса).

2. если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения т.м, наибольшего значения М(вторая теорема вейерштрасса)

3.Если функция y=f(x) непрерывна на отрезке [a,b] и значения еЁ на концах отрезка f(a) и f(b) имеют противоположные значения, то внутри отрезка найдЁтся такая точка E принадлежащая (a,b), что f(E)=0(теорема хуйзнаеткого).

7.Производная функция и дифференциал. Производная функция-предел отношения приращения функции к приращению независимой переменной, при стремлении последнего к нулю(если этот предел существует). y’=lim ∆y/∆(∆x>0)=lim f(x+∆x)-f(x)/∆x (∆x->0).

f’(x)f’xdy/dxdf/dx. Нахождение произхвожной-это и есть дифференцирование функции. Если функция в точке х₀ имеет конечную производную, то ф-я дифференцируема. Дифференциалом функции называется главная, линейная относительно ∆х, часть приращения функции равная произведению производной на приращение независимой переменной. dy=f’(x)∆x.

8.производные и дифференциалы высших порядков. Производной n-го порядка называется производная от производной от производной (n-1) порядка. f”(x)-второго порядка и т.д. f’”(x)…

Дифференциал nго порядка dⁿy-дифференциал от дифференциала (n-1) порядка этой функции, т.е. dⁿy=d(d^n-1y).Пример:d²y=f’(x)dx². dⁿy=f⁽ⁿ⁾(x)dxⁿ. Дифференциал nго порядка равено произведению произвожной второго порядка(n-го порядка) на n-ю степень дифференциала независимой переменной. f⁽ⁿ⁾(x)=dⁿy/dxⁿ. Пример f”(x)=d²y/dx².

9.геометрический и физический смысл производной и дифференциала, приложения производной в экономических расчЁтах. Производная f’(x₀) есть угловой коэфф. (тангенс наклона) касательной проведЁнной к кривой y=d(x) в точке x_{0 ,} т.е. R=f’(x₀). y-f(x₀)(x-x₀).

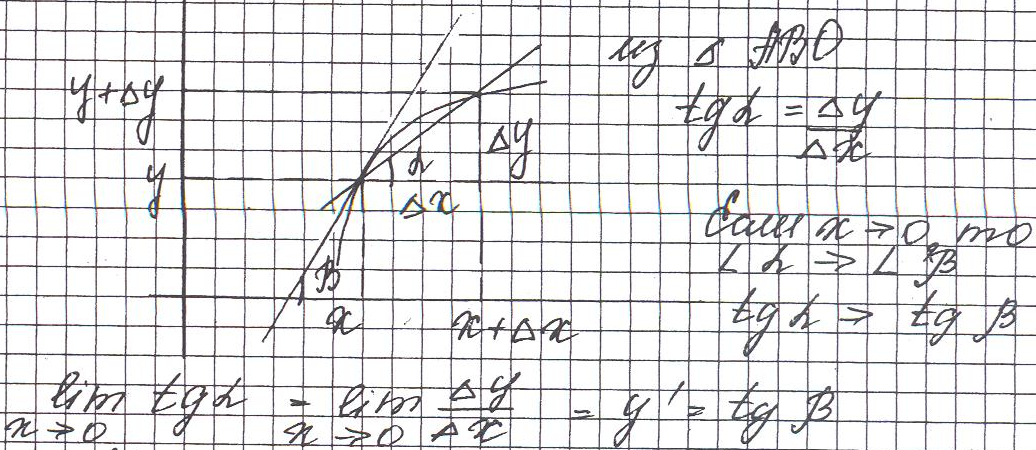
Механический смысл: производная пути по времени S’(t₀) есть скорость точки в момент t₀: v(t₀)=s’(t₀). Дифференциал функции- приращение ординаты касательной, проведЁнной к графику функции y’=f(x) в данной точке, когда x получает приращение ∆х.

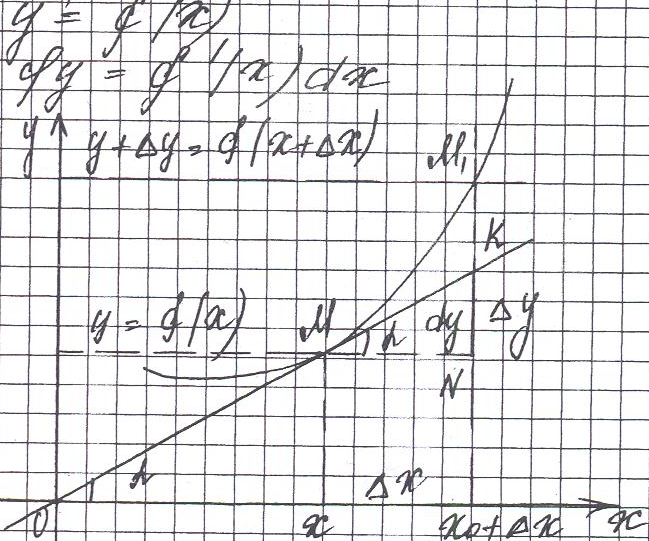
дифференциал функции пути равен расстоянию, которое прошла бы точка за бесконечно малый промежуток времени dx, если бы она двигалась равномерно со скоростью, равной величине мгновенной скорости в момент x.

10.Правила дифференцирования сумм, произведения и частного функций. Производная сложной и обратной функции. Правила дифференцирования: 1.C’=0.2.X’=13.(U+V)’=U’+V’4.(UV)’=U’V+UV’ следствие: 1.(CU)’=CU’. 2.(UVW)’=U’VW+UV’W+UVW’.5.(U/V)’=U’V-UV’/V2.

Сложная функция. Теорема:Если y=f(U) и U=ℓ(x)-дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженный на производную самого промежуточного аргумента и по независимой переменной х, т.е. y’=f’(u)u’.

y=f[u(x)], y=f(u), где y=ℓ(x).

∆y/∆x=∆y/∆u=∆u/∆x

Обратная: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции. X’y=1/Yx.