1. Определение n-мерного вектора. Свойства операция над векторами

N-мерным вектором называется последовательность   чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.

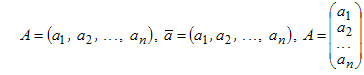
Умножение вектора на число

Любой n-мерный вектор А можно умножить на любое число λ, при этом все его координаты умножаются на это число: λA=(λ*a1, λ*a2,..., λ*an)

Пример: A=(1,2,3); λ=2; A*λ=(1*2,2*2,3*2)=(2,4,6)

Сложение векторов

Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются:

Свойства линейных операций:

• А + В = В + А

• (А + В) + С = А+(В + С)

• λ(А + В) = λА + λВ

• (λ+ μ)А = λА + μ А

• λ(μ А) = (λμ)А

Пример: 

2. Определение скалярного произведения. Свойства скалярного произведения

Скалярное произведение векторов

Скалярным произведением векторов   и   называется величина, вычисляемая по формуле:

Свойства произведения:

• 

• 

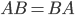
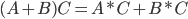
• λ(A*B)=λ*A*B

Пример: 

3. Неравенство Коши-Буняковского. Неравенство треугольника (док-во)

4. Угол между n-мерными векторам. Теорема о равенстве векторов

Угол между векторами

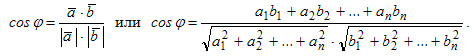
Теорема: Ненулевые n-мерные вектора |A| и |B| равны, когда угол φ между ними равен 0 и |A| и |B| совпадают.

Док-во: A=B (*A)=> AA=AB => AA=BB => √(AA)=√(BB) => |A|=|B|

A=B => AA/|A||A| => A²/ |A|²=1 => φ=0

5. Коллинеарные вектора

A и B коллинеарны, если AˆB=0 или AˆB=π; а) если AˆB=0, одинаково направленные вектора; б) если AˆB=π, противоположно-направленные вектора.

Теорема: Ненулевые вектора A и B коллинеарны, когда можно подобрать такое число K, чтобы B=KA.

6. Разложение вектора по системе векторов. Свойства разложения

Говорят, что вектор B линейно выражается через вектора A1,A2…Ak , если вектор B равен некоторой линейной комбинации векторов A1,A2…Ak , т.е. существует набор чисел такой, что B=L1A1+L2A2+…+LkAk. L1,L2…Lk - коэффициент разложения вектора B по системе векторов A1,A2…Ak.

Ненулевой вектор θ разлагается по любой системе векторов.

Если вектор B разлагается по части системы векторов, то он разлагается по всей системе векторов.

Каждый n-мерный вектор B=(b1,b1…bn) разлагается по диагональной системе n-мерных векторов с коэффициентами, равными координатам вектора B.

7. Элементарные преобразования системы векторов

Система векторов {A1,…Am,B}. Запись в виде матрицы, столбцы которой совпадают с координатами векторов: A1 A2 … Am | B

a1 a2 … am | b1

……………. | …

an an … anm | bn

1. вычеркивание из матрицы нулевой строки

2. умножение j-ой координаты векторов на числа, отличное от 0

3. прибавление к j-ой строки i-ой строки, умноженной на любое число

8. Подобные системы векторов

Если систему векторов A1,A2…Am можно при помощи конечного числа элементарых преобразований превратить в систему B1,B2…Bm

Подобные системы векторов всегда содержат одно и то же число векторов; размерности векторов в этих системах могут не совпадать.

Свойства:

1. Если A1,…Am подобна B1,…Bm, то B1,…Bm подобна A1,…Am

2. Если система А подобна системе В, а система В подобна системе С, то система А подобна системе С

3. Пусть система А подобна системе В. Если нулевой вектор разлагается по системе векторов А, то он разлагается по системе векторов В с теми же коэффициентами.

9. Линейная зависимость систем векторов

A1,A2…Am линейна зависима, если имеется 2 различных разложения нулевого вектора по системе векторов A1,…Am

10. Теорема о разложении вектора по линейно независимой системе векторов. Теорема об условии равносильности линейно зависимой системы векторов.

Теорема: Дана система А, тогда след. условие равносильно:

А) система А линейно зависима/ линейно не зависима

Б) есть ненулевое разложение нулевого вектора по системе А/ есть только нулевое разложение нулевого вектора по системе А

В) хотя бы один из векторов системы А разлагается по остальным/ ни один из векторов системы А не разлагается по остальным векторам этой системы.

11. Базис и ранг системы векторов

Базисом системы векторов называется такая её часть, которая удовлетворяет следующим её условиям:

а) B1,B2,…Br линейно не зависимы

б) каждый вектор системы A1,…Am разлагается по векторам B1,…Br

Рангом системы векторов называется число векторов в любом её базисе

12. Матрица. Квадратная, треугольная и диагональная матрицы

Матрицей типа (или размера) m×n называют прямоугольную числовую таблицу, состоящую из mn чисел, которые расположены в m строках и n столбцах.

Квадратная матрица – матрица, число строк и столбцов которой равна. n=m

Треугольная матрица – матрица, все элементы над главной диагональю равные 0.

Диагональная матрица – все элементы, расположенные вне главной диагонали, равны 0.

13. Умножение матрицы на вектор, на матрицу. Свойства

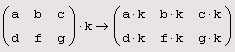
Операция определена, когда координаты вектора столько, сколько же и матрицы.

A_n * B_{n k} = C_k

1 2 3

*

1 3 0 7 4 5

=

13 32

, т.е. 1*1 + 2*0 + 3*4 = 1+0+12 = 13,  1*3 + 2*7 + 3*5 = 3+14+15 = 32.

Свойства:

1. (K+L)A=KA+LA; K,L-векторы, A-матрица

2. (kL)A=k(LA); k-число

3. (LA)K=L(AK); K,L-векторы

14. Умножение матрицы на число и сложение матриц. Свойства

1. Умножение матрицы на число – каждый элементы матрицы умножается на число

2. Сложение матриц – складываются матрицы одинаковой размерности. Складываются элементы стоящие на одинаковых местах.

Свойства:

1. A+B=B+A

2. (A+B)+C=A+(B+C)

3. A(k+l)=Ak+Al

4. A(kl)=(Ak)l=k(Al)

5. (A+B)k=Ak+Bk

15. Умножение матриц. Вычисление строк и столбцов полученной матрицы. Свойства

AxB: произведение определено, если число столбцов A равняется числу строк B.

A (m*n), B(k*l), n=k => C(m*l)

В общем случае произведение матриц непомутативно (множители нельзя переставлять местами)

Свойства:

1. (AB)k=(Ak)B=A(Bk)

2. (A+B)C=AB+AC

3. (AB)C=A(BC)

16. Единичная матрица. Обратная матрица

Пусть A — квадратная матрица порядка n. Квадратную матрицу B того же порядка называют обратной к A, если AB = BA = E, где E — единичная матрица порядка n.

Обратную матрицу обозначают A(−1). Она позволяет определить целую отрицательную степень матрицы A. А именно, для n > 0 полагают A(−n) = (A−1)n.

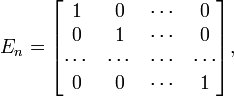
17. Транспонированная матрица. Правила транспонирования

A῟- строки являются столбцами матрицы.

1. Ak=kA῟

2. LA=A῟L

3. (Ak)῟=A῟k

4. (A+B)῟=A῟+B῟

5. (AB)῟=B῟+A῟

18. Ранг матрицы. Преобразования, не меняющие ранг

Ранг – ранг системы её столбцов ( наивысший порядок её отличных от нуля миноров). Элементарные преобразования не меняют её ранга:

1. вычеркивание нулевой строки

2. прибавление к i-ой строке j-ой строки, умноженной на k (i+jk)

3. вычеркивание строки, которая является линейной комбинацией других строк матрицы

4. умножение столбца на отличное от 0 число

19. Теорема о ранге произведения матриц

a) Ранг произведения двух матриц не выше ранга каждого из сомножителей.

b) Ранг произведения произвольной матрицы А справа или слева на невырожденную квадратную матрицу Q равен рангу матрицы А. (C-обратимая матрица, r(AC)=r(A) )

20. Если матрица обратима, то она не вырожденна. Если матрица не вырожденна, то она обратима.

Невырожденная матрица – определитель матрицы не равен 0.

1. Если матрица А обратима, то она не вырожденна. Док-во: Если A и A(-1) – квадратные, то по свойству (определитель произведения квадратных матрицы равен произведению их определителей), имеем 1=detE=det(A*A(-1))=detA(-1)*detA, откуда detA≠0.

2. Если матрица не вырожденна, то она обратима. Док-во:

21. Определитель квадратной матрицы

Определителем n-ого порядка квадратной матрицы A называется алгебраическая сумма элементов, взятых только по одному из каждой строки и каждого столбца, причем, знак каждого слагаемого определяется числом инверсий в перестановках, составленных из 1 и 2 индексов членов сомножителей.

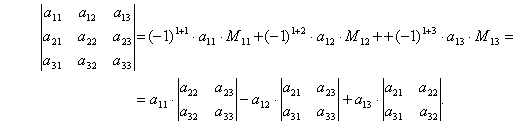
22. Свойства определителя. Док-ва 1,2,3,4,5 и 6 свойств

1. Определитель не меняется при транспонировании.

2. При перестановке любых 2 строк в матрице, определитель меняет знак на обратный.

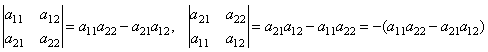
3. Если в определителе есть 2 одинаковые строки, то он равен 0. 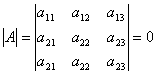Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

4. Если все элементы строки определителя умножить на отличное от 0 число, то определитель умножается на это число (Если элементы какой-либо строки имеют одинаковый множитель, то он выносится за скобки, и определитель матрицы умножается на этот множитель).

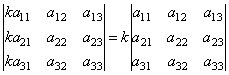
5. Определитель с двумя пропорциональными строками равен 0. Если вынести общий множитель за знак определителя у одной из пропорциональных строк, чтобы в определителе получилось 2 одинаковые строки, то по св.3 величина определителей равна 0.

6. Определитель, содержащий нулевую строку, равен 0. Доказывается проверкой.

7. Если каждый элемент какой-либо строки определителя представлен в виде суммы двух слагаемых, то его можно представить в виду суммы двух определителей.

8. Определитель не изменится, если к элементам любой его строки прибавить элементы любой другой строки, умноженные на одно и то же число.