23. Разложение определителя по строке и столбцу

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

d = a_{i 1} A_{i 1} + a_{i 2} A_{i 2} +... + a_{i n} A_{i n}   (i =  )

или j- го столбца

d = a_{1 j} A_{1 j} + a_{2 j} A_{2 j} +... + a_{n j} A_{n j}    (j =  ).

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

24. Совместные слу. Теорема Кронеккера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение( совместная система лин. уравнений является определенной тогда и только тогда, когда ранг основной матрицы системы уравнений равен рангу расширенной), и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

25. Теорема Крамера

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

RgA = RgA^*.

            Очевидно, что система (1) может быть записана в виде:

x₁ + x₂ + … + x_n

            Доказательство.

            1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.

            2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

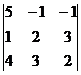 =   = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

1 =    = (28 – 48) – (42 – 32) = -20 – 10 = -30.

x1 = D1/D = 1; 2 =    = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

x2 = D2/D = 2; 3 =    = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.

26. Определение общего решения слу. Базисные и свободные неизвестные.

Общее решение системы — совокупность всех частных решений системы.

Частное решение системы — одно из решений неопределенной совместной системы.

27. Однородные слу. Свойства однородной слу. Теорема о нулевом и ненулевом решении слу,

Однородная система — система, у которой все свободные члены равны нулю.

Однородная система — всегда совместна, так как x₁=x₂=x₃=...=x_n=0 является решением системы.

Теоремы о ненулевых решениях однородной системы :

• Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r<n.

Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что   не превосходит  . В случае   система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при  .

Следствие 1: Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.

Доказательство: Если у системы уравнений  , то ранг   системы не превышает числа уравнений  , т.е.  . Таким образом, выполняется условие   и, значит, система имеет ненулевое решение.

Следствие 2: Однородная система   уравнений с   неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.

Доказательство: Допустим, система   линейных однородных уравнений, матрица которой   с определителем  , имеет ненулевое решение. Тогда по доказанной теореме  , а это значит, что матрица   вырожденная, т.е. 

• Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель D был равен нулю, т. е. D=0.

28. Теорема о числе линейно независимых решений однородной СЛУ

Число линейно-независимых решений однородной СЛУ не превосходит числа n-r(A).

29. Фундаментальная система решений однородной СЛУ

Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.

Система F1,F2…Fk называется ФСР, если выполняются условия:

а) вектора F1,F2..Fk линейно-независимы

б) k=n-r(A) – число решений равно разности количества неизвестных и ранга системы

30. Теорема об условии существования ФСР однородной СЛУ

Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.

31. Общее решение СЛУ в векторной форме

Рассматривается совместная система линейных уравнений AX=B. Если положить B=Ѳ, то получим следующее: AX= Ѳ – такая система является приведенной формы для AX=B. Если K является решением системы AX=B, то вектор B можно разложить по столбцам: B=A1K1+A2K2+…+AnKn

Теорема: Произвольное решение X совместной системы уравнения AX=B определяется формулой: X=K+t1F1+t2F2+…+tkFk, где K – решение системы AX=B, F1,…Fk – ФСР уравнения AX= Ѳ, а t1,t2…tk – произвольные действительные числа