3.Понятие числовой последовательности и основные свойства сходящихся последовательчностей.

Если по некоторому закону каждому натуральному числу n поставлено в соответствии вполне определенное число ,то говорят, что задана числовая последовательность :

Другими словами, числовая последовательность-это функция натурального аргумента . Числа наз. Членами последовательности, а число общим или n-ым членом последовательности.

Последовательность, имеющая предел, наз. сходящейся, в противном случае-расходящейся.

Св-ва: Пусть имеются 2 последовательности

1. Если =а, то

2. Сходящаяся последовательность ограничена.

3. Если , 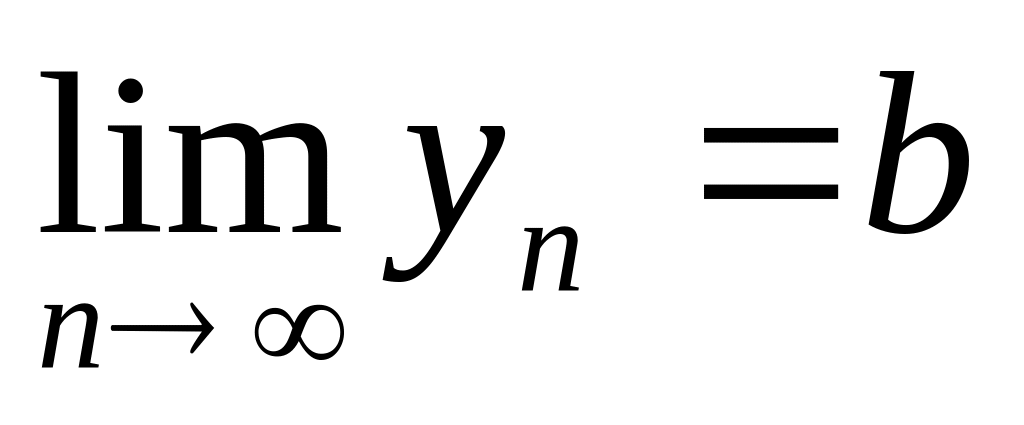,тогда

4. 

5. ,B 0.

6. Если 2 последовательности имеют одинаковый предел и есть последовательность, находящаяся между ними, то она будет иметь тот же предел.

4. Предел числовой последовательности. Признаки существования предела последовательности. Два замечательных предела.

Число А называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа >0, найдется такой номер N, что для всех членов последовательности с номерами n>N верно неравенство: . Пердел числовой последовательности обозначается .

Признаки существования предела: 1) Если числовая последовательность монотонна и ограниченна, то она имеет предел.

2) Если в некоторой окрестности точки функция f(x) заключена между двумя функциями , имеющими одинаковый предел А при , то функция f(x) имеет тот же предел А.

Замечательные пределы: Первым замечательным пределом называется

Вторым замечательным пределом (число е) называется предел числовой последовательности ,где е-число Эйлера.

5.Предел функции в бесконечности и в точке.

Число А называется пределом функции у=f(x) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число S>0, что для всех х таких, что >s, верно неравенство предел функции обозначается

Число А называется пределом функции f(x) при х, стремящемся к (или в точке ), если для любого даже сколь угодно малого положительного числа >0, найдется такое положительное число >0, что для всех х, не равных и удовлет.условию ,этот предел обозначается .

Замечание 1. Определение предела не требует существования функции в самой точке .

6. Непрерывность функции действительной переменной в точке и на отрезке. Свойства функций, непрерывных на отрезке.

Функция f(x) называется непрерывной в точке ,если она удовлетворяет след.трем условиям: 1)определена в точке (т.е. существует f( )); 2) имеет конечный предел функции при ;3) этот предел равен значению функции в точке ,т.е.

Функция y=f(x) называется непрерывной в точке ,если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

Св-ва функций, непрерывных на отрезке:

1. Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.

2. Если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М.

3. Если функция у=f(x) непрерывна на отрезке [a,b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка найдется точка такая, что f( )=0/

7. Производная функции и дифференциал.

Производной функции у=f(x) наз.предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю( если этот предел существует): .

Нахождение производной функции наз. Дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция наз. Дифференцируемой в этой точке.

Если функция у=f(x) дифференцируема в точке , то она в этой точке непрерывна. (непрерывность функции-необходимое, но недостаточное условие дифференцируемости функции.)

Дифференциалом функции наз. Главная, линейная относительно часть приращения функции, равная . Dy=dx=

Dy= .

Дифференциал равен приращению ординаты касательной в данной точке, когда х получает приращение .

Св-ва дифференциала: 1)d(cf)=cdf, c=const. D(cf)=

2)d(f

3)d(f

4)d(f/ .