3.3. Распределенность терминов в суждении.
Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема. Рассмотрим распределение терминов в суждениях A, E, I, O.
A (все S суть P ): «Все студенты нашей (S) группы сдали экзамены (P)». В данном суждении S - субъект взят в полном объеме (распределен), P – часть лиц, сдавших экзамены (не распределен), в это количество могут входить и другие группы студентов.
E (ни одно S не есть P): «Ни один студент нашей группы (S) не является неуспевающим (P)». И S, и P взяты в полном объеме, то есть распределены.
I (некоторые S суть P): «Некоторые студенты нашей группы – спортсмены». S – не распределен, так как мыслится часть студентов, объем S частично входит в объем предиката, поэтому ни S, ни P не распределены.
O (некоторые S не суть P): «Некоторые студенты нашей группы – не спортсмены». S – не распределен, P – распределен.
ТАБЛИЦА РАСПРЕДЕЛЕННОСТИ ТЕРМИНОВ
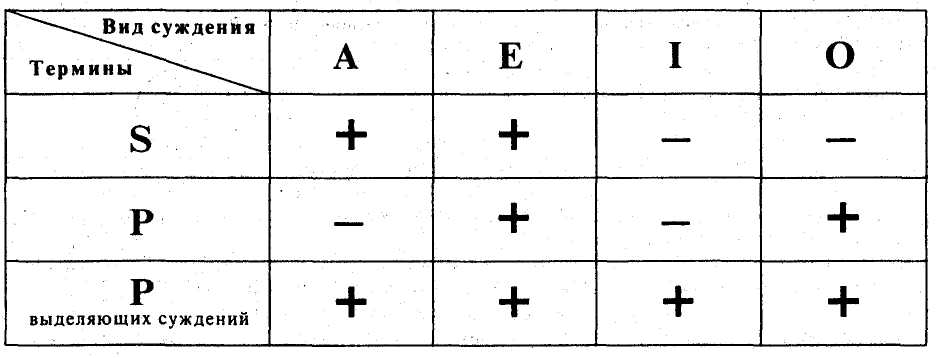
Субъект распределен в общих (А и Е) и не распределен в частных суждения (I и О).
Предикат распределен в отрицательных (Е и О) и не распределен в утвердительных суждениях (А и I)
В выделяющих суждениях предикат распределен.
Обозначения: + - распределенность термина
— - нераспределенность термина
ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ
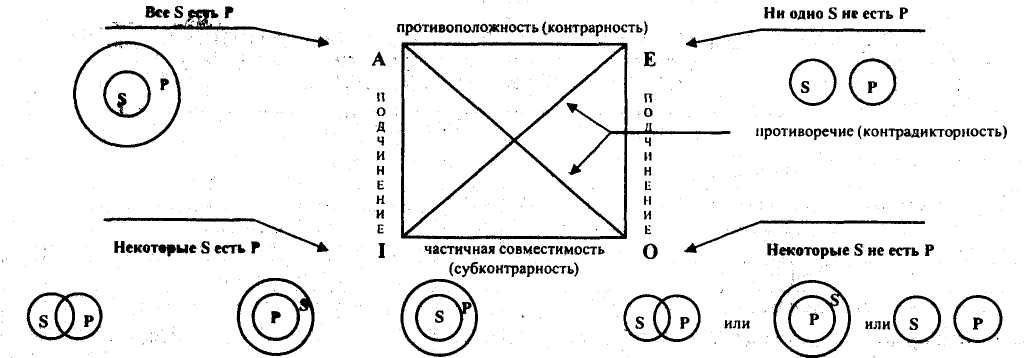
Логический квадрат
Логическому
квадрату эквивалентна таблица 1,
иллюстрирующая
функциональна-истинностные отношения
между высказываниями вида А,Е,1,О.
Из таблицы 1 высказывания А и Е не могут быть одновременно истинными, но могут быть одновременно ложными. В этом смысле всякое высказывание вида А контрарно соответствующему высказыванию вида Е.
Аналогичным образом с помощью таблицы 1 легко понять отношение субконтрарности между высказываниями вида I, О и отношение подчинения между высказываниями вида А, I (а также вида Е,О).
3.4. Сложные суждения.
Сложным называют суждение, включающее в качестве составных частей другие суждения, связанные логическими связками – конъюнкцией, дизъюнкцией, импликацией и или эквивалентностью (, , , ). В зависимости от логической связки различают следующие виды сложных суждений: соединительные, разделительные, условные и эквивалентные.
I. Соединительное (конъюнктивное) суждение – это суждение, включающее в качестве составных частей другие суждения – конъюнкты, объединяемые связкой «и». Например: «Иванов (p) и Сидоров (q) являются студентами». pq. Конъюнкция () обладает свойством коммутативности или перестановочности (смысл суждения не меняется от перестановки). Истинность соединительного суждения зависит от истинности его конъюнктов. Условия истинности показаны в таблице.
-
p
q
pq
и
и
и
и
л
л
л
и
л
л
л
л
Истинность и ложность многосоставных конъюнктивных суждений определяется правилом: конъюнкция истинна в случае истинности всех ее членов и ложна при ложности хотя бы одного из ее членов.
Грамматически конъюнктивная связка выражается союзом «и», «но», «также», «как», «так и», «хотя», «однако», «несмотря на», «вместе с тем» и др.
II. Разделительное (дизъюнктивное) суждение – это суждение, включающее в качестве составных частей суждения-дизъюнкты, разъединяемые связкой «или». Например: «Курсовая работа может быть сдана (p) в письменном или устном виде (q)». pq.
Дизъюнкция обладает свойством коммутативности, АВ тоже, что и ВА, и свойством ассоциативности, то есть изменение членов разделительного суждения не меняет смысла суждения, то есть (АВ)С или А(ВС), или АВС.
Истинность разделительного суждения определяется истинностью составляющих его дизъюнктов. Связка «или» употребляется в двух значениях: соединительно-разделительном и исключающе-разделительном. Различают два типа разделительных суждений:
Нестрогая дизъюнкция – суждение, в котором связка «или» употребляется в соединительно-разделительном значении (символ ). Условия истинности нестрогой дизъюнкции представлены в таблице.
-
p
q
pq
и
и
и
и
л
и
л
и
и
л
л
л
Суждение pq истинно при истинности хотя бы одного из членов дизъюнкции, и ложна при ложности всех членов. Например: «По форме правления современное государство может быть республикой либо монархией». pq
Строгая дизъюнкция – суждение, в котором связка «или» употребляется только в разделительном значении (символ ). Например: «Деяние может быть умышленным или неосторожным». Члены строгой дизъюнкции называются альтернативами, они не могут быть одновременно истинными.
-
p
q
pq
и
и
л
и
л
и
л
и
и
л
л
л
Суждение pq будет истинно при истинности одного и ложности другого члена. Суждение pq будет ложным, если оба члена истинны или оба ложны. Многосоставное суждение строгой дизъюнкции будет истинным при истинности лишь одной альтернативы, и ложным при одновременной ложности, так и при одновременной истинности всех альтернатив. Разделительная связка в языке выражается с помощью союзов «или», «либо», для строгой дизъюнкции – «или-или», «либо-либо».
III. Условные (импликативные) суждения – это суждение, включающее в качестве составных два суждения – антецедент и консеквент, объединяемые связкой «если …, то…». Например: «Если предохранитель расплавится (условие), то лампа погаснет (обусловленное». Если p, то q. pq. Импликация ложна только при истинности антецедента и ложности консеквента, в других случаях она истинна.
-
p
q
pq
и
и
и
и
л
л
л
и
и
л
л
и
IV. Эквивалентные суждения (двойная импликация) – это суждения, состоящие из двух и более простых суждений, связанных двойной (прямой и обратной) условной зависимостью, выражаемой связкой «если и только если …, то …». Можно рассматривать его как необходимое и достаточное условие для какого-либо утверждения. Выражается знаком и читается: если и только если p, то q. Суждение pq истинно тогда, когда оба суждения являются либо истинными, либо ложными.
-
p
q
pq
и
и
и
и
л
л
л
и
л
л
л
и
Сводная таблица истинности сложных суждений.
-
p
q
pq
pq
pq
pq
pq
и
и
и
и
л
и
и
и
л
л
и
и
л
л
л
и
л
и
и
и
л
л
л
л
л
л
и
и