2.1.3 Признаки вейвлета

Для практического применения важно знать признаки, которыми обязательно должна обладать функция, чтобы быть вейвлетом; приведём их здесь, а также рассмотрим в качестве примеров некоторые хорошо известные функ­ции и их соответствие этим необходимым признакам.

Локализация. Вейвлет-преобразование в отличие от преобразования Фурье использует локализованную базисную функцию. Вейвлет должен быть локализован и во временном пространстве, и по частоте.

Нулевое среднее:

Часто для приложений оказывается необходимым, чтобы не только нулевой, но и все первые моментов были равны нулю:

Такой вейвлет называется вейвлетом -го порядка. Обладающие большим числом нулевых моментов вейв­леты позволяют, игнорируя наиболее регулярные поли­номиальные составляющие сигнала, анализировать мел­комасштабные флуктуации и особенности высокого порядка.

Ограниченность:

Оценка хорошей локализации и ограниченности может быть записана в виде

или

здесь  доминантная частота вейвлета, число должно быть возможно большим.

Автомодельность базиса. Характерным признаком базиса вейвлет-преобразования является его самоподо­бие. Все вейвлеты данного семейства имеют то же число осцилляции, что и базисный вейвлет , по­скольку получены из него посредством масштабных преобразований и сдвигов. Благодаря этому вейвлет-преобразование с успехом применяется для анализа фрактальных сигналов.

Например, -функция и синус не удовлетворяют необходимому условию одновременной локализации во временном пространстве и в пространстве частот: хорошо локализованная в -пространстве -функция не обладает этим свойством в -пространстве; наоборот, хорошо локализованный в -пространстве синус не обладает этим свойством в -пространстве.

Функция Габора

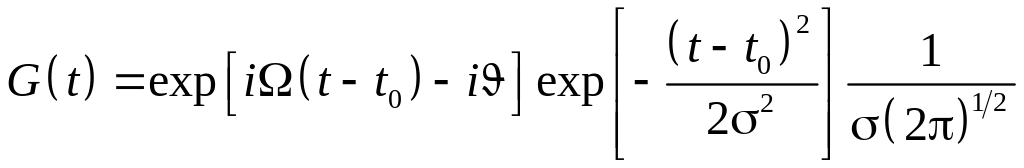
представляет собой модулированную функцию Гаусса с четырьмя параметрами: сдвиг , стандартное (средне­квадратичное) отклонение , частота модуляции и фазовый сдвиг . Разложение по функциям Габора является разложением по модулированным фрагментам синусоид. Длина фрагментов для всех частот постоянна, что даёт различное число осцилляции для разных гармо­ник. Отсюда следует, что достаточно хорошо локализо­ванная и в -, и в -пространстве функция Габора не может быть базисной функцией вейвлет-преобразования, поскольку построенный на её основе базис не обладает свойством самоподобия.

HAAR-вейвлет (1.11)  пример ортого­нального дискретного вейвлета, порождающего ортонормированный базис. Недостатками этого вейвлета являются негладкость  резкие границы в -пространстве, вследствие чего возникают бесконечные (убываю­щие как «хвосты» в -пространстве, а также несим­метрия формы. Для некоторых приложений эти недо­статки несущественны, а иногда односторонность вейвлета даже становится достоинством.

Часто приме­няется очень похожий, также дискретный, но симметрич­ный FHAT-вейвлет, более известный под названием «Французская шляпа» (похожа на цилиндр) (French hat):

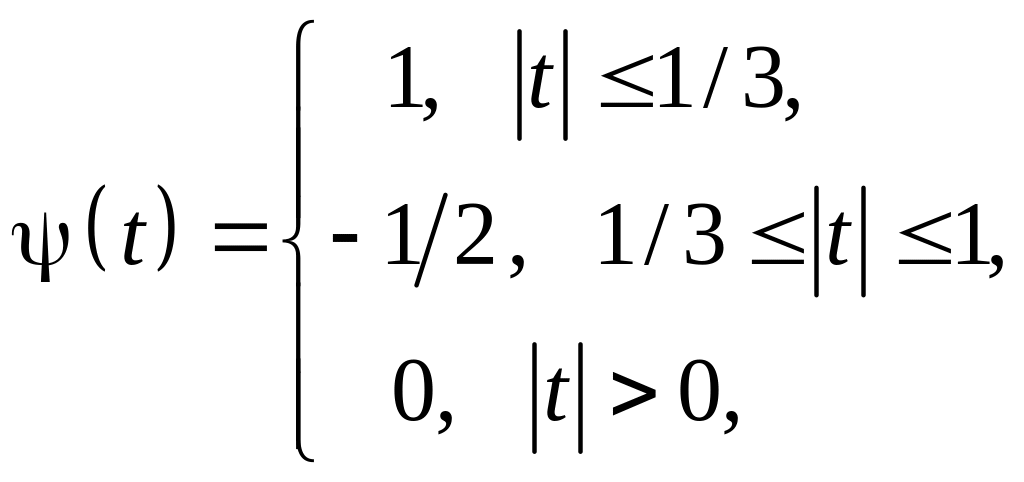
здесь  функция Хевисайда при k > 0 и при k  0).

FHAT-вейвлет, нерегулярный во временном про­странстве и недостаточно быстро спадающий в про­странстве частот, и LP-вейвлет (вейвлет Литтлвуда-Пэли (Littlewood & Paley)), наоборот, имеющий резко очерченные границы в -пространстве и плохо спадающий в -пространстве, можно считать предель­ными случаями, между которыми находятся практически все вейвлеты.