1.2 Разложение по вейвлетам

Дискретные преобразования. С помощью быстро стремящейся к нулю локализованной функции, предусмотрев систему сдвигов (переносов) вдоль оси, покрывается вся ось . Пусть для простоты смещение по оси времени будут целыми числами, т.е. . Введём аналог синусоидальной частоты. Для про­стоты и определённости запишем её через степени двойки: , здесь и  целые числа .

Таким образом, с помощью дискретных масштабных преобразований и сдвигов мы можем описать все частоты и покрыть всю ось, имея единствен­ный базисный вейвлет .

Напомним определение нормы:

(звёздочка обозначает комплексно-сопряжённую функцию). Следо­вательно,

т.е. если вейвлет имеет единичную норму, то все вейвлеты семейства вида

(1.9)

также нормированы на единицу, т.е.

Вейвлет называется ортогональным, если определённое соотношением (1.9) семейство предста­вляет собой ортонормированный базис функциональ­ного пространства , т.е.

и каждая функция может быть представлена в виде ряда

, (1.10)

равномерная сходимость которого в означает, что

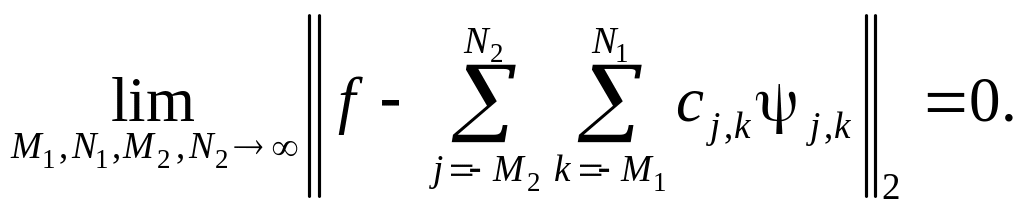
Простейшим примером ортогонального вейвлета является HAAR-вейвлет, названный так по имени пред­ложившего его в 1910 г. Хаара (Нааr) и определяемый соотноше­нием

(1.11)

Легко видеть, что любые две функции получен­ные из этого вейвлета по формуле (1.9) с помощью масштабных преобразований и сдвигов , ортогональны и имеют единичную норму.

Сконструируем базис функционального простран­ства с помощью непрерывных масштабных преоб­разований и переносов вейвлета с произвольными значениями базисных параметров  масштабного коэф­фициента и параметра сдвига :

(1.12)

На его основе запишем интегральное вейвлет-преобра­зование:

(1.13)

Проводя дальнейшую аналогию с преобразованием Фурье, коэффициенты разложения (1.10) функ­ции в ряд по вейвлетам можно определить через интегральное вейвлет-преобразование:

(1.14)

В дальнейшем иногда вместо для коэф­фициентов (амплитуд) вейвлет-преобразования исполь­зуются обозначения или , или .

Каждая функция из может быть получена суперпозицией масштабных преобразовании и сдвигов базисного вейвлета, т.е. является композицией «вейвлетных волн» (с коэффициентами, зависящими от номера волны (частоты, масштаба) и от параметра сдвига (времени)).

Использование дискретного вейвлет-преобразования (дискретного частотно-временного пространства в виде целых сдвигов и растяжений по степеням двойки) позво­ляет провести доказательство многих положений теории вейвлетов, связанных с полнотой и ортогонально­стью базиса, сходимостью рядов и т.п. Доказательность этих положений необходима, например, при сжатии информации или в задачах численного моделирования, т.е. в случаях, когда важно провести разложение с минимальным числом независимых коэффициентов вейвлет-преобразования и иметь точную формулу обрат­ного преобразования. При применении вейвлетов для анализа сигналов непрерывное вейвлет-преобразование (1.13) более удобно; его некоторая избыточность, связан­ная с непрерывным изменением масштабного коэффи­циента и параметра сдвига , становится здесь положи­тельным качеством, так как позволяет более полно и чётко представить и проанализировать содержащуюся в данных информацию.

Итак, вейвлет-коэффициенты определяются интегральным значением скалярного произведения сигнала на вейвлет-функцию заданного вида.

Прямое вейвлет-преобразование (ПВП), именуемое также непрерывным преобразованием, означает разложение произвольного входного сигнала на принципиально новый базис в виде совокупности волновых пакетов  вейвлетов,  которые характеризуются четырьмя принципиально важными свойствами: • имеют вид коротких, локализованных во времени (или в пространстве), волновых пакетов, с нулевым значением интеграла; обладают возможностью сдвига по времени; способны к масштабированию (сжатию/растяжению); имеют ограниченный (или локальный) частотный спектр.

Этот базис может быть ортогональным, что заметно облегчает анализ, даёт возможность реконструкции сигналов и позволяет реализовать алгоритмы быстрых вейвлет-преобразований. Однако, есть ряд вейвлетов, которые свойствами ортогональности не обладают, но которые, тем не менее, практически полезны, например, в задачах анализа и идентификации локальных особенностей сигналов и функций.

При вейвлет-преобразовании выбор типов вейвлетов намного более обширен, чем при преобразовании Фурье. В качестве вейвлет-функций могут использоваться ортогональные, биортогональные и полуортогональные непериодические функции, функции, имеющие глобальный экстремум и быстрое затухание на бесконечности (см. подразделы 2.1.1, 2.1.2 лекции 2) и т.д. Все это даёт обширные возможности для представления различных сигналов.