3.4 Нормирование

В дальнейшем нам будет удобно работать с нормированными масштабирующими функциями и вейвлетами. Определим норму вектора в евклидовом пространстве следующим об­разом

Вектор и в евклидовом пространстве называется нормиро­ванным, если Нормированный вектор u может быть получен из любого ненулевого вектора путём деления вектора на его норму:

Таким образом, чтобы нормировать и , нам нужно оп­ределить их нормы:

Таким образом, для каждого и аналогично для каждого . Итак, для того, чтобы работать с нормирован­ными масштабирующими функциями и вейвлетами, необхо­димо переопределить их. Для этой цели мы определим как:

a определим как

(3.16)

Будем называть вейвлеты, заданные равенством (3.16) (где определяется равенством (3.11)) нормированными вейвле­тами Хаара.

3.5 Вейвлет-преобразование

Предположим, что мы имеем последовательность, состоящую из точек для некоторого целого n > 0.

Мы можем отождествить эту последовательность со сле­дующей функцией из Vⁿ:

(3.17)

Первым шагом вычисления вейвлет-преобразования после­довательности будет разложение по альтер­нативному базису пространства вида (2.15), половину ко­торого составляют вейвлеты:

(3.18)

Коэффициенты при базисных вейвлет-функциях составляют половину коэффициентов вейвлет-преобразования, поэтому мы сохраним эти значения. Сле­дующим шагом процесса преобразования является применение такого же базисного преобразования к остальным членам равенства (3.18):

(3.19)

Таким образом, это элемент , и поэтому может быть разложен по альтернативному базису» состоящему из мас­штабирующих функций и вейвлетов

Прежде чем мы продолжим этот процесс, зададим один на­прашивающийся вопрос: как мы получаем коэффициенты равенства (3.18) из коэффициентов равенства (3.17)? Для этого мы используем ортогональность. Напомним, что каж­дая ортогональна каждой так же как и всем , и, аналогично, каждый вейвлет ортогонален другим вейвлетам и всем масштабирующим функциям . На­помним также, что каждая и каждый являются нор­мированными в силу тождеств и . Чтобы вос­пользоваться этой ортогональностью и нормированностью, умножим обе части (3.18) на и проинтегрируем по от 0 до 1. В результате получим

. (3.20)

В силу ортогональности в правой части (3.20) остаётся толь­ко один член, а нормирование приводит к отсутствию коэф­фициента при . Теперь подставим правую часть равенст­ва (3.17) вместо в (3.20). Например, при j = 0 левая часть равенства (2.20) будет равна

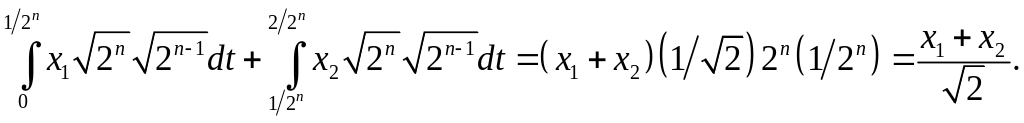(3.21)

Комбинируя (3.20) и (3.21) при j = 0, получим

(3.22)

Квадратный корень в коэффициенте в (3.21) появляется за счёт нормирования. Если бы мы использовали ненормиро­ванные базисные функции, то мы бы получили двухточечное среднее значение. Ос­тальные коэффициенты вычисляются ана­логично. Таким образом,

(3.23)

Аналогично, используя свойства ортогональности и норми­рованности функций можно вычислить коэффициенты по следующей формуле

(3.24)

Ещё раз напомним, что квадратный корень в выражении для коэффициента (3.24) появляется в результате нормирования. Без нормирования мы бы имели только разность выражений.

Еще раз напомним, что квадратный корень в выражении для коэффициента (3.48) появляется в результате нормирования. Без нормирования мы бы имели только разность выражений, полученную в подразделе 3.3. Уравнения (3.47) и (3.48) удобно представить в виде одного матричного уравнения:

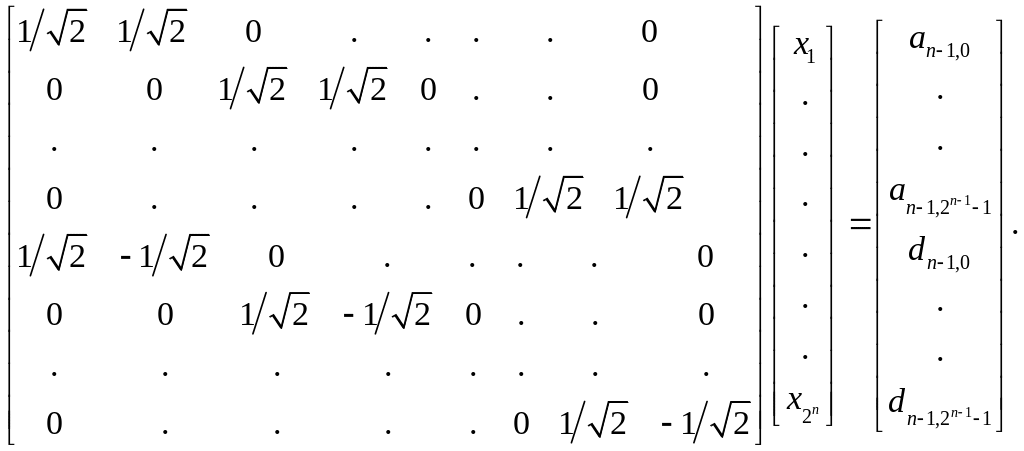(3.25)

Матрица в (3.25)  это квадратная матрица с 2ⁿ строками и 2 ⁿ столбцами. Определим

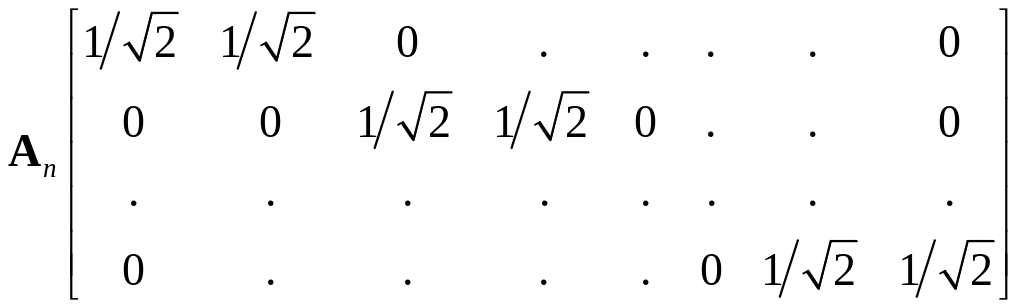(3.26)

и

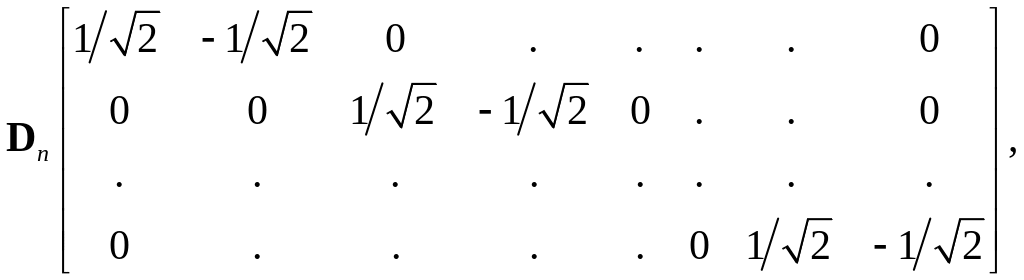(3.27)

где матрицы размером 2^n1  2ⁿ, и можно рассматривать как оператор усреднения и : опе­ратор разности. Введем также векторную запись

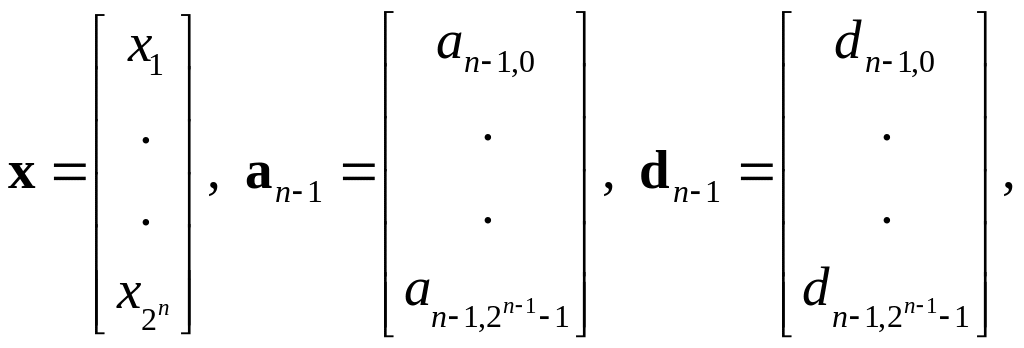
где х  это вектор-столбец с 2ⁿ элементами, а  век­торы-столбцы с 2^n1 элементами. Тогда мы можем переписать (3.25) как

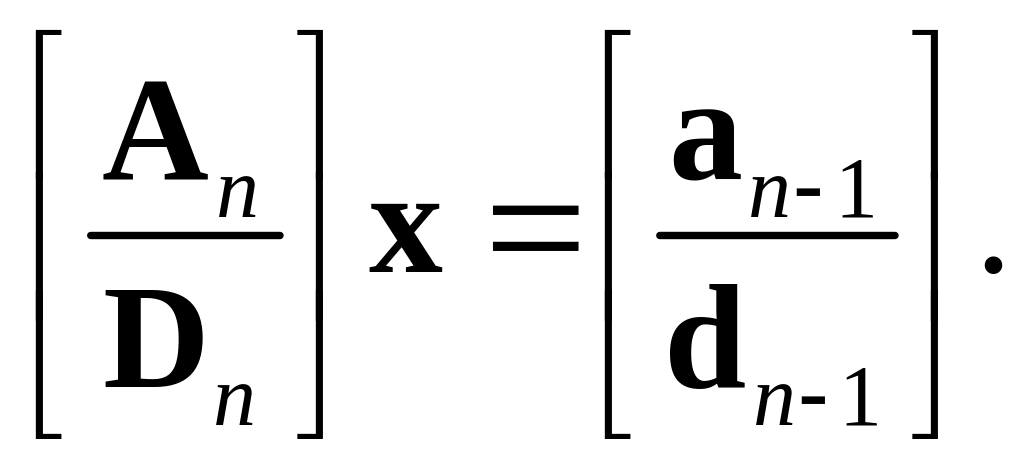(3.28)

Матрица в левой части (3.28)  это единая матрица 2ⁿ  2ⁿ, а вектор в правой части  единый вектор-столбец 2ⁿ 1. На каждом шаге процесса вейвлет-преобразования мы сохраня­ем детализирующие коэффициенты и обрабатываем коэффициенты усреднения. В рассматриваемом случае вейвлет-преобразование будет иметь 2ⁿ компонентов. Половину из них мы получаем из уравнения (3.28) в качестве детализи­рующих коэффициентов в Сохраняем эти коэффициенты как половину вейвлет-преобразования. Следующий шаг вейвлет-преобразования состоит в применении к опера­ций усреднения и вычитания на следующем, более низком уровне разрешения:

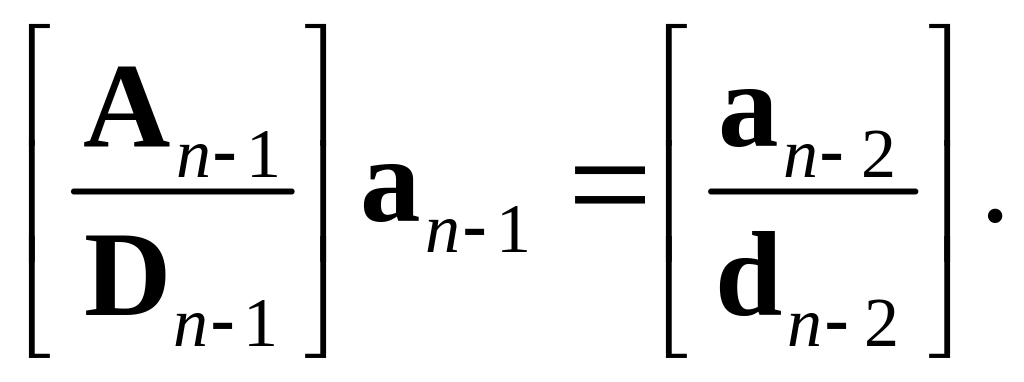
Здесь это 2^n2  2^n1 матрицы вида (3.26) и (3.27), а это векторы-столбцы размерности 2^n2.

Чтобы построить часть вейвлет-преобразования, мы сохра­ним вместе с Продолжим этот процесс, применяя операции усреднения и вычитания к и сохраняя получен­ные детализирующие коэффициенты как часть вейвлет-преобразования. На заключительном шаге сохраним среднее значение которое является однокомпонентным вектором (т.е. скаляром) с единственным элементом Результирующее вейвлет-преобразо- вание, которое мы можем представить как единый вектор-столбец с 1 + 1 + 2 +...+ 2^n1 = 2ⁿ элементами, будет иметь вид:

(3.29)

Пример использования обратного вейвлет-преобразования последовательности точек. Чтобы вейвлет-преобразование могло быть использовано в приложениях, таких, например, как сжатие изображений, оно должно быть обратимым. То есть, при заданном вейвлет-преобразовании вида (3.29), мы должны восстановить исходную последовательность из которой было получено преобразование. Фактически, в подразде­ле 3.1 было проделано это обратное преобразование. Сейчас проделаем аналогичные действия. Шаг вейвлет-преобразования, заключающийся в переходе от k уровня разрешения к выглядит следующим образом:

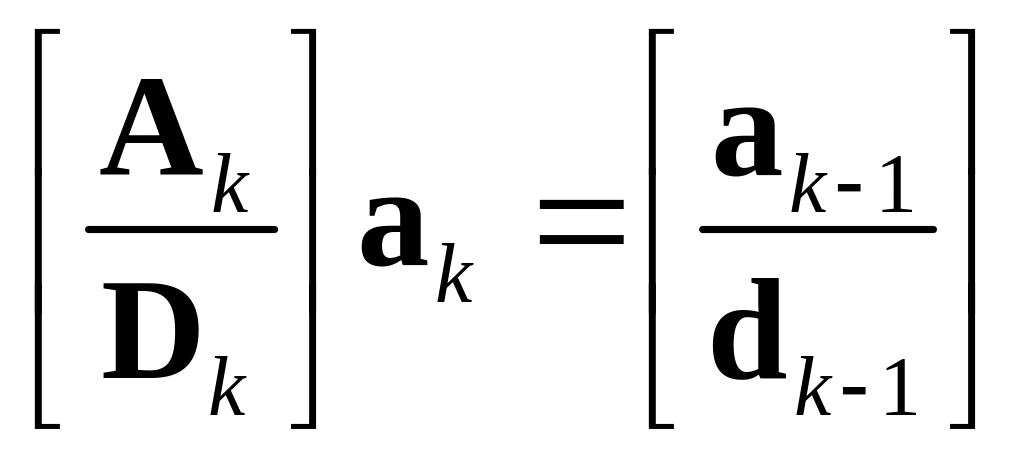(3.30)

откуда мы получаем

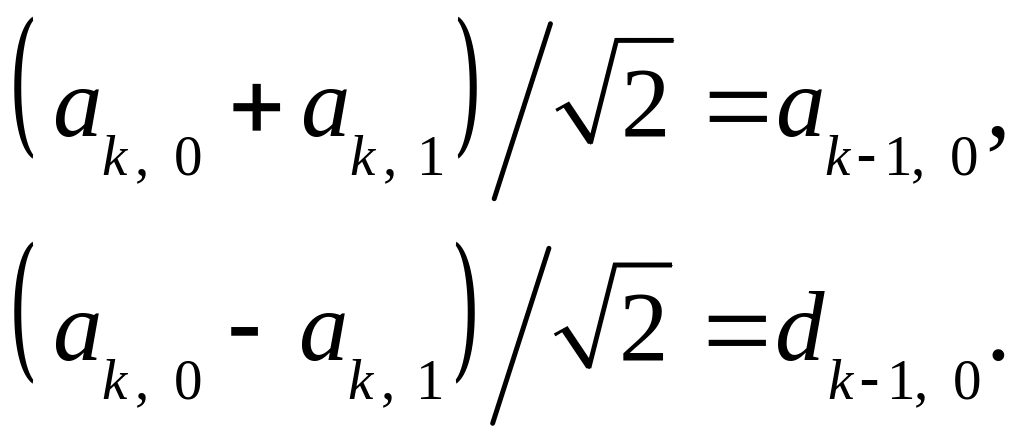(3.31)

Заметим (это понадобится для дальнейших ссылок), что (3.30) и (3.31) могут быть записаны в виде пары матрично-векторных уравнений:

(3.32)

для каждого k = 1, ..., n,

Из (3.31) мы, по известным выражениям для более низкого уровня разрешения и , можем легко найти выраже­ния для более высокого уровня разрешения

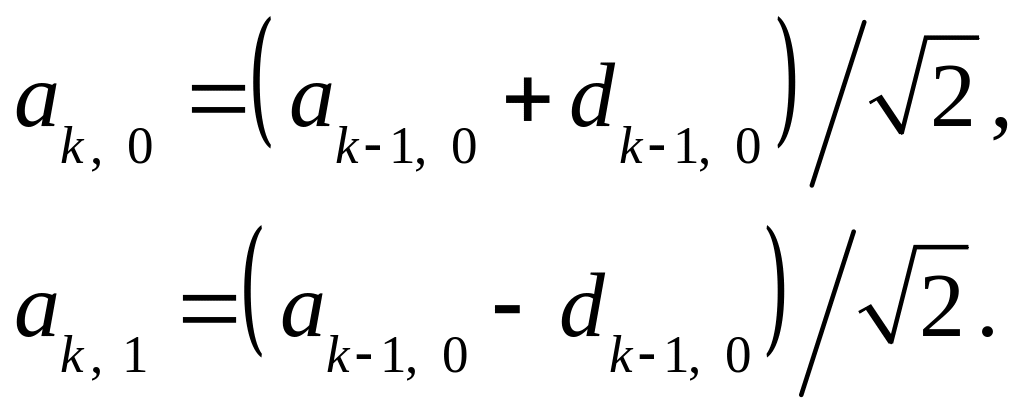
Аналогично, для j = 0, ..., 2^k1,

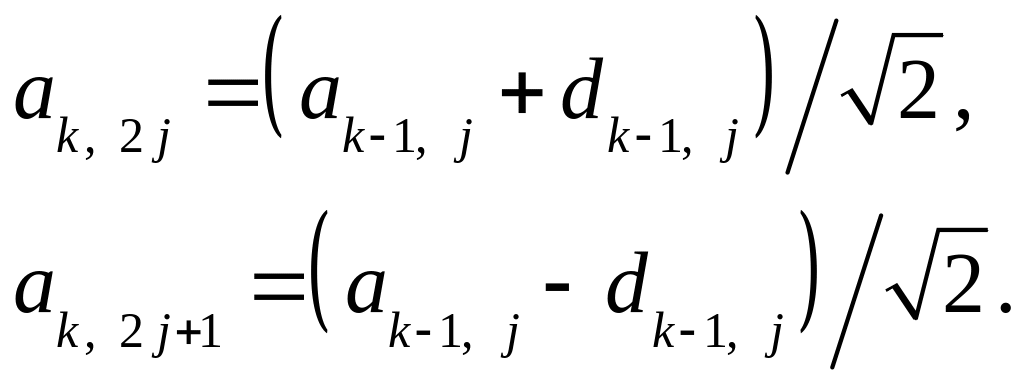(3.33)

С точки зрения линейной алгебры мы разрешили уравнение (3.30) относительно вектора путем обращения матрицы левой части этого уравнения. Таким образом, мы выполнили следующую операцию:

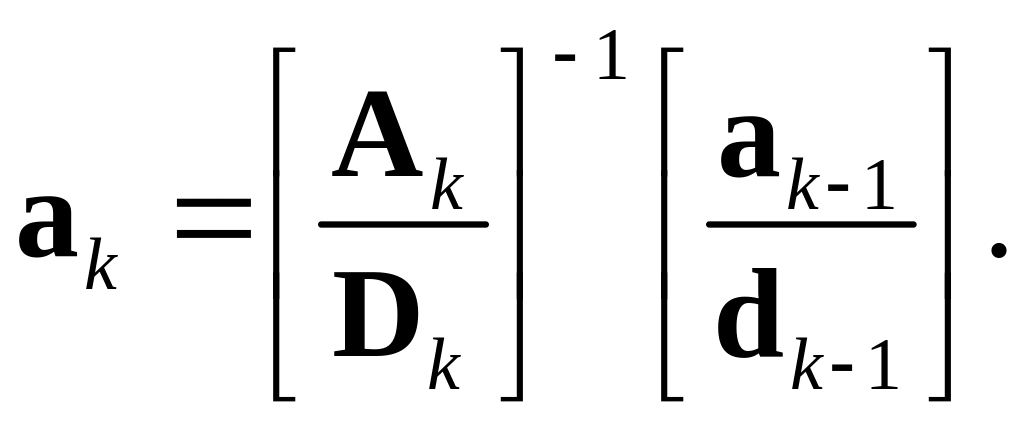(3.34)

Откуда мы знаем, что обратная матрица в (3.34) существует? Потому что мы находим ее в (3.33). В матричной форме это обращение выглядит как

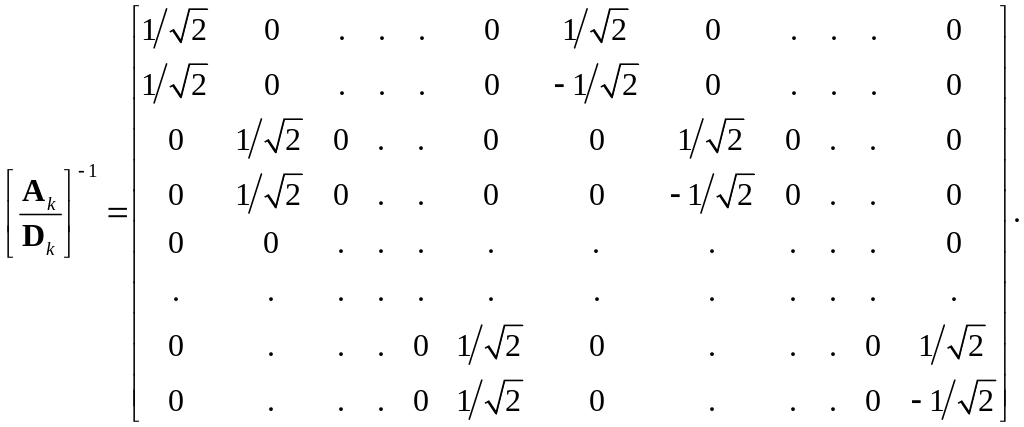(3.35)

Сравнение с (3.25) показывает, что эта обратная матрица яв­ляется всего лишь транспонированной по отношению к мат­рице прямого преобразования. Фактически первые столб­ца матрицы в (3.35) в точности представляют собой транс­понированную матрицу а последние столбца  транс­понированную матрицу Это удобное свойство возникает благодаря ортогональности и нормированности наших ба­зисных функций масштаба и вейвлет-функций. Таким обра­зом, мы можем записать обращение в (3.35) как:

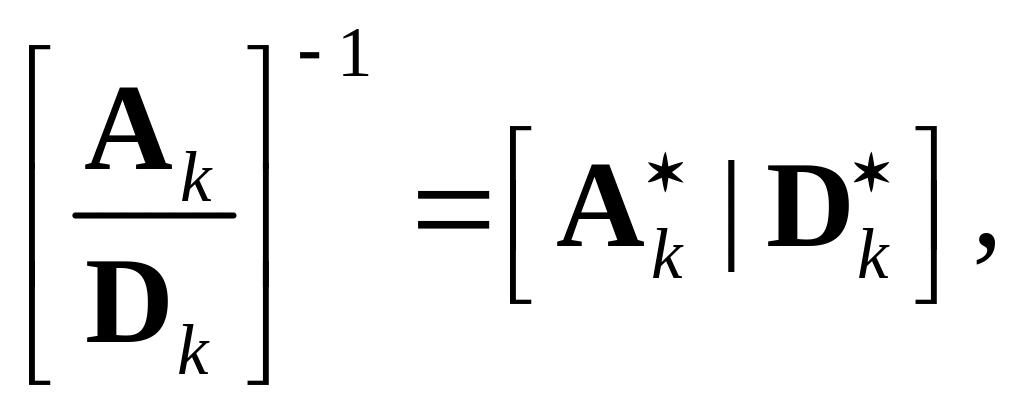
где * обозначает транспонирование матрицы. Теперь мы можем переписать (3.34) в виде

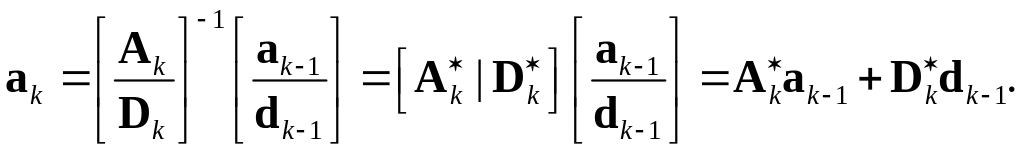(3.36)

Уравнение (3.36) дает практическую формулу для получения из и применяем к и к и складываем результаты. Сравнение с (3.32) показывает, что верно следующее:

Фактически можно напрямую доказать истинность следую­щего соотношения:

(3.37)

где это единичная матрица Выполняется также следующее соотношение:

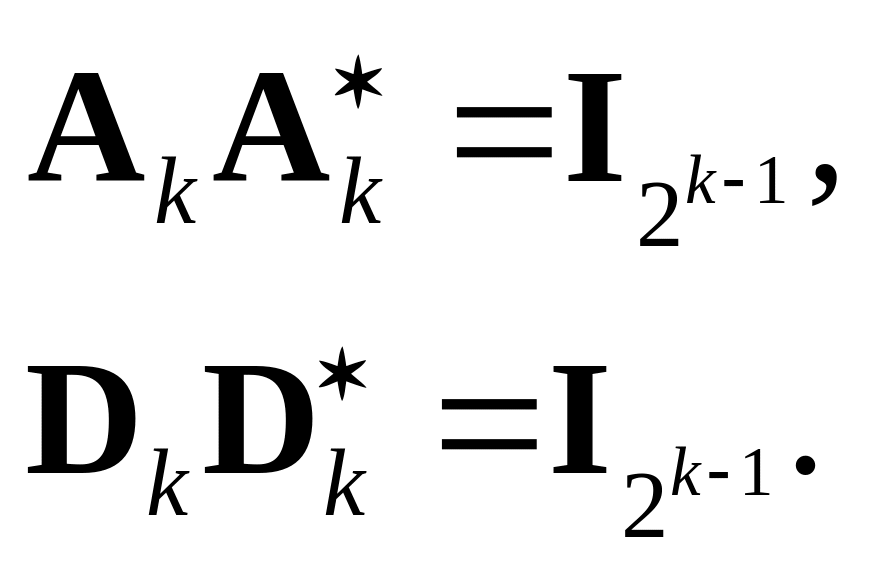(3.38)

Соотношения, ана­логичные (3.37) и (3.38), используются при расчете низкочас­тотных и высокочастотных фильтров.

41