3.2 Масштабирующие функции и вейвлет-функиии

Предположим, что мы рассматриваем наше изображение как функцию на единичном интервале:

(3.6)

где каждое  это характеристическая функция (character­istic function) на интервале , т.е.

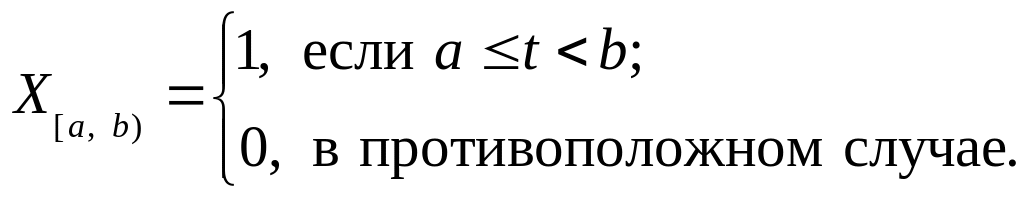
На рис. 3.1 показано, как может выглядеть график такой кусочно-постоянной функции для некоторых, произвольно выбранных, значений Заметим, что если бы мы использовали для аппроксимации непрерывной функции, то для лучшей аппроксимации стоило бы взять больше характеристических функций, определённых на меньших ин­тервалах. Таким образом, чтобы получить лучшую аппроксимацию, нужно использовать лучшее разрешение.

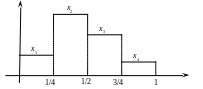
Рисунок 3.1  Функция заданная уравнением (3.6)

Заметим, что это всего лишь сдвиг а именно

Аналогично, это сдвиги . Кроме того,  это масштабирование характеристической функции определённой на единичном интервале, а именно

Таким образом, все характеристические функции в уравне­нии (3.6) могут быть записаны как масштабированные и сдвинутые версии одной единственной функции Введём обозначение

(3.7)

и определим

(3.8)

Тогда

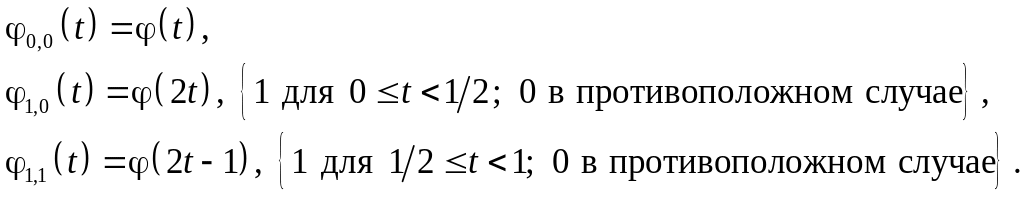
На рис. 3.2 а) и b) показаны некоторые из этих функций. Заметим, что и это масштабированные и сдвинутые версии . Мы назовём масштабирующей функцией. Функ­ция , определённая равенством (3.6), теперь может быть выражена с помощью этих новых функций как:

(3.9)

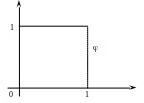
Рисунок 3.2  а) Масштабирующая функция

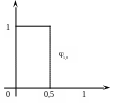
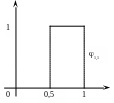
Рисунок 3.2  b) и это масштабированные и сдвинутые версии

Интервал, на котором функция не равна нулю (и, следова­тельно, равна 1) называется носителем (support) этой функ­ции. Заметим, что величина носителя функции уменьша­ется, когда увеличивается. Фактически величина носителя составляет половину величины носителя . Таким об­разом, масштаб или разрешение определяются значением в . Если мы хотим увеличить разрешение, то используем большее значение .

(В лекции 3  обозначает сдвиг, а  обозначает масштаб).

Предположим, что нам нужно проделать процедуру, подоб­ную той, что мы делали в предыдущем разделе. То есть мы хотим представить функцию , заданную уравнением (3.9), с помощью операций усреднения и вычисления раз­ности. Усреднение равнозначно уменьшению разрешения, поэтому мы можем выполнить его, взяв с меньшим значением . Это эквивалентно представлению через и . Коэффициент при в этом представлении  это задан­ный уравнением (3.1), и, таким образом, этот коэффициент является средним значением первых двух коэффициентов . Аналогично, коэффициент при  это и в результате мы получим следующую функцию:

. (3.10)

Очевидно, однако, что не эквивалентна функции . Напри­мер,

тогда как

что, в общем случае, не одно и то же (за исключением вари­анта, когда . При получении из мы использовали только усреднение, поэтому, вероятно, мы потеряли бы информацию, если бы наша исходная функция не содержала очень мало информации с самого начала. В процедуре, опи­санной в предыдущем разделе, отсутствует концепция опре­деления деталей с помощью некоторой операции вычисления разностей. Нам требуется функция, позволяющая выразить разность.

Функция, которую мы ищем, называется вейвлет-функцией. Для данного примера базисная вейвлет-функция (basic wave­let function) задаётся следующим образом:

(3.11)

На рис. 3.3 представлен график вейвлет-функции .

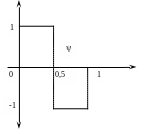
Рисунок 3.3  Базисная вейвлет-функция

Аналогично тому, как мы делали это для масштабирующей функции сейчас введём масштабированный и сдви­нутый вариант . Определим следующим образом:

Тогда, например,

На рис. 3.4 представлены графики и .

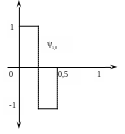
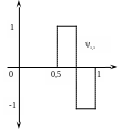
Рисунок 3.4  Функции и представляют собой сжатые и сдвинутые версии базисного вейвлета

Давайте ещё раз рассмотрим задачу выражения функции через средние значения и разности, или, пользуясь нашей но­вой терминологией, через функции масштабирования и вейвлеты. Так как наше конечное разрешение имеет место на ин­тервалах длиной ¼, то мы можем рассмотреть на каж­дом из интервалов [0,¼), ..., [¾,1), чтобы увидеть, где она становится неравной исходной функции . На интервале [0, ¼) разность равна:

На интервале [¼, ½) разность равна:

Таким образом, для , принадлежащего интервалу [0, ½), мы можем записать:

Аналогичный анализ на интервалах [½, ½, ¾) и [¾, 1) пока­зывает, что

для , принадлежащего интервалу [½, 1). Объединив эти ре­зультаты, мы получим новое представление для на всем ин­тервале [0, 1):

(3.12)

Теперь у нас есть представление в виде суммы функций, определённых как средние значения на интервалах длиной ½, и некоторых детализирующих функций, которые нужны нам, чтобы компенсировать разницу с исходным изображением.

Аналогично тому, что мы делали в предыдущем разделе, мы определим теперь среднее значение на всем интервале , заменив первые два слагаемых в (3.12) на а вторые два слагаемых оставив без изменений:

На [0,¼) разность между и составит:

а на [¼, ½) мы получим

Аналогично, на [½, 1) следовательно, на всем интервале мы можем записать как:

(3.13)

Уравнение (3.13)  это аналог последовательности (3.5), но для функций.