Лекции для студентов кафедры ИУ-6 Начальный курс по теории вейвлетов

МГТУ им. Н.Э. Баумана (введение и три лекции)

Начальный курс по теории вейвлетов Введение

Проблема единообразного (в смысле применяемого аппарата) и достаточно простого (в смысле реализации) представления сложных функций всегда представляла интерес для исследователей (математиков в первую очередь). В прошлом столетии этой проблемой вплотную занялись и представители прикладных наук, в частности, таких как связь, радиотехника и средства телекоммуникаций. Можно отметить такие крупные вехи на пути решения этой проблемы, как разложение произвольных (с определёнными ограничениями) функций в ряд Тейлора, полиномиальную и рациональную аппроксимации и, наконец, представление функций и сигналов рядами Фурье.

Сигналы могут быть представлены в виде сумм ортогональных составляющих бесчисленным количеством способов, и поскольку каждый раз система ортогональных функций, применяемая для разложения, бывает известна, то сигналы полностью определяются наборами весовых чисел для этих функций. Такие наборы чисел и есть спектры сигналов. Спектр  это единственно возможная форма аналитического выражения сигналов в рамках линейной теории, и весь вопрос сводится лишь к выбору наиболее подходящей базисной системы функций, удобной для решения той или иной практической задачи.

Из всех возможных спектральных форм представления сигналов наибольшее распространение получили представления в виде колебания и в виде спектра по синусам и косинусам. Эти представления лежат в основе классического спектрального анализа.

С математической точки зрения синусоидальные функции имеют также важные преимущества перед другими системами ортогональных функций. Синусоидальная функция симметрична относительно времени и частоты: повышение частоты колебаний равносильно сжатию функции по времени в такое же количество раз. Многие и наиболее важные системы ортогональных функций порождены дифференциальными уравнениями второго порядка общего вида. И среди этих функций синусоидальные функции являются простейшими. Они соответствуют тому частному, широко распространённому виду систем, для которых коэффициенты описывающего их уравнения постоянны.

Наконец, синусоидальные функции с помощью формулы Эйлера выражаются через комплексные экспоненциальные функции, замечательной особенностью которых является их мультипликативность (при перемножении функций их аргументы суммируются). Именно благодаря мультипликативности этих функций оказалось возможным введение операторного метода, введение понятия коэффициента передачи линейной цепи и др.

Начало решению задачи разложения периодических сигналов в ряд по синусоидальным функциям было положено в XVIII веке Эйлером и Лагранжем. Эта теория приобрела законченную форму в работах Фурье (1807-1822 гг.). Литература, посвящённая спектральному анализу, огромна. Многим крупным математикам удалось внести серьёзный вклад в развитие спектральной теории. Выдающаяся роль в деле развития классических спектральных представлений применительно к задачам радиотехники и автоматики принадлежит Л.И. Мандельштаму, В.А. Котельникову, Г.С. Горелику, С.М. Рытову, Д. Габору, А.А. Харкевичу, Ф.М. Вудворду, Я.3. Цыпкину и др.

Вскоре, после того как был разработан способ разложения функций по синусам и косинусам, было установлено, что эти же функции можно разложить и по другим ортогональным базисным системам, и тем самым достигалось обобщение понятия ряда Фурье. В дальнейшем было показано, что в качестве базисных систем функций могут быть использованы ортогональные многочлены различного типа, собственные функции дифференциальных уравнений чётного порядка, системы «прямоугольных» функций Хаара, Уолша и др.

Разработка различных теоретических и практических аспектов даже классической спектральной теории продолжается до наших дней и вряд ли может считаться полностью завершённой. Тем более это нельзя утверждать в отношении обобщённой спектральной теории. Многие принципиальные вопросы этой теории ещё не разрешены, но ещё больше вопросов, уже решённых математиками, до сих пор не интерпретированы таким образом, чтобы они смогли стать достоянием широких кругов специалистов в области радиотехники и автоматики и могли использоваться в практических целях.

Отсутствие обобщённой спектральной теории, приспособленной к задачам передачи и обработки сигналов, которая бы раскрывала основные закономерности спектрального анализа, общие для всех систем базисных функций, и создавала возможность синтеза наиболее выгодных базисных систем,  это одна из причин, затрудняющих в настоящее время практическое применение различных способов спектрального представления сигналов.

Но имеется и другая, не менее важная причина, тормозившая применение обобщённой спектральной теории. Она связана с тем, что новые базисные функции в отличие от синусоидальных трудно генерировать и обрабатывать с помощью обычных аналоговых схем с постоянными параметрами, которые были единственно возможными на протяжении многих лет.

В последнее время в этой области положение резко изменилось. Новая полупроводниковая электроника, а затем и микроэлектроника дали возможность реализовать большое разнообразие схем с переменными параметрами. Ещё большее значение имеют новые возможности обработки сигналов в любой базисной системе, которые открылись благодаря применению ЦВМ. Тем самым в настоящее время открыт путь для широкого практического использования новых спектральных представлений сигналов, и это обстоятельство делает ещё более актуальной задачу дальнейшего развития обобщённой спектральной теории.

Чтобы ещё более подчеркнуть целесообразность и своевременность развития такой теории, имеет смысл хотя бы кратко перечислить основные направления, по которым можно ожидать в будущем особенно большого эффекта.

1 Если источник, образующий сигналы, и приёмник, на который они поступают, имеют конкретные физические ограничения, то можно выбрать такую базисную систему функций для разложения сигналов, согласованную со свойствами источника и приёмника, при которой для передачи сигналов потребуется минимальное количество данных. Другими словами, выбрав соответствующую систему разложения, можно уменьшить избыточность передаваемой информации.

Не исключено, что удастся найти такую систему функций для разложения, при которой для передачи речевых сигналов потребуется весьма узкая полоса обобщённых частот. Тогда, применив обобщённую теорему Котельникова, можно будет передавать речь с помощью минимального числа отсчётов.

Разумеется, возможны и такие практические задачи, когда необходимо ввести некоторую избыточность представления сигналов (например, в целях борьбы с помехами в канале связи). Эти задачи также могут решаться путём выбора соответствующей базисной системы.

2 Обычно на принимаемый сигнал в линии связи накладываются шумы и помехи. Выбрав соответствующую базисную систему функций, учитывающую особенности сигналов и шумов, можно попытаться уменьшить или вообще устранить перекрытие их спектров (т.н. элайзинг). Тем самым будут созданы условия для наилучшей фильтрации сигнала.

Новый подход может оказаться полезным даже в том случае, когда шум является «белым» и ставится только задача обнаружения сигнала. Известно, что наилучший результат в этом случае будет достигнут, когда применяется оптимальный фильтр, согласованный с сигналом. Если такой фильтр удастся реализовать, то он даст на выходе максимально возможное отношение пикового значения сигнала к среднеквадратическому значению шума. Однако в случае сложных сигналов его практическая реализация с помощью устройств с постоянными параметрами, основанных на классическом гармоническом анализе, может оказаться затруднительной.

В этих случаях значительно лучший результат может быть получен с помощью линейных фильтров с переменными параметрами, каждый из которых описывается в наиболее простом для него собственном базисе. Функции из этого базиса обладают тем свойством, что, проходя через линейную цепь, они не изменяют своей формы. Тем самым расширяются возможности реализации согласованных фильтров.

3 Применение новых базисных систем для разложения сигналов может существенно облегчить анализ и синтез цепей с переменными параметрами. По-видимому, в ряде случаев выбором соответствующего базиса можно будет свести такие задачи к хорошо проработанным задачам классического анализа для цепей с постоянными параметрами.

4 В настоящее время исследуется обширная область цифровой обработки сиг­налов, получившая за рубежом громадное развитие. Это методы и средства цифровой обработки многомерных сигналов  неподвижных изображений, видео, меняющихся во времени томографических, сейсмических и многих других сигналов. В последнее время с этой целью все чаще стали использоваться неразделимые опера­торы, которые являются операторами наиболее общего вида. Сейчас можно говорить о новом научно-техническом направлении в области информационно-телекоммуникационных технологий и обработ­ки сигналов. Это разработка теории многомерных систем и методов обра­ботки многомерных сигналов, развитие которых стимулируется важными практическими задачами. Многомерные сигналы описываются функция­ми нескольких переменных и могут обрабатываться только многомерны­ми системами, т.е. системами, описываемыми функциями и уравнениями многих переменных. Интенсивное развитие данного направления основано на теории одномерных и многомерных сигналов и систем, а также на таких разделах математики, как теория функций многих переменных, компьютерная алгебра, теория вейвлет-преобразования, функциональный анализ, аппроксимации и др.

Этот перечень можно было бы продолжить, включив в него много других направлений.

Итак, для решения различных практических задач необходимо искать адекватные этим задачам спектральные системы. В связи с этим возникает проблема синтеза базисной системы функций.

Таким образом, известные методы представления сигналов и функций постоянно наталкивались на принципиальные теоретические ограничения, не позволяющие всерьёз говорить о принципиальном решении проблемы единообразного представления функций и сигналов (особенно нестационарных) методами, созданными на основе средств преобразований Фурье. Так продолжалось до открытия вейвлетов, которые, похоже, наконец, решили эту сложнейшую и актуальную научную проблему. Основой этого решения стала разработка принципиально нового базиса и класса функций, которые используются для декомпозиции и реконструкции функций и сигналов  в том числе нестационарных. Соответственно был создан и новый аппарат представления функций и сигналов, а уже совсем недавно и необходимые инструментальные и программные средства для его реализации.

В последние десятилетия в мире возникло и оформилось новое научное направление, связанное с так называемым вейвлет-преобразованием. Слово «wavelet», являющееся переводом французского «ondelelte», означает небольшие волны, следующие друг за другом. Можно без преувеличения сказать, что вейвлеты произвели революцию в области теории и практики обработки нестационарных сигналов. В настоящее время вейвлеты широко применяются для распознавания образов; при обработке и синтезе различных сигналов, например речевых, медицинских; для изучения свойств турбулентных полей и во многих других случаях.

Вейвлеты были введены сравнительно недавно, в конце 1980-х. Вейвлет-анализ может быть охарактеризован как альтернатива классическому взвешенному анализу Фурье. Строительными блоками взвешенного анализа Фурье являются синусы и косинусы (волны), умноженные на скользящее окно. Они обычно называются частотно-временными атомами. В вейвлет-анализе окно изначально являет­ся осциллирующим и называется «материнским вейвлетом». Вместо умножения на синусы и косинусы этот вейвлет произвольно сдвига­ется и растягивается по временной оси. Таким образом, генерирую­щий (или материнский) вейвлет образует другие вейвлеты, которые являются строительными блоками вейвлет-анализа. Эти растяжения соответствуют различным степеням увеличения, а вейвлеты выпол­няют роль масштабно-временных атомов вейвлет-анализа.

Анализ Фурье, взвешенный анализ Фурье и вейвлет-анализ осно­ваны на одной и той же концепции. Во всех трёх случаях, анализ функции заключается в вычислении всех корреляций между задан­ной функцией и частотно-временными или масштабно-временными атомами. Синтез производится в предположении, что эти атомы образуют ортонормированный базис.

Среди специалистов по численному анализу и обработке изобра­жений принято считать, что величина, обратная масштабу, являет­ся частотой: малые масштабы соответствуют низким частотам, а большие масштабы соответствуют высоким частотам. Кроме того, значительно различающиеся масштабы должны давать независимую (т.е. неизбыточную) информацию о сигнале.

Теория вейвлетов является мощной альтернативой анализу Фурье и даёт бо­лее гибкую технику обработки сигналов. Одно из основных преимуществ вейвлет-анализа заключается в том, что он позволяет заметить хорошо локализован­ные изменения сигнала, тогда как анализ Фурье этого не даёт в коэффициентах Фурье отражается поведение сигнала за все время его существования. Разработана глубокая и красивая математическая теория вейвлетов.

Вейвлеты по существу являются новыми математическими понятиями и объектами, применение которых может теоретически строго приблизить любую функцию или любой сигнал. Поэтому они весьма перспективны в решении многих математических задач приближения (интерполяции, аппроксимации, регрессии и т.д.) функций, сигналов и изображений. Вейвлет-обработка сигналов обеспечивает возможность весьма эффективного сжатия сигналов и их восстановления с малыми потерями информации, а также решение задач фильтрации сигналов. Таким образом, вейвлеты существенно пополняют традиционные средства обработки сигналов и изображений.

Но особенно важна принципиальная возможность вейвлетов представлять нестационарные сигналы, например, состоящие из разных компонент, действующих в разные промежутки времени, модулированные сигналы и т.д. Такие сигналы в наше время находят куда более широкое применение, чем стационарные или квазистационарные (искусственно сводящиеся к стационарным) сигналы, а также процессы и системы их порождающие. Как известно, ряды и преобразования Фурье в классическом виде непригодны для представления нестационарных сигналов, процессов и систем. Поэтому возможность их представления вейвлетами трудно переоценить.

Вейвлеты (wavelets)  это обобщённое название особых функций, имеющих вид коротких волновых пакетов с нулевым интегральным значением и с той или иной, подчас очень сложной, формой, локализованных по оси независимой переменной или и способных к сдвигу по ней и масштабированию (сжатию/растяжению).

Вейвлеты создаются с помощью специальных базовых функций  прототипов, задающих их вид и свойства и удовлетворяющих целому ряду специфических условий. Набор вейвлетов, в их временном или в частотном представлении, может приближать сложный сигнал или изображение, причём идеально точно или с некоторой погрешностью. Таким образом, вейвлеты  это новый математический и практический аппарат представления и обработки произвольных функций, сигналов и изображений, о чем и говорилось выше.

По своей значимости роль вейвлетов можно сравнить разве что с выдающейся ролью рядов Фурье и преобразований Фурье. Но вейвлеты имеют явные преимущества перед рядами Фурье как в общем и точном представлении функций, так и их разнообразных локальных особенностях. Они представлены намного более разнообразным набором типов, чем единственная синусоидальная функция в рядах Фурье. Это разнообразие вейвлетов с одной стороны резко расширяет круг решаемых с их помощью прикладных задач, а с другой стороны делает такое решение творческим, а вовсе не рутинным процессом.

В области обработки изображений вейвлеты дают новейшие и весьма эффективные способы их обработки, например, декомпозиции, реставрации и идентификации сигналов и изображений, удаления из них шума, сжатия файлов, хранящих данные и изображения, и т.д. и т.п. Обширный набор базовых функций вейвлетов и множество их типов позволяют легко адаптировать их к решению тех или иных конкретных и общих задач практики.

Особо большое развитие получила практика применения вейвлетов для решения задач сжатия и обработки изображений, являющихся нестационарными по своей природе. В этой области применение вейвлет-преобразования позволило достичь одновременного снижения сложности и повышения эффективности кодеров. В настоящее время уже находятся в разработке международные стандарты по сжатию неподвижных изображений и видео  JPEG2000 и MPEG-4. Ядром этих стандартов будет вейвлет-преобразование.

Теория и практика вейвлет-преобразования находится на стыке различных наук: математики, физики и т.д.

И.И. Добеши и С. Малла показали, что практическое выполнение вейвлет-преобразования осуществляется посредством двухполосного банка фильтров анализа-синтеза, известного ранее в теории субполосного кодирования. Эта теория может быть описана в терминах вейвлетов. Главное различие между этими двумя направлениями заключается в критериях построения фильтров, как это будет показано далее.

Некоторые идеи теории вейвлетов частично были разработаны уже очень давно. Например, А. Хаар опубликовал в 1910 г. полную ортонормальную систему базисных функций с локальной областью определения. Эти функции называются теперь вейвлетами Хаара.

Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Эти функции могут быть симметричными, асимметричными и несимметричными. Различают вейвлеты с компактной областью определения и не имеющие таковой. Некоторые функции имеют аналитическое выражение, другие - быстрый алгоритм вычисления связанного с ними вейвлет-преобразования. Вейвлеты различаются также степенью гладкости. Для практики желательно было бы иметь ортогональные симметричные (асимметричные) вейвлеты. К сожалению, доказана теорема о том, что такими вейвлетами являются лишь вейвлеты Хаара. Функции Хаара не обладают достаточной гладкостью и не подходят для большинства приложений. Поэтому для кодирования изображений обычно используют биортогонатьные вейвлеты.

Российские математики вейвлеты называют всплесками. Теория всплесков лежит на пересечении чистой математики, вы­числительной математики, а также проблематики аудио и графической обработки сигналов, сжатия и передачи информации.

Слово всплеск – эквивалент английского «wavelet», которое в свою очередь является переводом французского «ondellete», первоначально введённого А. Гроссманом, Й. Морле. При внедрении терминологии в русскоязычную литературу возникали многочисленные варианты, среди которых в качестве «wavelets» использовались слова: онделлеты, вейвлеты, вэйвлеты, волнушки, волночки. В конечном итоге мате­матики выбрали предложенный К.И. Осколковым термин «всплеск», который не является точным переводом слова «wavelet», но зато хо­рошо отражает суть происходящего. Под системами всплесков обыч­но понимают сжатия и сдвиги одной функции, образующие систему представления в каком-либо смысле (например, ортогональный базис в . B некоторых ситуациях системы всплесков состоят из сдвигов и сжатий нескольких функций или целой последовательности. Поня­тие «всплеск» как таковое не вводится, конкретный смысл придаётся таким словосочетаниям, как «всплеск-функция», «последовательность всплеск-функций», «пространство всплесков» и т.п.

Ради полноты, необходимо отметить, что изучение атомарных функций началось в 1971г., когда была по­строена функция (термин «атомарная функция» появился в 1975 г. в работе В.Л. Рвачёва и В.А. Рвачёва.

История возникновения функции

следующая. В 1967 г. В.Л. Рвачёвым была поставлена задача. Если – финитная дифференцируемая функция, имеющая один участок возрастания и один участок убывания («горб»), то её производная со­стоит из «горба» и «ямы». Существует ли функция, , у которой «горб» и «яма» производной подобны горбу самой функции? На языке уравнений это означает: существует ли финитное решение уравнения , в котором (для определённости считаем) что носитель – отрезок

Таким образом, вейвлеты могут с успехом приме­няться для решения различных, проблем. Однако они ещё недостаточно широко известны кругу исследовате­лей, занимающихся анализом экспериментальных и на­турных данных. В настоящей работе сделана попытка по возможности наглядно и просто изложить сведения из теории вейвлетов, необходимые при практическом при­менении вейвлет-преобразования для анализа сигналов различной природы.

Сегодня мы сталкиваемся с целым рядом нерешённых проблем:

– в системах сжатия почти не используется вейвлет-преобразование (кроме JPEG-2000);

– все известные стандарты сжатия являются разделимыми (покоор­динатная обработка);

– отсутствуют стандарты сжатия реальных трёхмерных, четырёх­мерных ... сигналов, а также мультиспектральных сигналов дистан­ционного зондирования Земли;

– для создания систем визуализации многомерных сигналов (в трёх­мерном телевидении, при обработке фотореалистичных световых полей) нужны эффективные системы сжатия многомерных сигна­лов с низкой вычислительной сложностью.

Задачи цифровой обработки сигналов обычно требуется решать с большой скоростью (часто в реальном времени) и в необычных условиях (на борту корабля, в поле), для чего универсальные ЦВМ непригодны. Поэтому много усилий прилагается для создания спецпроцессоров.

В течение последних лет резко возрос интерес к решению задач ана­лиза, синтеза, обработки, кодирования, сжатия многомерных (ММ или M-D  multi-dimensional) сигналов для их передачи, хранения, архи­вирования, защиты от несанкционированного доступа, восстановления в системах связи (проводных и беспроводных) при наличии ограничений (на скорость передачи, на полосу пропускания, на динамический диапазон и т.д.). Это объясняется громадным ростом таких областей приложе­ния, как мультимедиа технологии и телекоммуникации, осуществляющих обработку (включая сжатие) неподвижных изображений (2-D сигналы), видеосигналов (3-D сигналы) и меняющихся во времени томографических снимков (4-D сигналы).

ММ цифровые фильтры (в том числе адаптивные) предпочтительны также при восстановлении изображений, так как они позволяют эф­фективно использовать корреляцию между соседними пикселями изобра­жения, отслеживать пространственные изменения в распределении ММ сигнала и использовать иную априорную информацию о ММ сигналах.

Теория обработки ММ сигналов разделяет детерминированные и ста­тистические подходы к моделированию, анализу и синтезу простран­ственно-временных дискретных и непрерывных систем. Сейчас очевидно, что тема ММ систем непосредственно связана с теоретическими и при­кладными проблемами, которые возникают из-за непрерывно растущих требований в области приложений. Известно, что проблема обработки сигналов в сущности многомерная, но обычно решается после свёртыва­ния на одно из нескольких измерений.

В то время как большинство разработок было сконцентрировано на одномерных сигналах и ММ случай был реализован лишь через тензор­ное произведение, некоторые исследователи сосредоточили свои усилия на «истинном» ММ случае. Под «истинным» ММ случаем нужно понимать то, что допускается: и неразделимое осуществление дискретизации, и не­разделимая фильтрация. Хотя «истинный» ММ подход может иметь ряд недостатков (более высокую вычислительную сложность, потенциальные проблемы устойчивости в случае ММ рекурсивной фильтрации), он даёт некоторые неоспоримые преимущества. Например, использование нераз­делимых фильтров ведёт к большему количеству степеней свободы и при этом, следовательно, можно синтезировать лучшие фильтры. Кроме то­го, неразделимое осуществление дискретизации открывает возможность создания схем, лучше приспособленных к визуальной системе человека.

Рассмотрим сначала основные типы многомерных сигналов:

– неподвижные изображения (две пространственные координаты) – 2-D сигналы;

– видеосигналы (две пространственные координаты, время) – 2,5-D сигналы, томографические (три пространственные координаты) – 3-D сигналы;

– зависящий от времени томографический сигнал (три простран­ственные координаты, время) или видеосигнал, снимаемый несколь­кими камерами (две пространственные координаты, время и номер камеры)  4-D сигналы;

– световые поля (три пространственные координаты для позиции взгляда и две для направления взгляда) – 5-D сигналы;

– пленоптическая функция, включающая в себя всю доступную ин­формацию о световом потоке (три пространственные координаты, два угла зрения, цвет (длина волны) и время) – 7-D сигналы.

Важно понять разницу между разделимыми и неразделимыми сигна­лами. Для этого можно рассмотреть описание сигналов, фильтров и т.д. в -области. Для разделимого сигнала соответствующая частотная или временная характеристика факторизуема в произведение одномерных ха­рактеристик, в то время как для неразделимого сигнала такое разложение на множители выполнить невозможно:

– разделимый сигнал/фильтр

– неразделимый (несепарабельный) сигнал/фильтр

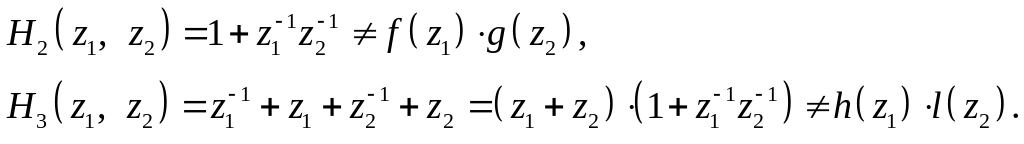
Разработки в области цифровой обработки сигналов, проводимые в промышленно развитых странах, уже привели к созданию ряда стан­дартов (из последних это упомянутый JPEG-2000 для сжатия неподвиж­ных изображений и разрабатываемые стандарты сжатия видео Н.265, MPEG-7 и MPEG-21) и производству специализированных СБИС и сигнальных процессоров. Однако задача создания методов и средств соответствующего аппаратного комплекса для многоскоростных систем, удовлетворяющего заданным требованиям (по коэффициенту сжатия, по качеству восстановленного после сжатия сигнала, по быстродействию и т.д.), разработанного и реализованного в наиболее общем -- нераз­делимом виде и пригодного для широкого внедрения, ещё не решена.

Существует целый ряд приложений, в которых цифровая обработка ММ сигналов играет ключевую роль. Среди них можно назвать следующие:

 системы сжатия ММ сигналов (многоскоростные системы, транс­мультиплексоры) ;

 удаление шумов;

 системы обработки мультиспектральных сигналов дистанционного зондирования Земли;

 системы трёхмерной визуализации (трёхмерное телевидение 3D-TV, обработка световых и акустических полей).

Эффективным способом преобразования ММ сигналов является при­менение ММ многоскоростных систем. С их помощью сигнал может быть представлен в виде, более удобном для решения многих приклад­ных задач, таких как сжатие (с потерями или без потерь), удаление шумов, распознавание образов и др. Многоскоростные системы состоят из цифровых фильтров и устройств изменения плотности отсчетов в про­странственно-временной области, поэтому обработка сигнала в различ­ных частях системы происходит с разной скоростью. Применение таких систем позволяет строить схемы кратномасштабного анализа на основе вейвлетов. Использование вейвлет-преобразования позволило одновремен­но снизить сложность и повысить эффективность кодеков.

Цифровые многоскоростные наборы, или, как их чаще называют, бан­ки фильтров (БФ) впервые описаны в [139], где он использовались для сжатия речи. В дальнейшем они стали применяться шире, главным образом, для кодирования подполос речи, статических изображений и ви­део. Основы теории исходили из того, чтобы отсутствовали наложение и искажение сигналов. Речь шла о синтезе систем, достигаю­щих точного восстановления сигнала в одном или нескольких измерениях, от двухканальных ортогональных банков до многоканальных систем. Для выполнения этих требований все усилия были сконцентрированы на фильтрах, имеющих дробно-рациональные функции преобразования, т. е. на линейных инвариантных к сдвигу системах.

Независимо от этих работ в прикладной математике была разрабо­тана теория вейвлетов. С работами Добеши, Малла и Мейера стало ясно, что банки фильтров и вейвлеты связаны неразрывно. Банки филь­тров вычисляют эквивалент дискретного вейвлет-преобразования, и при известных условиях они могут использоваться для получения непрерыв­ных вейвлет-базисов. Практика применения вейвлетов для решения задач сжатия и обработки изображений и видео, являющихся нестационар­ными по своей природе, получила большое развитие. В этой области применение вейвлет-преобразования позволило достичь одновременного снижения сложности и повышения эффективности кодеков. В настоящее время разработаны международные стандарты по сжатию неподвиж­ных изображений и видеосигналов – JPEG-2000, H.264/AVC, WMP10 и MPEG-4. Стандарт JPEG-2000 является единственным стандартом, основанным на вейвлет-преобразовании. Тем самым задача синтеза ММ многоскоростных систем и схем вейвлетного кратномасштабного анали­за, построенных на их основе, является исключительно важной, в том числе для будущих стандартов сжатия ММ сигналов.

Многоскоростные системы состоят из двух наборов (банков) фильтров – банка анализа и банка синтеза. В зависимости от того, в каком порядке они соединены, можно получить различные устройства. В случае, если на вход банка анализа подаётся сигнал, который раскладывается на подполосовые составляющие и далее восстанавливается обратно в банке синтеза, такая система называется банком фильтров анализа/синтеза (устоявшегося названия нет, поэтому это устройство будет называться просто «многоскоростной системой»). Если поменять порядок следования банка анализа и банка синтеза, в этом случае набор сигналов подаётся на вход банка синте­за, с выхода которого комбинированный сигнал подаётся на вход банка анализа, производящего его разложение на составляющие. Такая систе­ма называется банком фильтров синтеза/анализа, или (в данном случае имеется устоявшееся название) трансмультиплексором. Очень важно то, что обе системы описываются по сути одними и теми же типами уравнений.

Будем рассматривать линейные преобразования сигналов конечного раз­мера, которые могут быть выражены в терминах свёртки с КИХ-фильтрами. На рис. I показана система, осуществляющая такое преобразование при помощи банков фильтров анализа-синтеза.

Обозначения на рисунке являются стандартными для цифровой обработ­ки сигналов. означает операцию круговой свёртки входного сигнала длиной с импульсной характеристикой КИХ-фильтра и Фурье-преобразованис результата:

(1.1)

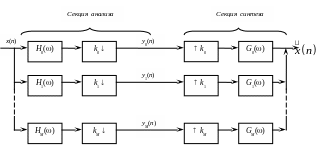
Рисунок I  Банк фильтров анализа-синтеза

Естественным образом предполагается, что длина фильтра меньше разме­ра изображения. Блоки означают децимацию в раз, блоки  ин­терполяцию в раз. Напомним, что децимация означает оставление лишь каждого отсчёта, интерполяция означает вставку нулей между этими отсчётами. Предполагается, что  целые числа и делят .

Будем называть такую систему системой А-С. Секция анализа системы А-С выполняет линейное преобразование над входным сигналом дли­ной . В результате получается последовательностей длиной . Операции, выполняемые секцией синтеза, являются обратными операциям секции анализа. В результате получается сигнал . Точно так же строится система А-С и для многомерного сигнала.

Таким образом, коэффициенты преобразования вычисляются через свёрт­ку. Интуитивно понятно, что это хорошо, так как различные участки сигнала будут обрабатываться одинаковым образом. Далее, формулирование про­блемы в частотной области позволяет легко разделить ошибку реконструк­ции на две части: элайзинговую составляющую и состав­ляющую, инвариантную к сдвигу. Для этого запишем выходной сигнал схе­мы анализа в частотной области:

(1.2)

Тогда выходной сигнал схемы А-С

(1.3)

с учётом эффекта интерполяции и децимации в частотной области. Объеди­няя выражения (1.2) и (1.3), получаем

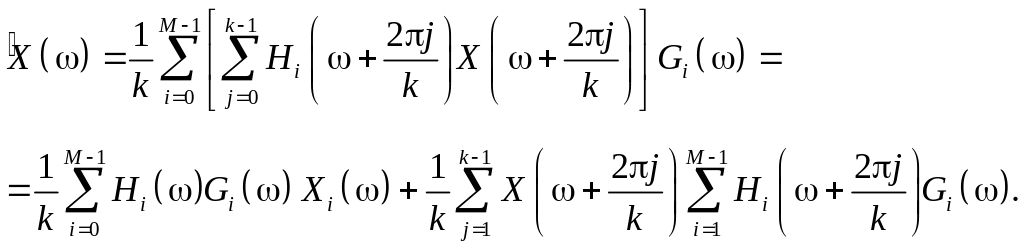(1.4)

Здесь первое слагаемое соответствует отклику линейной времянезависимой системе, а второе соответствует элайзингу системы.

История развития полиномиальных методов. Синтез многомерных цифровых фильтров требует развития теории мно­гомерных полиномов, потому что именно полиномы формируют пере­даточные функции цифровых фильтров в комплексной -области и ча­стотной области. В пространственной области фильтры характеризуются многомерными импульсными характеристиками. Следует подчеркнуть, что переход от одномерного к многомерному случаю является не только количественным, но и, в первую очередь, качественным. Многие пробле­мы, с которыми приходится сталкиваться при обработке многомерных сигналов, просто не существуют при обработке одномерных сигналов. То же относится и к теории систем. Развитие теории систем для обработ­ки сигналов тесно связано с развитием теории полиномов. С этой точки зрения можно выделить несколько этапов.

Первые исследования были связаны с изучением полиномов одной переменной (одномерный случай). Следующим этапом было изучение од­номерных MIMO систем с несколькими входами и выходами, и он связан с изучением матриц, элементами которых служат многочлены. В одно­мерном случае анализ таких систем связан с исследованием матричных многочленов от одной переменной. Важные обобщающие результаты для систем со многими входами и многими выходами (для одномерного слу­чая) были получены в конце 80-х – начале 90-х годов.

Хронологически в третьей группе оказались задачи, связанные с мно­гомерными многочленами. Возникнув в начале 60-х годов, они к настоя­щему времени приобрели особое значение в связи с необходимостью раз­вивать, в первую очередь, технику цифровой фильтрации в ММ случае. При переходе от многочленов, зависящих от одной переменной, к много­членам, зависящим от нескольких переменных, резко возрастают матема­тические трудности. Это объясняется тем, что, в отличие от одномерного случая, многочлен от многих переменных раскладывается на неприводи­мые множители, каждый из которых может зависеть от нескольких, а не от одной переменной, в то время как в случае с одной переменной неприво­димые множители зависят только от одной переменной (основная теорема алгебры). Ещё одно существенное и важное отличие состоит в том, что ес­ли корни уравнения всегда являются изолированными точками, то для уравнения решениями являются многомерные поверхности или многообразия. Эффективное решение подобных задач связано с так называемой алгебраической теорией разрешимости, построенной Тарским-Зайденбергом и получившей элегантное решение с помощью базисов Грёбнера.

Понятие базисов Грёбнера было впервые предложено Бруно Бухбергером в его диссертации в 1966 г. С тех пор теория получила развитие, а многочисленные применения можно найти и в математике, и во многих технических приложениях. Базисы Грёбнера являются мощ­ным средством, так как они позволяют эффективно проводить различные вычисления с многомерными многочленами. Алгоритм Бухбергера для построения базисов Грёбнера для многомерного полиномиального идеала обобщает и алгоритм Евклида для одномерных многочленов, и алгоритм Гаусса приведения к треугольному виду для линейных систем. Поэтому естественным является применение базисов Грёбнера для задач, требую­щих использования как алгоритма Евклида, так и алгоритма исключения Гаусса. Задачи многомерной фильтрации сигналов как раз относятся к та­кого рода задачам.

Четвертая группа рассмотренных задач связана с изучением матриц, элементами которых служат многочлены с несколькими переменными. Те­ория таких матриц получила существенное развитие в начале 90-х годов. Получены обобщающие результаты, позволяющие разложить некоторые классы многомерных полиномиальных матриц в произведение элементар­ных матриц, достроить матрицы до полного размера при наличии одной (или нескольких) её строк (или столбцов).

С проблемой факторизации многочленов связан важный вопрос об ан­нулирующем множестве, или множестве решений многочленного урав­нения с переменными. Решение может быть только тривиальным либо возможны нетривиальные нули. Вопрос о существова­нии нетривиальных нулей тесно связан с проблемой положительности или неотрицательности многочленов нескольких переменных.

В общем случае передаточная функция многомерного фильтра в про­странстве комплексных переменных является отношением многочленов, т.е. дробно-рациональной функцией (рекурсивный случай). При этом, если числитель и знаменатель такой функции  взаимно простые мно­гочлены (многомерные), то возможен случай, когда их аннулирующие множества (т.е. множества переменных, обращающие многочлен в нуль) пересекаются. Это приводит к появлению особых точек, называемых не­существенными особыми точками второго рода. Нуль одного многочлена, который не является нулём другого, называется несущественной особой точкой первого рода.

Теория идеалов и модулей (проективных и конечно порождённых) над полиномиальными кольцами и кольцами полиномов Лорана используется во многих приложениях. Геометрически такие идеалы и модули соот­ветствуют аффинным и торическим многообразиям и, соответственно, пучкам векторов над ними. Алгебро-геометрические результаты, свя­занные с пучками алгебраических векторов над алгебраическим тором, напрямую оказывают влияние на теорию КИХ банков фильтров, так как конечно порождённые проективные модули над кольцами полиномов Ло­рана представлены именно такими пучками векторов.

Вычислительная сторона этой теории, однако, имеет достаточно ко­роткую историю. Базисы Грёбнера лежат в её основании.

В 1955 г. Ж.П. Серр высказал гипотезу о тривиальности пучков алге­браических векторов над аффинным пространством. В 1976 г. независимо друг от друга А.А. Суслин и Д. Куиллин доказали, что конеч­но порождённые проективные модули над кольцами полиномов свободны. Приведённые ими доказательства были неконструктивными. Алгоритми­ческие доказательства были приведены позже, а также в диссертациях.

Сразу после доказательства гипотезы Серра А. Суслин доказал -ана­лог гипотезы Серра о разложимости унимодулярной полиномиальной матрицы размером (где принадлежат коммутатив­ному нётерову полиномиальному кольцу в произведение элементарных множителей при . При не любая унимодулярная матрица может быть разложена в произведение элементарных множителей (элементарных матриц).

В рамках полиномиального подхода разработаны и исследованы не­сколько основных методик синтеза ММ БФ:

1. Применение полиномов Бернштейна.

2. Применение методики лифтинга, синтез ММ фильтров с дробным (постоянным или переменным) ММ сдвигом.

3. Метод достройки матрицы до полной по заданной её части.

4. Синтез ММ фильтров с чётным размером носителя.