2.1.1 Определение вейвлета

Любая локализованная -функция называется -вейвлетом (или просто вейвлетом), если для неё су­ществует функция (её пара, двойник) такая, что семейства и , построенные согласно (1.9) и (1.17), являются парными базисами функционального про­странства .

Каждый таким образом определённый вейвлет , независимо от того, ортогональный он или нет, позво­ляет любую функцию представить в виде ряда (1.10), коэффициенты которого определяются интеграль­ным вейвлет-преобразованием относительно .

Вейвлет-двойник  единственный и сам является -вейвлетом. Пара симметрична в том смысле, что в свою очередь является двойником для .

Если -вейвлет обладает свойством ортогонально­сти, то , и  ортогональный базис.

Для многих практических целей достаточно, чтобы вейвлет обладал свойством полуортогональности, т.е. чтобы его базис Рисса удовлетворял условию при .

-вейвлет называется неортогональным, если он не является полуортогональным вейвлетом. Однако, будучи -вейвлетом, он имеет двойника, и пара даёт возможность сформировать семейства и , удовлетворяющие условию биортогональности и позволяющие построить полноценные ряд по вейвлетам и реконструкционную формулу.

С необходимостью иметь обратное вейвлет-преобразование (или реконструкционную формулу) связано большинство ограничений, накладываемых на вейвлет.

2.1.2 Другие системы вейвлетов

Рассмотренные вейвлеты Хаара  это только маленький пример из огромного множества систем вейвлетов, используемых в приложениях обработки сиг­налов и изображений. Как уже говорилось, системы вейв­летов Хаара обладают свойством компактности носителя, а также ортогональности. Таким образом, мас­штабирующие функции и вейвлет-функции удовле­творяют равенствам:

(2.1)

Кроме того, эти функции также удовлетворяют равенству

(2.2)

Есть и другие свойства, которые могут быть полезны в сис­темах вейвлетов. Одно из таких свойств  это симметрия, т.е. масштабирующие функции и вейвлет-функции симметричны относительно своих центров. Вейвлеты Хаара удовлетворяют этому свойству, но фактически вейвлеты Хаара  это единственные вейвлеты одновременно и симметричные, и ортогональные, и обладающие компактным носителем.

Поэтому, например, если нам нужны гладкие, симметричные вейвлеты с компактным носителем, мы должны отказаться от ортогональности. Многие из более новых систем вейвлетов, используемых в приложениях, не являются ортогональными в смысле удовлетворения условиям (2.1) и (2.2), но зато удовлетворяют некоторым более слабым свойствам ортого­нальности. Одно такое свойство  это полуортогональность. Полуортогональные системы вейвлетов удовлетворяют равенству (2.2), но не удовлетворяют (2.1).

Другая слабая форма ортогональности это биортогональность. Биортогональность относится к концеп­ции двойственности. Предположим, что это множество неортогональных базисных функций. Мы можем представить функцию в виде линейной комбинации этих ба­зисных функций:

Отсутствие ортогональности делает затруднительным опреде­ление коэффициентов . (Пусть, например,  вейвлет-базис пространства , который не является ортого­нальным. Для , как обычно, найдём коэффициенты:

Если мы хотим восстановить по вычисленным коэффициентам, то не можем надеяться на равенство

поскольку функции не ортонормированы и даже не ортогональны. Дей­ствительно, по формуле

.

Проблема восстановления функции по её коэффициентам может быть решена с использованием двойственного базиса в следующим образом. Рас­смотрим сначала случай конечномерного евклидова пространства . Возьмём базис (не ортогональный) в пространстве . Для любого пусть

Мы хотим восстановить по его коэффициентам . Поскольку базис не ортонормированный, то  это не коэффициенты разложения по базису , поэтому . Попробуем найти другой базис , в котором

Если такой базис существует, то мы должны иметь следующее (берём скаляр­ное произведение с обеих частей последнего равенства):

для любого . Это имеет место только тогда, когда  сим­вол Кронекера. Для его построения мы сначала опреде­ляем двойственный базис линейных функционалов на , т.е. таких функционалов , что

Поскольку наше пространство является евклидовым, то по теореме Рисса каж­дый функционал задаётся как скалярное произведение с некоторым вектором . Полученные векторы и составляют искомый дуальный базис про­странства

Однако существует другой базис такой что

Функции обладают также свойством

Базис называется двойственным базисом, соответствующим . Биортогональные вейвлет-системы состоят из четырёх множеств функций: базиса мас­штабирующих функций , двойственного к нему базиса , базиса вейвлет-функций , двойственного к нему базиса Условие биортогональности требует, чтобы эти множества функций удовлетворяли следующему свойству:

Кроме того, двойственность влечёт за собой

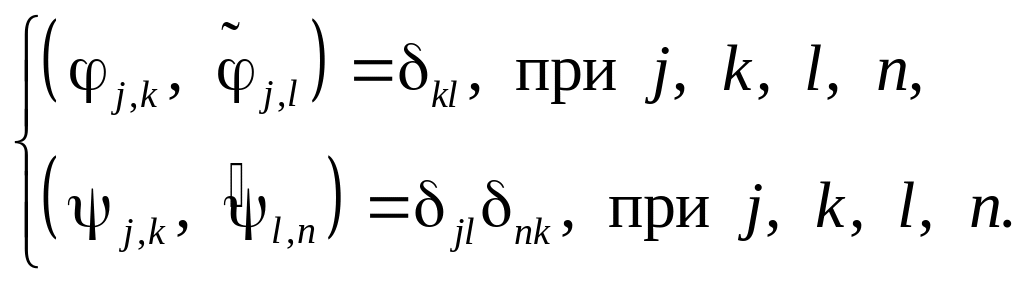
Биортогональные системы вейвлетов стали распространён­ным средством в приложениях по сжатию изображений. (Насчитывается около 5000 биортогональных систем вейвлетов для приложений по сжатию изображений.)