1.1.2 Аппроксимирующая и детализирующая компоненты вейвлет-анализа и синтеза сигналов

Одна из основополагающих идей вейвлет-представления сигналов заключается в разбивке приближения к сигналу на две составляющие: грубую (аппроксимирующую) и уточнённую (детализирующую), с последующим их уточнением итерационным методом. Каждый шаг такого уточнения соответствует определённому уровню декомпозиции и реставрации сигнала. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами.

Такой подход нельзя назвать абсолютно новым. Он реализован давным-давно, к примеру, в технике представления функций рядами Тейлора или Фурье, а также в современной технике обработки изображений. В математических работах можно найти немало соотношений, по форме (но вовсе не по существу) напоминающих выражения для вейвлет-преобразований. Новым стало открытие целого класса функций, удовлетворяющих ряду особых условий и способных представлять произвольные функции, сигналы и изображения и обеспечивать повышенную в сравнении с рядами Фурье эффективность обработки последних.

Рассмотрим пространство функций , опреде­лённых на всей действительной оси и обла­дающих конечной энергией (нормой)

(1.7)

Функциональные пространства и существенно различны. В частности, локальное среднее значение каждой функции из должно стремиться к нулю на . Синусоидальная волна не принадлежит , и, следовательно, семейство синусоидальных волн не может быть базисом функционального простран­ства . Попробуем найти достаточно простые функ­ции для конструирования базиса пространства .

«Волны», образующие пространство должны стремиться к нулю на и для практических целей чем быстрее, тем лучше. Рассмотрим в качестве базисных функций вейвлеты  хорошо локализованные солитоно-подобные (солитон  решение нелинейного эволюционного уравнения, которое в каждый момент времени локализо­вана в некоторой области пространства, причём размеры области с течением времени остаются ограниченными, а движение центра области можно интерпретировать как движение частицы. Солитон уравнения Кортевега-де Фриза

описывает уединённую волну

и однозначно определяется двумя параметрами: скоростью и положением максимума в фиксированный момент времени «маленькие волны» (дословный перевод слова wavelet).

Как и в случае с пространством , которое полностью формировалось с помощью одной базисной функции , сконструируем функциональное простран­ство также с помощью одного вейвлета . Отметим, что это может быть вейвлет с одной частотой или с набором частот (frequency bands).

В основе непрерывного вейвлет-преобразования (НВП) лежит использование двух непрерывных и интегрируемых по всей оси (или функций:

• вейвлет-функция psi с нулевым значением интеграла определяющая детали сигнала и порождающая детализирующие коэффициенты;

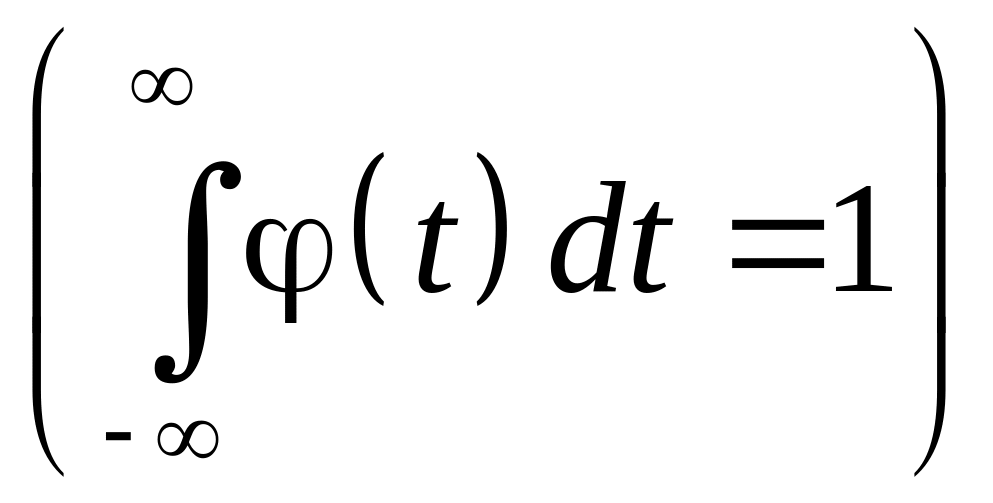• масштабирующая или скейлинг-функция phi с единичным значением интеграла определяющая грубое приближение (аппроксимацию) сигнала и порождающая коэффициенты аппроксимации.

Phi-функции присущи далеко не всем вейвлетам, а только тем, которые относятся к ортогональным. Остановимся только на свойствах psi-функции и на приближении ими локальных участков сигналов .

Psi-функция создаётся на основе той или иной базисной функции , которая, как , определяет тип вейвлета. Базисная функция должна удовлетворять всем тем требованиям, которые были отмечены для psi-функции . Она должна обеспечивать выполнение двух основных операций:

• смещение по оси времени при ;

• масштабирование  при и (в дальнейшем мы будем опускать выражение , означающее исключение значения .

Параметр задаёт ширину этого пакета, а  его положение. Иногда вместо явного указания времени используется аргумент , а вместо параметров и используются имеющие тот же смысл иные обозначения. Нетрудно убедиться в том, что следующее выражение задаёт сразу два этих свойства функции :

(1.8)

Таким образом, для заданных значений и функция и есть вейвлет. Вейвлеты, обозначаемые как , иногда называют «материнскими вейвлетами», поскольку они порождают целый ряд вейвлетов определённого рода.

(О вейвлетах, чётко локализованных в пространстве (или во времени), говорят, что они имеют компактный носитель).

Применительно к сигналам, как функциям времени, параметр задаёт положение вейвлета на временной оси, а параметр задаёт его масштабирование по времени.

В частотной области малые значения а соответствуют высоким частотам, а большие  низким частотам. Таким образом, операция задания окна, используемая в оконном преобразовании Фурье, как бы заложена в самой базисной функции вейвлетов. Это создаёт предпосылки их приспособления (адаптации) к сигналам, которые могут быть представлены совокупностью вейвлетов.

Довольно грубо можно представить вейвлеты как некоторые волновые функции, способные осуществлять преобразование Фурье не по всей временной оси (или оси , а локально по месту своего расположения. Для этого вполне естественно, что кроме изменения «средней частоты» маленькие волны должны перемещаться к тому месту сигнала или функции, в котором должно осуществляться «локальное преобразование Фурье». Хотя подобная интерпретация вейвлетов способна дать стимул к пониманию сути вейвлет-преобразований, она является чрезмерно упрощённой и подчас даже принципиально ошибочной. Прежде всего, потому, что подавляющее большинство вейвлетов не имеет ничего общего с модулированной по амплитуде синусоидальной волной.

Базисными функциями вейвлетов могут быть различные функции, в том числе, близко или отдалённо напоминающие модулированные импульсами синусоиды, функции со скачками уровня и т.д. Это обеспечивает лёгкое представление сигналов с локальными скачками и разрывами, наборами вейвлетов того или иного типа и открывает простор в подборе наиболее походящих вейвлетов, исходя из условий решаемых задач, и делает такое решение не тривиальным. К сожалению, почти все вейвлеты не имеют аналитического представления в виде одной формулы, но могут задаваться итерационными выражениями, легко вычисляемыми компьютерами.

Вейвлеты характеризуются своим временным и частотным образами. Временной образ определяется некоторой (детализирующей) psi-функцией времени. А частотный образ определяется её Фурье-образом , который задаёт огибающую спектра вейвлета. Фурье-образ определяется выражением:

Итак, с помощью вейвлетов сигнал представляется совокупностью волновых пакетов  вейвлетов, образованных на основе некоторой исходной (базовой, образующей и т.д.) функции . Эта совокупность, разная в разных частях временного интервала определения сигнала и корректируемая множителями, имеющими вид порой сложных временных функций, и представляет сигнал с той или иной степенью детализации. Такой подход называют вейвлет-анализом сигналов.

Число, используемых при разложении сигнала, вейвлетов задаёт уровень декомпозиции сигнала. При этом за нулевой уровень декомпозиции часто принимается сам сигнал, а последующие уровни декомпозиции образуют обычно ниспадающее вейвлет-дерево того или иного вида (иногда дерево задаётся «растущим» вверх). Точность представления сигнала по мере перехода на более низкие уровни декомпозиции снижается, но зато появляется возможность вейвлет-фильтрации сигналов, удаления из сигналов шумов и эффективной компрессии сигналов. Иными словами становится возможной вейвлет-обработка сигналов.