Лекция 3

3.1 Усреднение и детализация

Проще всего сжать изображение, если заменить это изобра­жение средним значением его пикселов. Этот подход даёт очень большую степень сжатия (одно число представляет все изображение), но немного даёт в плане качества изображе­ния. Чтобы восстановить исходное изображение из этого среднего значения, нам нужно знать, какие детали были уда­лены для получения этого значения. Рассмотрим изображе­ние, состоящее из двух точек . Эти значения могут быть заменены средним значением и полуразностью :

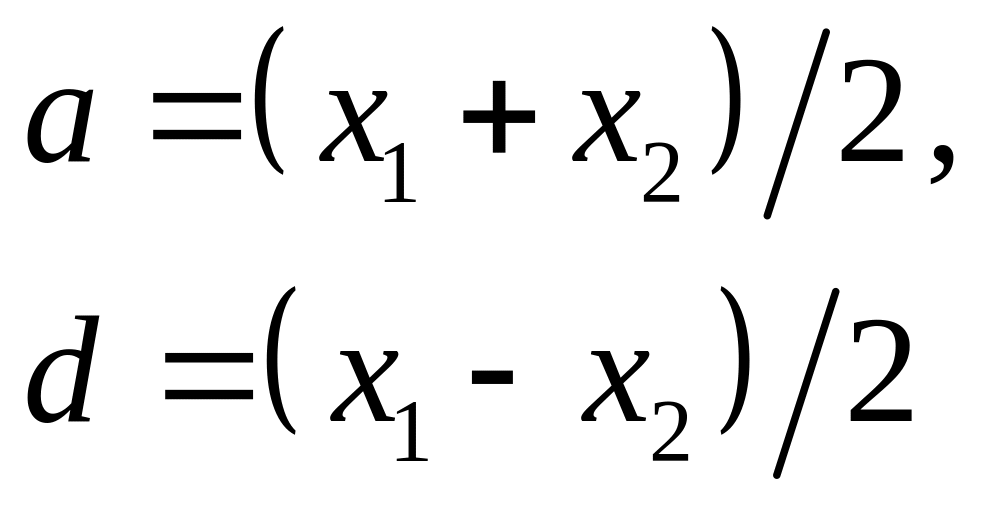
(коэффициент вводится в определение для удобства обо­значений). Заметим, что мы можем выразить через :

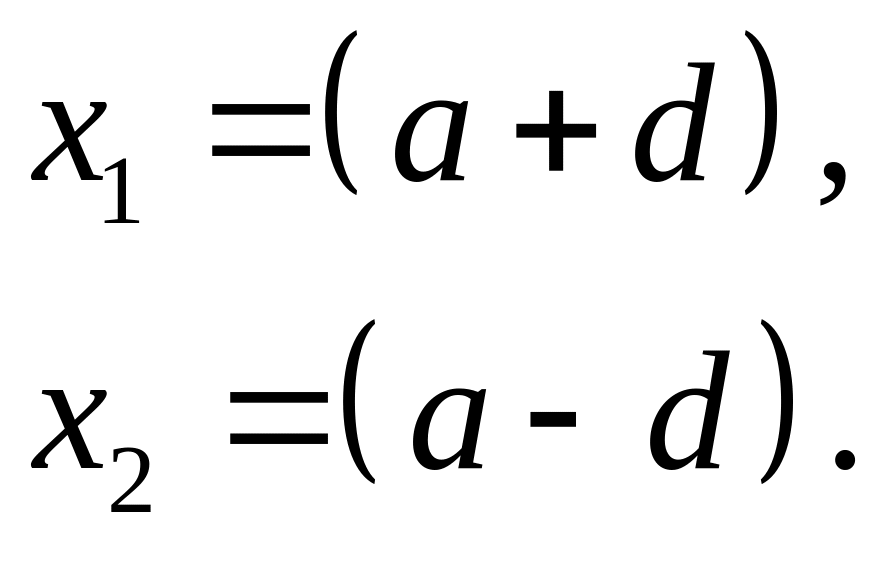
«Вейвлет-преобразование» исходной последовательности  это . Тогда возникает вопрос, как польза от замены на . Особенной пользы нет, если только два значения не оказываются близким друг к другу. В этом случае разность мала, и изображение можно заменить его приближением . Заметим, что это новое «изображение» имеет меньше пикселов, чем исходное. Мы получили сжатие изображения! Восстановленным изображением будет изображение с ошибкой изображения (error image) Так как мало, ошибка будет мала.

Основополагающей в вейвлет-анализе является идея о выде­лении информации при различных уровнях детализации. Де­тали, в свою очередь, могут рассматриваться как информация о масштабе или о разрешении. Простой пример, рассмотрен­ный выше, имеет ограниченную применимость к реальным изображениям, но он иллюстрирует идею, на которой осно­вывается применение вейвлет-анализа к сжатию изображе­ний: выделение информации, которую несут детали, и удале­ние тех информационных деталей, которые малы и незначи­тельно влияют на изображение в целом.

Рассмотрим несколько большее изображение Вычислим средние значения

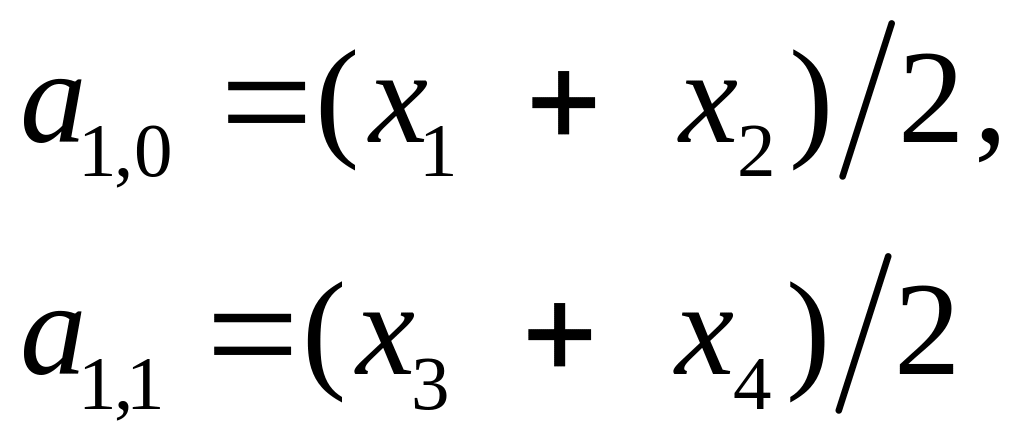(3.1)

и разности

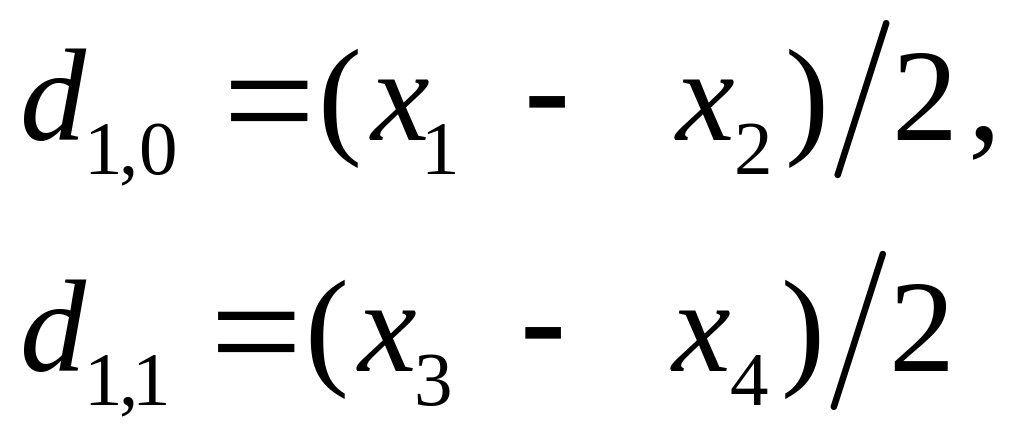(3.2)

(Двойные нижние индексы здесь показывают, что мы начинаем многошаговый процесс, и это его первый шаг). Как и раньше, мы получили новое представление исходного изображения, которое содержит ровно столько же пикселов, сколько и исходное. Если мы захотим сжать это изображение, мы обратим внимание на величину значений и решим, могут ли они без ущерба быть удалены. При этом мы получим сжатое изображение Предположим, однако, что нас не удовлетворяет такая степень сжатия и мы хотим сжать изображение сильнее. Тогда мы можем применить ту же процедуру к оставшемуся изображе­нию и снова вычислить среднее значение и раз­ность:

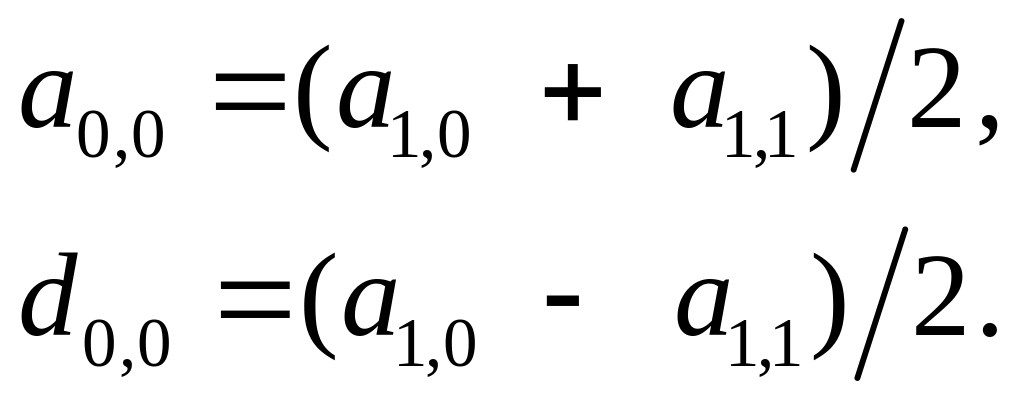(3.3)

Если разность достаточно мала, мы можем заменить все исходное изображение изображением, состоя­щим из одного единственного пиксела . Посмотрим, чем же является это

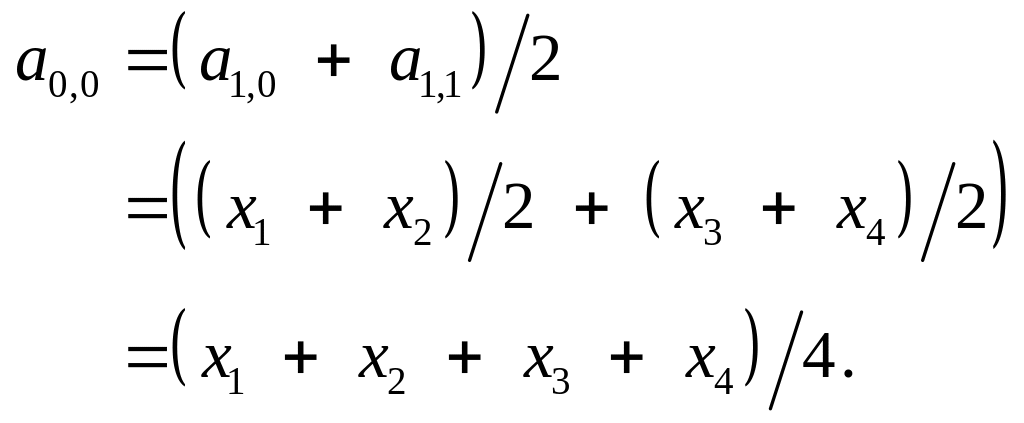(3.4)

Величина это всего лишь среднее значение всех пиксе­лов исходного изображения. Если исходное изображение од­нородно серое (т.е. все равны одному и тому же значению), то мы можем сжать его, заменив единственным значением, равным этой величине градации серого. Значение пред­ставляет самый приблизительный уровень информации об этом изображении, т.е. информацию при самом низком раз­решении или при самом грубом масштабе. Значения вместе взятые, представляют информацию на следую­щем, более высоком уровне разрешения, или при следую­щем, лучшем масштабе. Заметим, что мы можем восстано­вить из используя приведённую выше процедуру. Исходные значения пикселов пред­ставляют самое высокое разрешение или наилучший мас­штаб, возможный для этого изображения. Эти значения мо­гут быть восстановлены из Но так как мы можем получить то мы можем восста­новить значения пикселов исходного изображения из общего среднего значения и разностей Таким обра­зом, последовательность

(3.5)

является альтернативным представлением исходного изо­бражения и состоит из общего среднего и значений разно­стей, выражающих два различных уровня детализации. Последовательность (3.5)  это вейвлет-преобразование исходной последовательности . Заметим, что теперь мы имеем больше вариантов для сжатия. Если слишком велики, чтобы их игнорировать, то, возможно, мы можем исключить следующий уровень детализации, а именно,