В соответствии с вышеизложенным, общая схема имитационного моделирования имеет вид:

Рис. 6.1. Общая схема имитационного моделирования.

Обозначения: ГГР – генератор равномерно распределённых случайных чисел; П – преобразователь закона распределения; ФФ – формирующий фильтр; М – модель объекта или процесса; ИК – измерительный блок критерия функционирования объекта или процесса; БПЭ – блок планирования эксперимента;  - равномерно-распределённые случайные числа; x – случайные числа с заданным законом распределения; z – коррелированные случайные числа с заданной автокорреляционной функцией; y – случайные числа имитирующие выходную переменную объекта или процесса; U₁…U_k – управляемые переменные модели объекта или процесса; k - критерий функционирования моделируемого объекта или процесса.

2. Методы имитации случайных факторов при имитационном моделировании.

Имитационный системный анализ поведения сложных объектов и процессов выполняется с учётом воздействий внешней среды. Возмущающие воздействия внешней среды являются, как правило, случайными процессами с характерными законами распределения и автокорреляционными функциями. При имитационном моделировании случайных факторов и возмущающих воздействий необходимо получить случайную последовательность чисел, имеющих такой же закон распределения и такую же автокорреляционную функцию, что и закон распределения и автокорреляционная функция реальных возмущающих воздействий. Базовой последовательностью случайных чисел для решения этой задачи является совокупность случайных чисел с равномерным законом распределения:

,

(6.1)

Псевдослучайные числа  можно получать программно, например с использованием формулы:

(6.2)

где обозначает выделение дробной части числа, полученного в скобках.

Последовательность чисел с нормальным законом распределения может быть получена в соответствии с выражением:

(6.3)

где - математическое ожидание случайных чисел x; среднеквадратическое отклонение случайных чисел x; - равномерно распределённые случайные числа; - количество некоррелированных, случайных чисел с нормальным законом распределения.

Пусть автокорреляционная функция возмущающего воздействия имеет вид:

Рис. 6. 2. График автокорреляционной функции возмущающего воздействия.

Коррелированные случайные числа получают в соответствии с выражением:

(6.4)

где -номер коррелированного случайного числа; - параметры формирующего фильтра; - количество коэффициентов.

Параметры формирующего фильтра находятся путём решения системы уравнений:

, (6.5)

где -значения автокорреляционной функции, которые берутся из графика (рис. 6. 2.).

Система уравнений (6. 5) решается методом Ньютона. Приближение корней системы уравнений (6. 5) выполняется в соответствии с реккурентным соотношением Ньютона:

(6.6)

где - векторы к-го (к+1) приближения корней системы; - вектор, функция к-го приближения корней; - обратная матрица производных от вектор функции

Поиск вектора корней первого приближения выполняется в такой последовательности:

1. Задаются нулевым приближением корней то есть при К=0.

(6. 7)

2. Вычисляют значения вектор функции корней нулевого приближения:

(6. 8)

3. Вычисляют матрицу производных от вектор функции

(6. 9)

(6. 10)

С учётом (6. 9), получаем:

(6. 11)

В матрицу (6. 11) подставляют значения корней нулевого приближения и получим матрицу .

4. Обратную матрицу производных от вектор функции 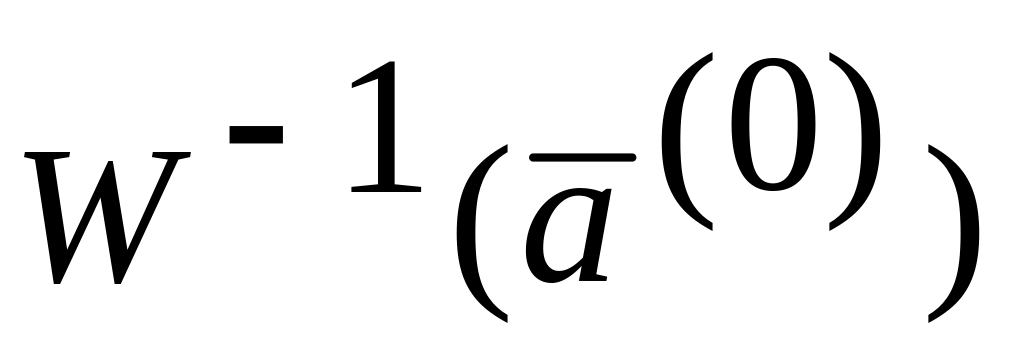получают методом Гаусса.

5. Подставляют значения в формулу (6. 6) и находят вектор корней нулевого приближения.

Аналогично находят векторы корней первого, второго и последующих приближений параметров формирующего фильтра.

Приближение корней выполняют до тех пор, пока:

(6. 12)

где - заданная точность вычислений.

Имитация случайных чисел с любым, кроме нормального, законом распределения может быть выполнена методом обратных функций. Он основан на использовании следующей теоремы.

Если х случайная величина, равномерно распределённая на отрезке [0;1], то случайная величина y является решением уравнения

, (6. 13)

Имеет плотность распределения где - заданный закон распределения реакции возмущающего воздействия.

Таким образом последовательность чисел x₀, x₁, x₂,…, x_i преобразуется в последовательность чисел y₀, y₁, y₂,…, y_i имеющую заданную плотность распределения .

Пример: Необходимо получить последовательность чисел, имеющих распределения по показательной функции:

В соответствии с (6.13) имеем:

,

откуда

.