26 Методы вычисления определенного интеграла. Формула Ньютона-Лейбница
Понятие определенного интеграла с переменным верхним пределом интегрирования, формула Ньютона-Лейбница. Теорема: Если ф-ия f (x) непрерывна для любого x [a; b], то производная от интеграла с переменным верхним пределом интегрирования по этой границе равна подынтегральной ф-ии от верхней границы интегрирования, то есть: Последствия: 1) Определенный интеграл с переменным верхним пределом от ф-ии f (x) является одним из первоначальных для f (x). 2) Любая непрерывная ф-ия на промежутке [a; b] имеет на этом промежутке первоначальную, которую, например, всегда можно построить в виде определенного интеграла с переменным верхним пределом.
27 Метод замены переменной для определенного интеграла
Теорема: Если: 1) f (x) - непрерывная для x [a; b], 2) () = а, () = b, 3) x = (t) и '(t ) - непрерывные для t [; ]; 4) при t [; ] x [a; b], то Замечание: При замене переменной интегрирования в определенном интеграле меняются пределы интегрирования и поэтому нет необходимости возвращаться к исходной переменной.
Вопрос 28. Интегрирование по частям определенного интервала
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
для определённого:
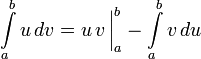
Формулы:
1. для неопределённого интеграла
Функции 
и 
гладкие,
следовательно, возможно дифференцирование:
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
Операция интегрирования обратна дифференцированию:
После перестановок:
Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точность до константы, возникающей во время интегрирования.
2. для определённого
В целом аналогично случаю неопределённого интеграла:
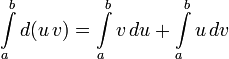
Пример: 
Вопрос 29. Вычисление площадей плоских фигур
Вычисление площадей плоских фигур производится с помощью формулы Ньютона-Лейбница
═ А
принадлежит отрезку от а до в══f(x)-непрерывна
x
=a,x=b;══
отр
[a,b] оси
оХ
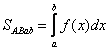
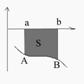
при
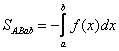
Н
о
бывают случаи, когда трапеция ограничена
двумя функциями:
Тогда формула будет трасформирована:
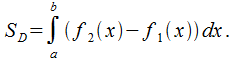
Вопрос 30. Несобственные интегралы I рода
Несобственные интегралы 1 рода.
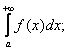
Введем определения для несобственных интегралов 1 рода.
Определение 1.
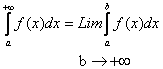
Если предел конечен, то несобственный интеграл 1 рода называется сходящимся;
Если предел бесконечен или не существует вовсе, то несобственный интеграл 1 рода называется расходящимся.
Есть в тетради.
Вопрос 31. Несобственные интегралы II рода
Несобственные интегралы 2 рода.
Определение 1.
Интеграл ви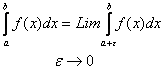да: 
,
где y=f(x) непрерывна (a;b], a - точка разрыва
2 рода. Называется несобственным
интегралом 2 рода.
Если предел конечен, то несобственный интеграл 2 рода называется сходящимся.
Определение 2.
Если предел равен бесконечности или не существует вовсе, то несобственный интеграл 2 рода называется расходящимся.
Пусть функция y=f(x) имеет разрыв 2 рода в точке C, принадлежащей (a;b). В остальных точках промежутка непрерывна.
Определение 3.
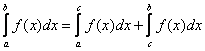
Если оба несобственных интеграла 2 рода справа сходятся, то несобственный интеграл слева называется сходящимся.
Если хотя бы один из интегралов справа расходится, то несобственный интеграл слева называется расходящимся.
Есть в тетради.