49. Функциональные ряды…… .
Определение 1. Выражение вида
,
(1.1)
где
- функции переменной
,
называется функциональным рядом.
Определение 2. Областью определения функционального ряда называется пересечение областей определения его членов.
Так, областью
определения ряда
является вся числовая прямая. Область
определения ряда
совпадает с множеством положительных
чисел.
Придавая в (1.1) переменной определённые числовые значения из области определения ряда, мы получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
Определение 3.
Точка
из области определения ряда называется
точкой сходимости функционального ряда
(1.1), если числовой ряд
(
)
(
)
…
(
)
…
(1.2)
сходится.
В противном случае называется точкой расходимости.
Определение 4. Совокупность тех значений , при которых функциональный ряд сходится, называется областью сходимости этого ряда.
Ясно, что область сходимости функционального ряда всегда является подобластью области определения этого ряда.
Очевидно, что в
области сходимости ряда его сумма
является некоторой функцией от
,
поэтому сумму функционального ряда
обозначают через
(
).
Пример. Рассмотрим функциональный ряд
Этот ряд сходится
при всех значениях
,
удовлетворяющих условию
так как для каждого значения
в интервале (-1;1) сумма ряда равна
(сумма бесконечно убывающей геометрической
прогрессии со знаменателем
).
Таким образом, в интервале (-1;1) данный
ряд определяет функцию
,
которая является суммой ряда, то есть
Отметим, что
естественная область определения
функции
шире области сходимости ряда
Определение 5.
Обозначим через
сумму первых
членов ряда (1.1)
.
Если ряд (1.1) сходится
и его сумма равна
,
то
,
где
Величина
называется остатком ряда (1.1).
Для всех значений в области сходимости ряда имеет место соотношение
,
поэтому
Определение 6.
Функция
называется представимой функциональным
рядом (1.1) на некотором промежутке
,
если:
функциональный ряд сходится при любом из этого промежутка и имеет сумму ;
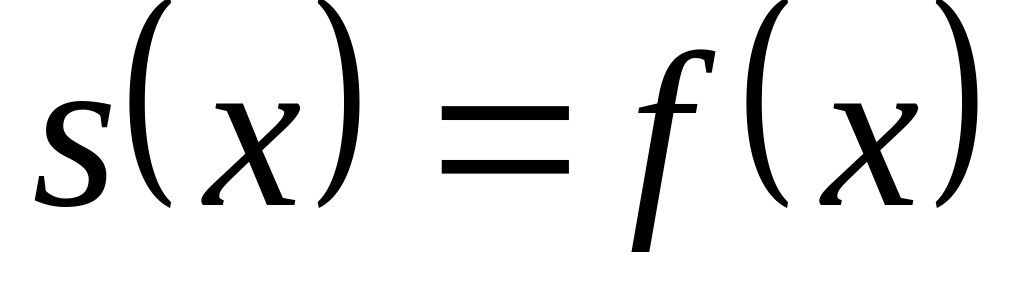для любого
.
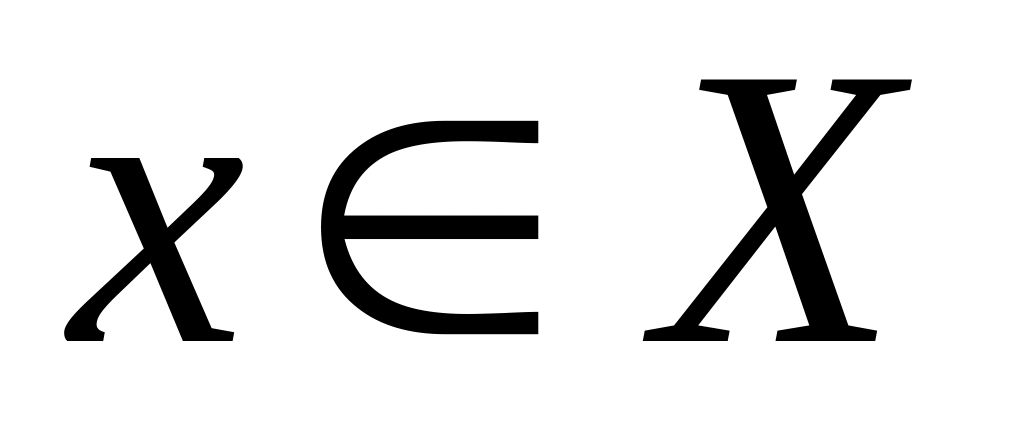Тот факт, что функция представима функциональным рядом, записывается так
.
50. Степенной ряд. Признаки сходимости. Область сходимости.
Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:
в котором коэффициенты an берутся из некоторого кольца R.
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема
Абеля: Пусть ряд
сходится в точке x0. Тогда этот ряд
сходится абсолютно в круге | x | < | x0 | и
равномерно по x на любом компактном
подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при x = x0, он расходится при всех x, таких что | x | > | x0 | . Из первой теоремы Абеля также следует, что существует такой радиус круга R (возможно, нулевой или бесконечный), что при | x | < R ряд сходится абсолютно (и равномерно по x на компактных подмножествах круга | x | < R), а при | x | > R — расходится. Это значение R называется радиусом сходимости ряда, а круг | x | < R — кругом сходимости.
Формула Коши-Адамара:
Значение радиуса сходимости степенного
ряда может быть вычислено по формуле:
(По поводу определения
верхнего предела
Пусть F(x) и G(x) — два степенных ряда с
радиусами сходимости RF и RG. Тогда
Если у ряда G(x) свободный член нулевой, тогда
Вопрос о сходимости ряда в точках границы | x | = R круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
Признак Д’Аламбера: Если при n > N и α > 1 выполнено неравенство
тогда степенной ряд сходится во всех точках окружности | x | = R абсолютно и равномерно по x.
Признак Дирихле: Если все коэффициенты степенного ряда положительны и последовательность an монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности | x | = 1, кроме, быть может, точки x = 1.
Вторая теорема Абеля: Пусть степенной ряд сходится в точке x = x0. Тогда он сходится равномерно по x на отрезке, соединяющем точки 0 и x0.
Сумма степенного ряда как функция комплексного параметра x является предметом изучения теории аналитических функций.