19.Интегралы вида

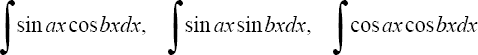
находятся с помощью тригонометрических формул

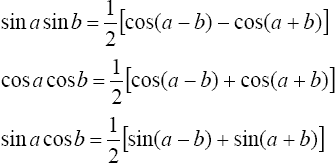
20.Вычисление интегралов вида   , где m и n ? целые числа.

В этом случае полезно пользоваться следующими правилами:

А) если m - нечетное положительное число, то вносим   под знак дифференциала или, (что то же самое) делаем замену переменной   . При этом число n может быть рациональной дробью. Аналогично, если n - нечетное положительное число, то вносим под знак дифференциала   или применяем подстановку   . Сравни с 1. Смотри 

Б) если оба показателя m и n - четные положительные числа, то подынтегральную функцию преобразуют с помощью формул понижения степен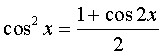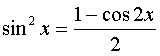и:   ,   и   .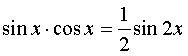

В) если число m+n является четным отрицательным числом, то можно сделать замену переменной   или   . Смотри пример 6 .

Г) если степени m и n отрицательны, то часто бывает полезным уменьшить степени с помощью основного тригонометрического тождества. Смотрипример 7 .

Примечание. В общем случае интегралы вида   , где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые выводятся путем интегрирования по частям.

21.Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок

Рассмотри интегралы, содержащие квадратный трехчлен:

.

Выделив полный квадрат под корнем, получим один из трех интегралов: , , . Все они вычисляются с помощью тригонометрических подстановок.

1.

.

2.

.

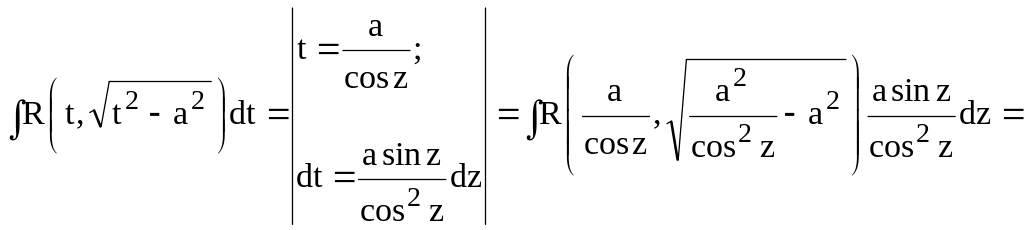
3.

.

22Интегрирование простейших иррациональных выражений

.Класс иррациональных функций очень широк, поэтому универсального способа их интегрирования просто быть не может. В этой статье попытаемся выделить наиболее характерные виды иррациональных подынтегральных функций и поставить им в соответствие метод интегрирования.

1.Используя метод непосредственного интегрирования, достаточно просто находятся неопределенные интегралы вида ,

где p – рациональная дробь, k и b – действительные коэффициенты.

2.Бывают случаи, когда уместно использование метода подведения под знак дифференциала. Например, при нахождении неопределенных интегралов вида  , где p – рациональная дробь.

3.Достаточно часто приходится иметь дело с неопределенными интегралами вида 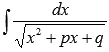 , где p и q – действительные коэффициенты. В этом случае выделяем полный квадрат под знаком корня: 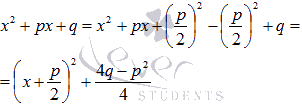и используем формулу из таблицы неопределенных интегралов  . 4.Нахождение множества первообразных иррациональных функций  , где M, N, p и q – действительные коэффициенты, очень схоже с интегрированием простейших дробей третьего типа: выполняется подведение под знак дифференциала, затем выделяется полный квадрат подкоренного выражения и применяются формулы из таблицы первообразных

24 Понятие интегральной суммы

Понятие интегральной суммы естественно обобщается на случай знакопеременной функции. В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл ( гл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом. В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл ( гл. На основе задачи об определении объема тела мы тию двумерной интегральной суммы, предел которой называется двойным интегралом. В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл ( гл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным, интегралом. В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл ( гл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом. В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл ( гл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным, интегралом. Исторически возникло два подход к теории интеграла для функции одной переменной. Первый подход, связанный с именем Ньютона, характеризуется тем, что исходной в теории интеграла считается задала обращения операции дифференцирования, т.е. задача определения функции по ее производной. Второй подход, исходящий от Лейбница, опирается на понятие интегральной суммы. Интеграл функции, есть предел ее интегральных сумм. Логическое завершение этого подхода к понятию интеграла дает теория интеграла Римана, которая обычно и излагается в большинстве руководств пб математическому анализу. Широкое применение находят наглядные пособия и ТСО на уроках повторения и обобщения материала по всей изученной теме. Если в кабинете математики имеются кинофильмы или диафильмы, содержание которых соответствует данной теме, то их можно использовать полностью. Для обобщения материала полезно использовать экранные пособия и по другим темам, непосредственно связанным с данной. Например, при повторении темы Объемы тел целесообразно использовать материалы, которые иллюстрируют понятие интегральных сумм и их применение в алгебре и началах анализа.

25 Свойства определенного интеграла 1) Если f (x) = c = const, то 2) Устойчивое множитель можно выносить из-под знак определенного интеграла. 3) Если f1 (x) и f2 (x) интегрируемые на [a; b], то: 4) Если в определенном интеграле поменять местами пределы интегрирования, то интеграл только изменит свой ​​знак на противоположный. 5) Определенный интеграл с одинаковыми пределами интегрирования равен нулю. 6) Если f (x) - интегрируема в любом из промежутков [a; b], [a; c], [c; b], то: 7) Если f (x)  0 и интегрируема для x  [a, b], b> a, то 8) Если f (x), g (x) - интегрируемые и f (x)  g (x) для x  [a; b], b> a, то: 9) Если f (x) - интегрируема и m  f (x)  M, для x  [a; b], b> a, то 10) (Теорема о среднем): Если ф-ия f (x) - непрерывная для x  [a; b], b> a, то найдется такая точка x = c  [a; b], что: