1.7. Властивості транспонування

1. 

для довільної матриці А (ідемпотентність);

2. ,

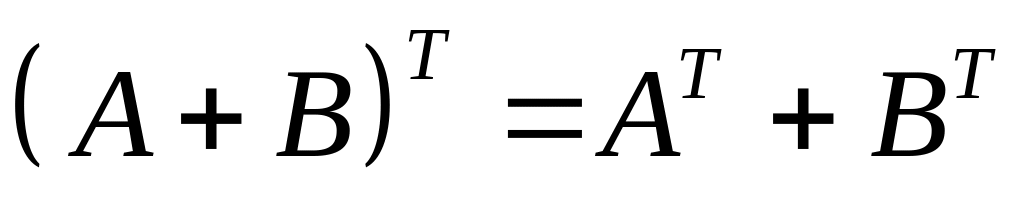де А і В – довільні матриці однакових розмірів (адитивність);

3. 

для довільної матриці А і довільного числа λ (однорідність);

4. 

для довільних матриць А і В, для яких існує добуток АВ;

5. .

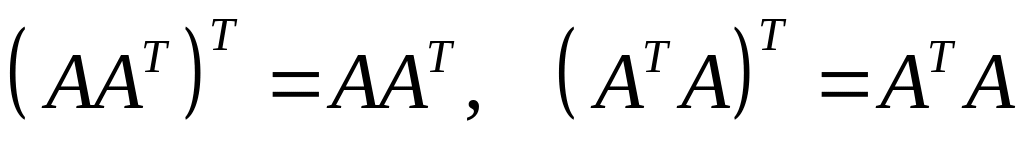Доведемо ці властивості.

1. Очевидно.

2. Справді,

=

3. Справді,

4. Нехай U = АВ. Тоді

тобто = .

5. Доведемо першу з рівностей. Використаємо попередню і першу властивості:

.

Матриця А, для якої , називається симетричною.

Таким чином, матриця завжди симетрична.

Приклад:

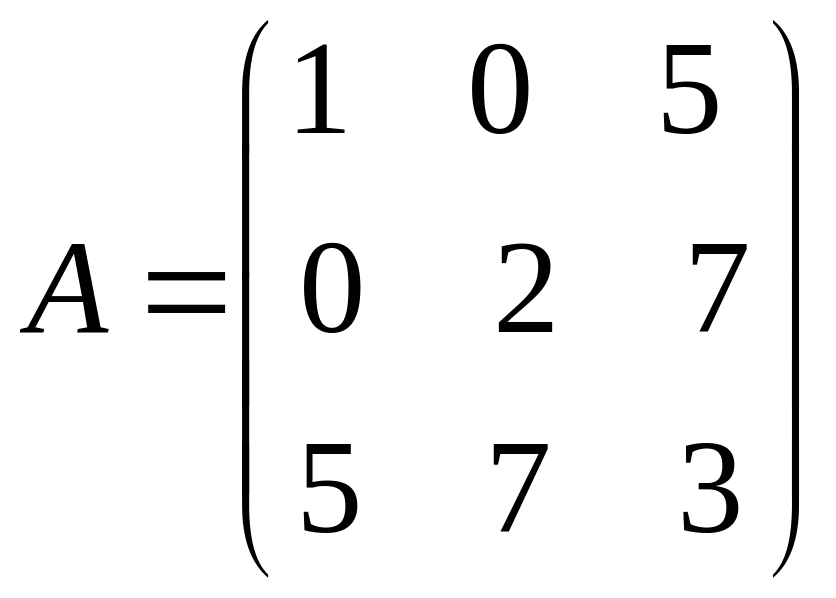– симетрична матриця.

1.8. Обернена матриця у випадку квадратних матриць другого порядку

Приклад.

Розглянемо матрицю . Припустимо, що матриця А має обернену матрицю . Тоді , тобто

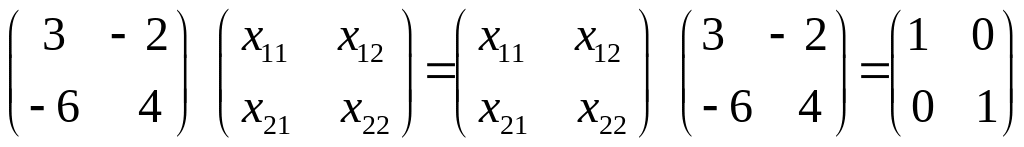. З рівності отримаємо дві системи:

і

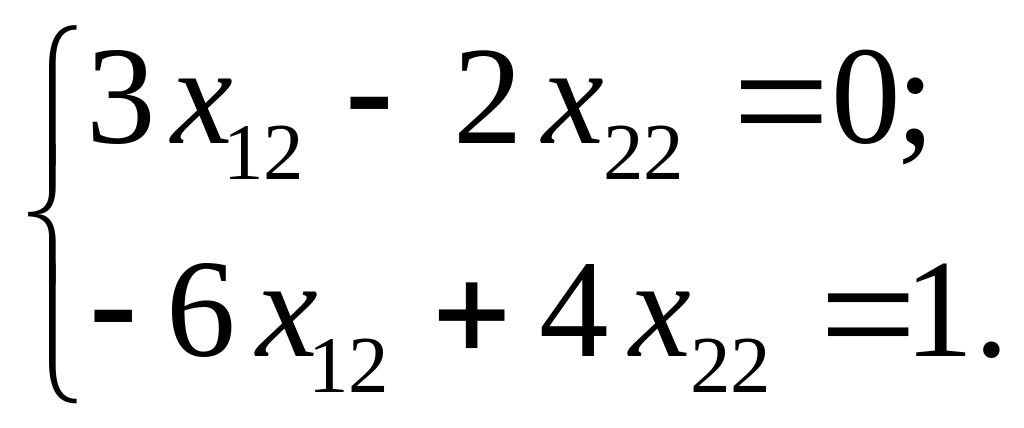
Оскільки то , тобто Очевидно, що така рівність і друга рівність системи виконуватися одночасно не можуть. Отже маємо протиріччя. Таким чином, матриця А оберненої матриці не має.

Приклад.

Нехай матриця . Покажемо, що А має обернену матрицю і знайдемо її.

Існування матриці, оберненої до А, рівносильне існуванню спільного розв’язку двох матричних рівнянь і , де

.

Припустимо, що такий розв’язок справді існує, тоді з отримаємо системи:

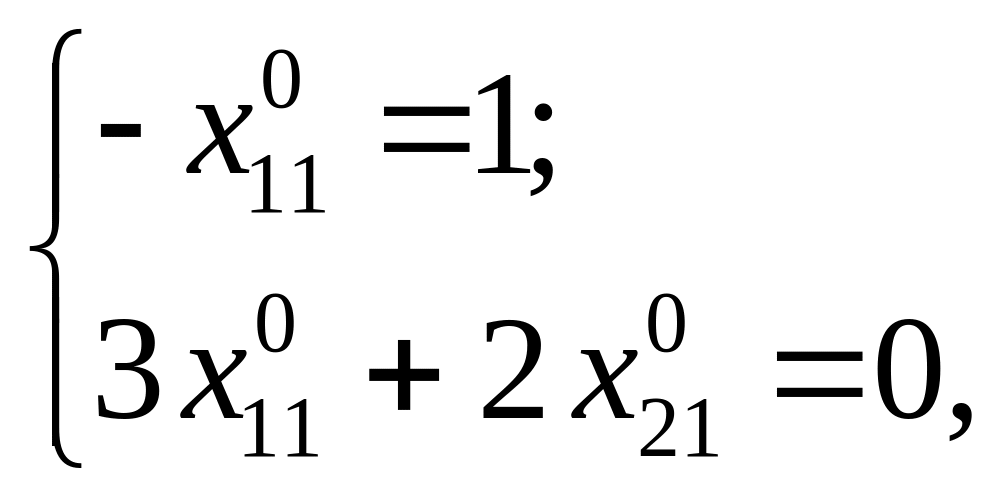
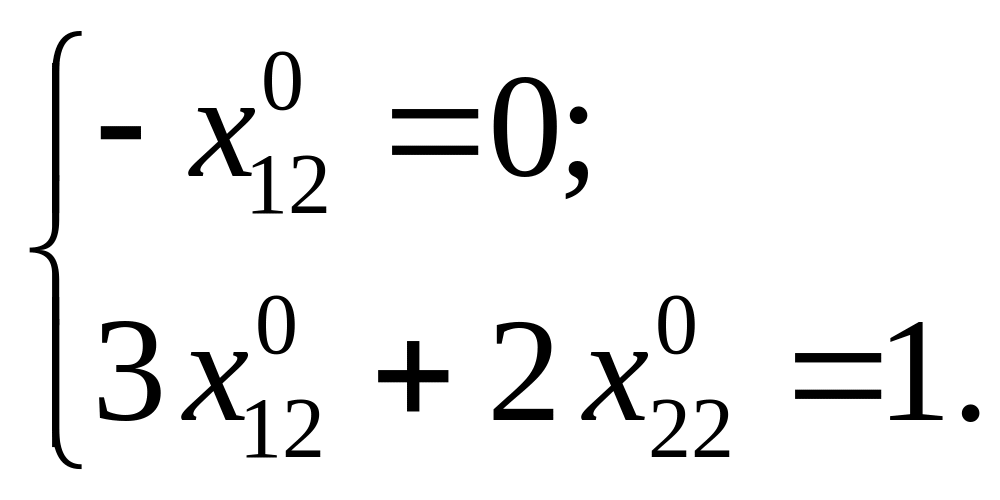
Зрозуміло, що тоді

Отже, з існування розв’язку випливає, що він дорівнює .

Легко переконатися, що справді

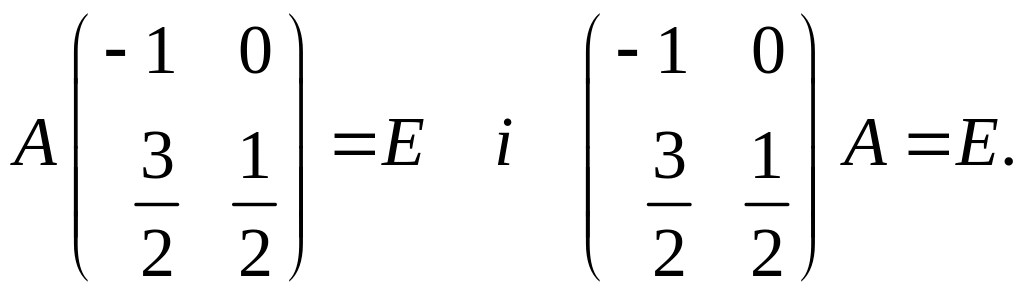
Таким чином існує і дорівнює

Для кожної квадратної матриці другого порядку існує простий спосіб з’ясування того факту, чи існує для неї обернена матриця. Для цього введемо поняття визначника квадратної матриці другого порядку.

Визначником матриці називається число

.

Зрозуміло, що .

Лема. Якщо А і В – дві квадратні матриці другого порядку, то

Доведення. Справді,

= =

–

–

=

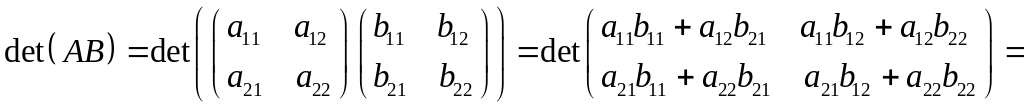
Лему доведено.

Твердження. Для того, щоб квадратна матриця А другого порядку мала обернену матрицю, необхідно і достатньо, щоб

Доведення. Нехай матриця А має обернену матрицю В. Тоді АВ = ВА = Е, де .

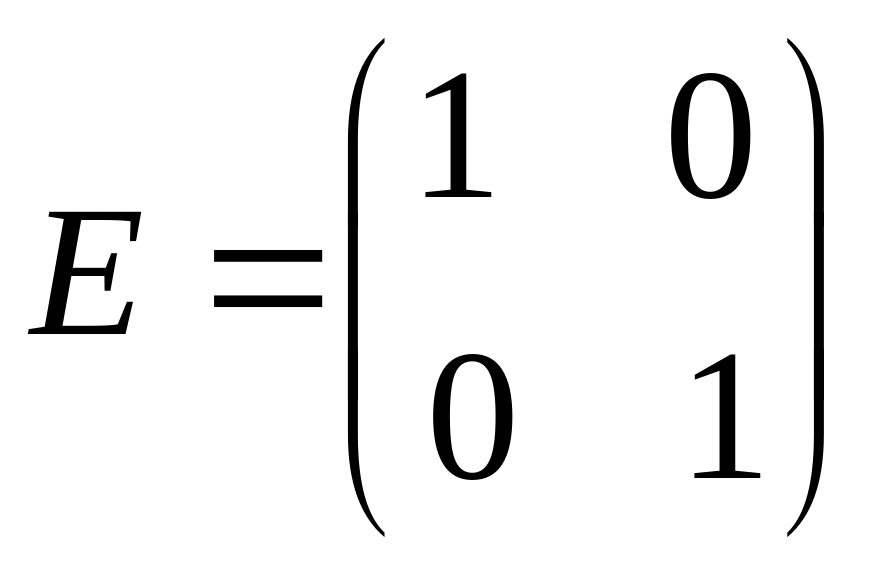За лемою 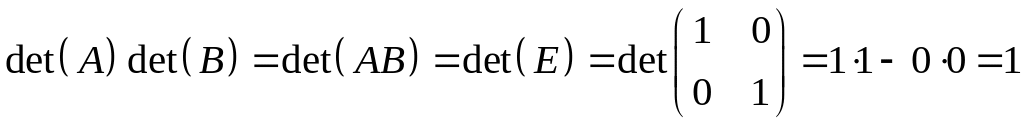, тобто . Тому

Навпаки, нехай Покажемо, що матриця

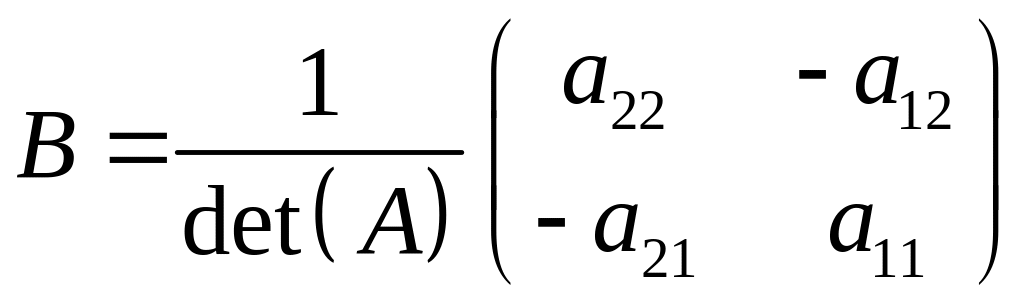є оберненою до А. Справді,

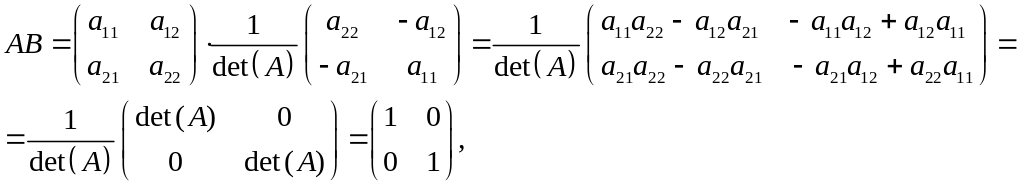
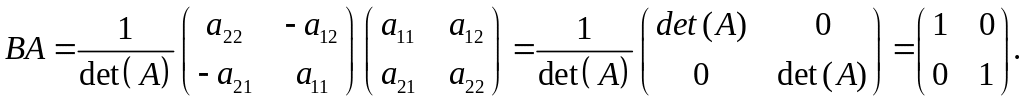
Твердження доведено.

Приклад.

Нехай Тоді

Отже, А має обернену матрицю

.

Приклад.

Нехай 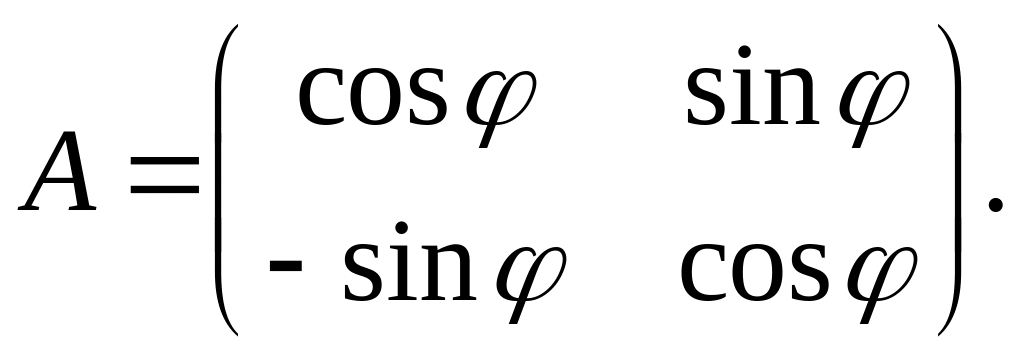Тоді

Отже, існує і дорівнює матриці .

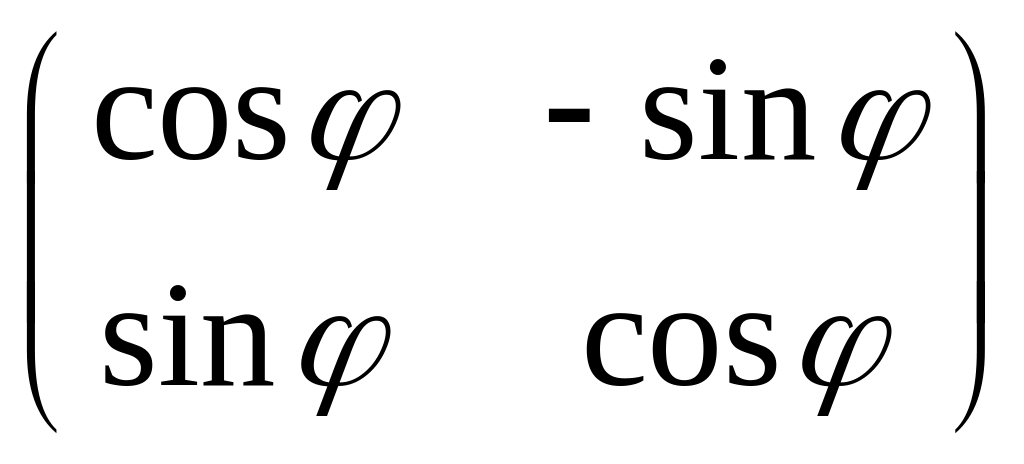Квадратна матриця А другого порядку називається особливою (або виродженою), якщо і неособливою (невиродженою), якщо

1.9. Приклади матриць, елементами яких є вектори

До цього часу ми розглядали лише такі матриці, елементами яких є числа. Проте в математиці використовуються також і матриці, елементами яких є самі матриці. Неявно ми вже використовували їх, коли визначали добуток двох матриць. Справді, нехай матриця А має розмір а матриця тоді

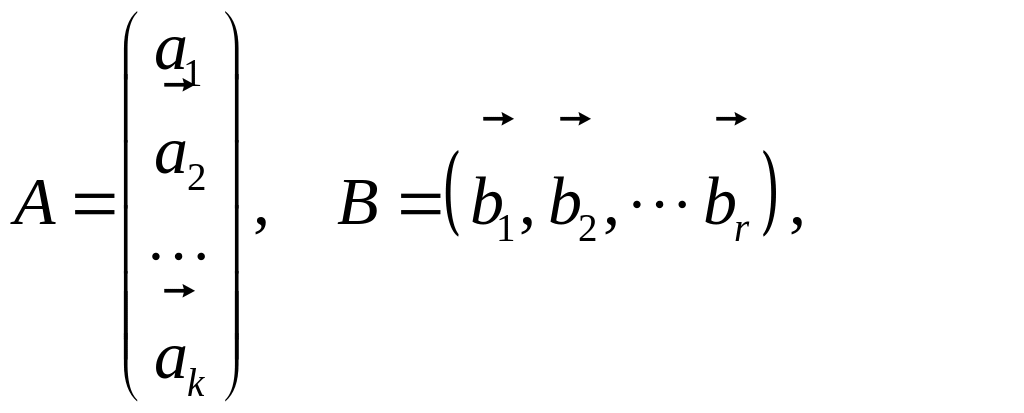(1)

де - рядок матриці А, а – стовпець матриці . Тоді АВ ми визначали, як

(2)

де

Якщо б в (1) ми вважали б звичайними числами і визначали б добуток А і В звичайним способом (за означенням добутку матриць, елементами яких є числа), то ми також одержали б добуток АВ, визначений формулою (2). Ці міркування можна поширити на більш загальний випадок матриць, елементами яких є матриці. Проте тут ми цього робити не будемо, а лише обмежимося конкретними прикладами.

Приклад 1.

Нехай - двовимірні вектори, - числа. Тоді

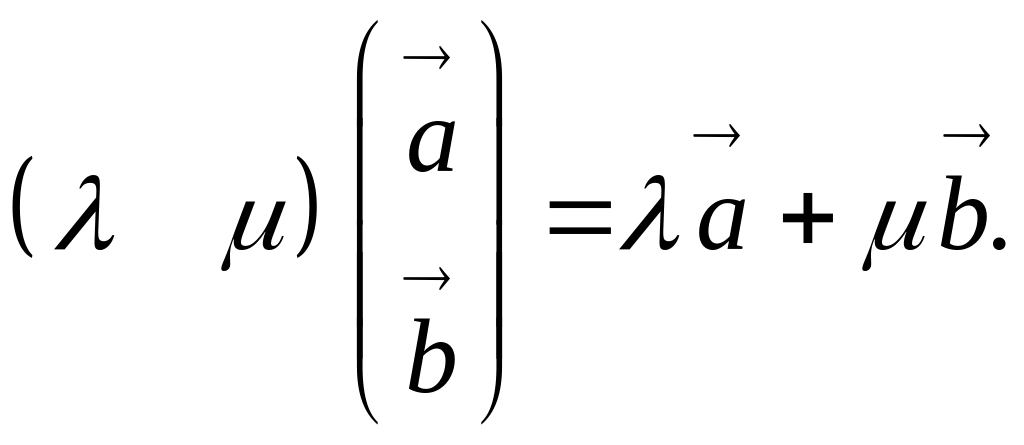
Справді,

Приклад 2.

Нехай – двовимірні вектори, 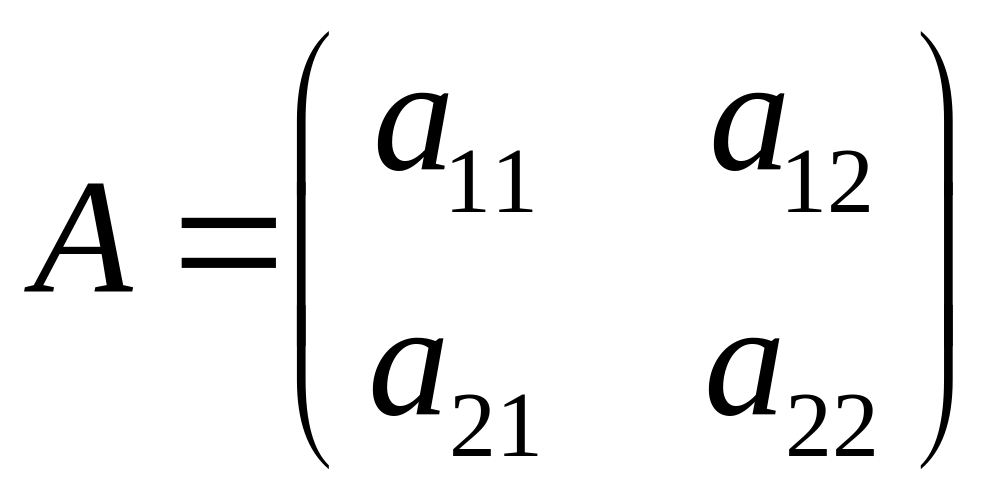– матриця з числовими елементами. Тоді

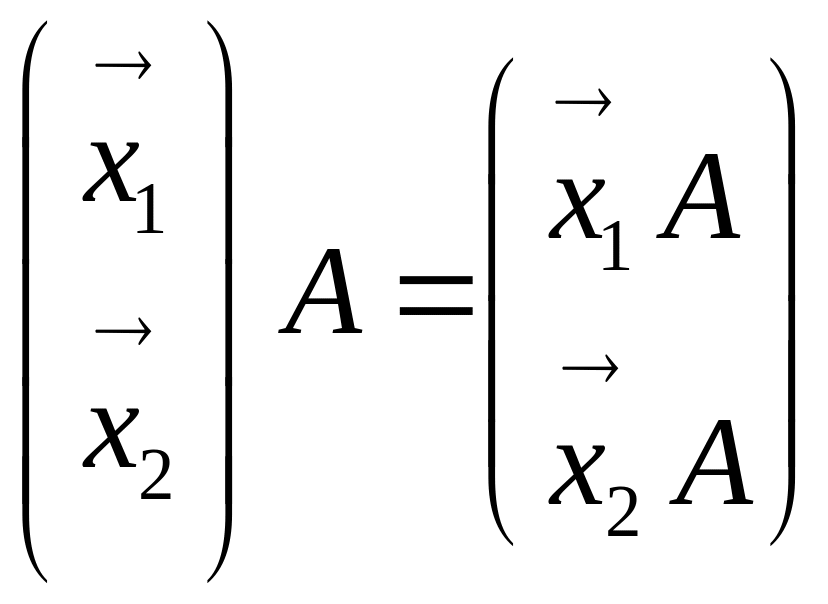
(тут на А можна дивитися як на матрицю з елементом А, при цьому, очевидно, добутки будуть визначені).

Справді, .

Приклад 3.

Нехай 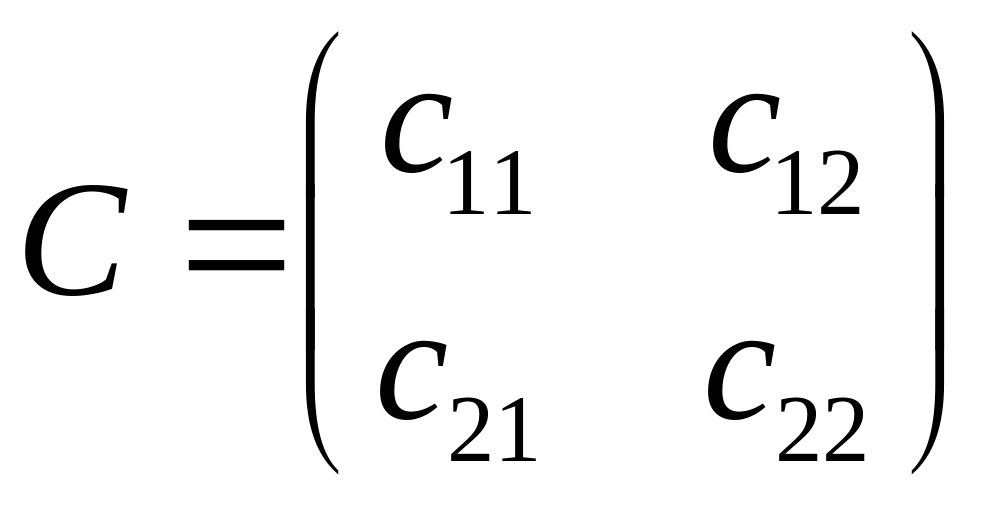– матриця з числовими елементами, а – двовимірні вектори. Ми не можемо визначити подібно до того, що було в прикладі 2, оскільки не будуть визначені, однак

Справді,

Доведемо тепер одне твердження, яке буде потрібне нам далі.

Твердження. Нехай А – матриця – двовимірні вектори і виконуються рівності:

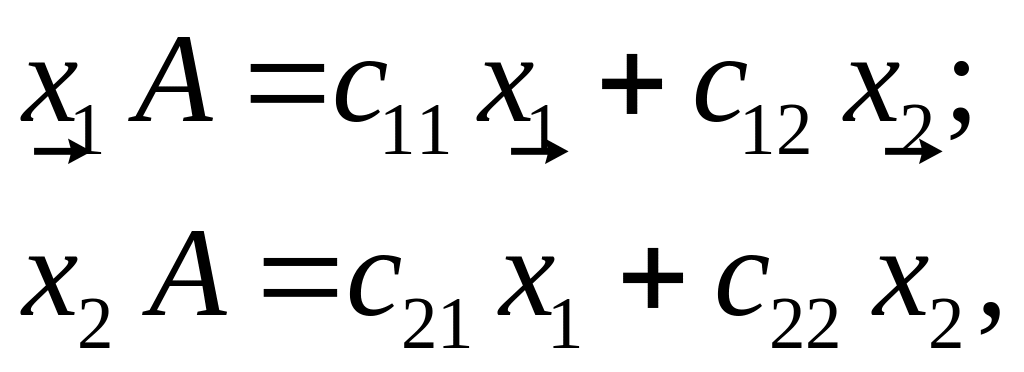(3)

де – деякі числа Якщо , то ,

де

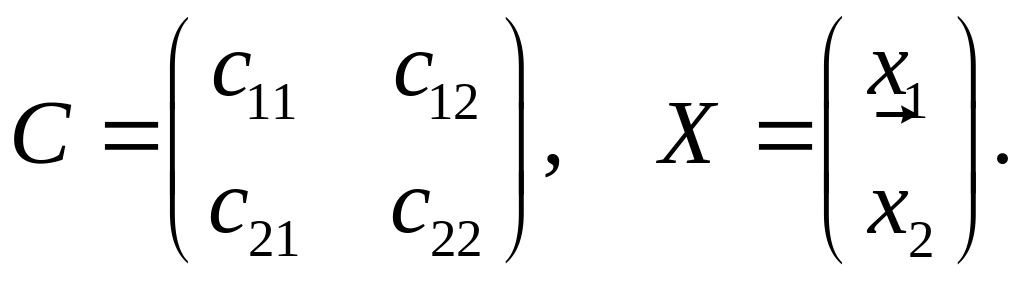
Доведення. Використаємо попередні приклади. З рівностей (3) отримаємо, що

Тоді з прикладів (2) - (3) маємо, що

тобто

З твердження про необхідну і достатню умову існування оберненої матриці випливає існування . Отже,