Окна изображений.

Функция plot автоматически открывает новое окно изображения, если до этого его не было на экране. Если же окно существует, то plot использует его по умолчанию. Новое окно открывается по команде figure. Если окон изображения несколько, то для выбора одного из них в качестве текущего окна следует использовать команду figure(n), где n – это номер в заголовке окна. Результаты всех команд будут выводиться в текущее окно.

Окно изображений обладает широким набором средств редактирования созданного графика. Для перехода в режим редактирования достаточно щелкнуть на кнопке  (Edit Plot) или выбрать аналогичный пункт из меню Tools. Затем можно выделить объект редактирования и либо использовать команды меню Edit (правка), Insert (вставка), Tools (сервис) либо вызвать контекстное меню и изменить свойства объекта.

Добавление кривых на существующий график.

Команда hold позволяет добавлять кривые на существующий график. Она используется в следующих формах:

• hold on обеспечивает продолжение вывода графиков в текущее окно;

• hold off отменяет режим продолжения;

• hold работает как переключатель с одного режима на другой.

Построим в качестве примера график функции sin(x) и с помощью команды hold on наложим на него график многоугольника:

x=-5:.1:5;

plot(x, sin(x));

axis equal

hold on

t = 0:pi/10:2*pi;

plot(3*exp(i*t), '-o')

В данном примере аргумент функции plot является комплексным числом. В этом случае происходит построение графика зависимости реальной части аргумента от его мнимой части. Вершины многоугольника обозначены маркерами в виде кружков.

Управление осями.

По умолчанию графики выводятся без указания наименований осей в режиме автоматического масштабирования. При этом масштабные коэффициенты пропорциональны размерам графического окна, что позволяет использовать пространство окна оптимальным образом. Функция axis используется для настройки масштаба, ориентации и коэффициента сжатия. Рассмотрим некоторые варианты применения команды axis:

• axis([xmin xmax ymin ymax]) – установка диапазонов координат по осям x и y для двумерного графика;

• axis auto – установка параметров осей по умолчанию;

• axis – возвращает вектор строку с текущими диапазонами координат;

• axis manual – замораживает масштабирование в текущем состоянии, чтобы при использовании команды hold on следующие графики использовали те же параметры осей;

• axis tight – устанавливает диапазоны координат по осям в соответствии с диапазонами данных;

• axis ij – задает систему координат с началом в левом верхнем углу;

• axis equal – включает масштаб с одинаковым расстоянием между метками по осям x, y и z;

• axis square – устанавливает текущие оси в виде квадрата (или куба в трехмерном случае);

• axis off – убирает с осей их обозначения и маркеры;

• axis on – восстанавливает ранее введенные обозначения осей и маркеры.

Нарисуем эллипс в режимах axis auto, который используется по умолчанию, axis square, который делает оси x и y равными и axis equal, который делает единицы измерения на осях равными:

t = 0:pi/20:2*pi;

subplot(1,3,1);

plot(sin(t), 2*cos(t))

grid on

subplot(1,3,2);

plot(sin(t), 2*cos(t))

grid on

axis square

subplot(1,3,3);

plot(sin(t), 2*cos(t))

grid on

axis equal

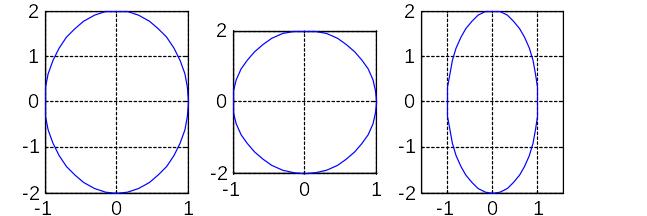
Для того, чтобы координатные оси вплотную примыкали к эллипсу, следует использовать опцию tight, например: axis equal tight.