22. Лінійні порівняння з однією змінною. Теорема про число розв’язків. Метод розв’язування лінійних порівнянь.

Озн. Порівняння першого степеня з однією невідомою величиною називається .(1) називають розв’язком рівняння, якщо при його підстановці рівняння перетворюється в істинне числове порівняння.Теорема1:Якщо am-взаємнопрості то рівність(1) маэ і притому єдиний розв’язок.

Д-ня: Розглянемо повну систему найменших невід’ємних лишків. ПСННЛ(modm)={0,1,2…m-1}так як am-взаємнопрості, то згідно теореми про ПСЛ, якщо х пробігає ПСЛ то ax-b теж пробігає ПСЛ причому лише один раз ax-b буде порівнюватись з 0(modm) .

Теорема2:Якщо найбільше CD(a,m)=d i то(1)не має розв’язків.

Д-ня: (від супротивного) з даної нерівності так, як ,а це суперечить умові.

Теорема3:Якщо НСД(a,m)=d і то рівність має d- розв’язків за mod(m).НСД(a,m)=d

так як взаємно прості, то згідно Теореми1 порівняння має єдиний розв’язок. цей клас розбиваємо за (modm), які будуть розв’язками порівняння. Основними методами розв’язування порівнянь є:

1.Безпосередня перевірка лишків ПСННЛ. Цей метод використовується тоді коли(modm)порівняно невелике число.

2.полягає в тому, щоб використати властивість порівнянь одержати коефіцієнт х.

23.Застосування теорії порівнянь до виведення ознак подібності.

Подільність двох чисел на множину натуральних чисел є бінарним відношенням, є транзитивне: ,антисиметричним:

.Ознака подільності означає, замінити подільність натуральних чисел, подільністю малих натуральних чисел. Кожне натуральне число можна записати так:

Причому - це цифри десяткової системи. (modm)>1.Знайдемо остачу від ділення основи систем числення в різних степенях на m.

Таким чином ми довели Теорему Паскаля. Теорема: число то і якщо b ділиться на ь то і а ділиться на m.

Ознака : на(2:5)Так як 10 і будь-яка степінь 10 ділиться націло на 2 і 5 то остача їх від ділення на 2:5=0.Для того щоб число а ділилось націло на 2 і 5 необхідно і достатньо, щоб його остання цифра ділилась націло і на 2 і на 5.

Ознака подільності: на(3і9)

число а:3 тоді і тільки тоді коли сума його цифр ділиться на 3.Число а:9 тоді і тільки тоді коли сума його цифр ділиться на 9.

Ознака подільності:на 11.

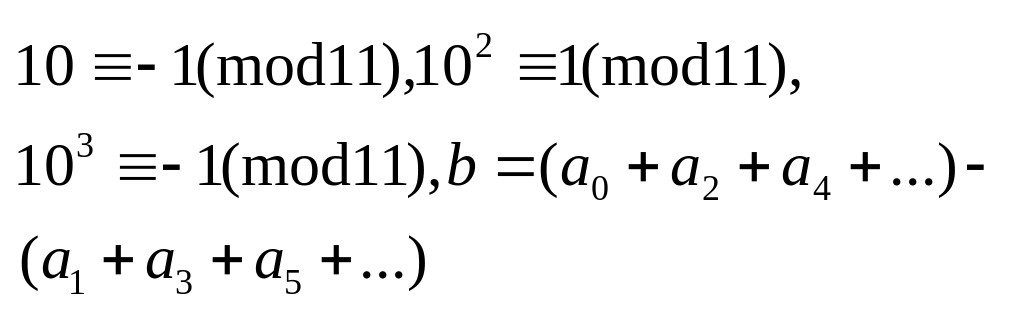
Число а:11тоді і тільки тоді коли різниця суми цифр які стоять на непарних місцях, і суми цифр, що стоять на парних місцях діляться на 11.

25. Многочлени над полем. Теорема про ділення з остачею. Нсд двох многочленів. Алгоритм Евкліда.

Озн. Нехай Р деяке числове поле. Полем називається не порожня множина Р-елементів довільної природи, яка містить принаймні два різних елементи, введені дві бінарні операції «+», «*» і виконується 7 вимог:

1.а+в=в+а 2.(а+в)+с=а+(в+с)

3. 4. 5.

6. 7. .

Означення: многочленом n-го степеня над числовим полем Р називається вираз виду

Причому всі елементи ,а також х належать одному полю Р.

Теорема про ділення з остачею: Які б не були два многочлени P(x) i Q(x) які не дорівнюють існують і притому єдині многочлени S(x) i R(x) для яких виконується рівність D(x)=Q(x)S(x)+R(x), degR(x)<degQ(x), S(x)-частка, R(x)-остача

Нехай Р(х) многочлен 0-степеня і степеня тоді S(x)=a,Q(x)=b.

В загальному випадку доведемо теорему ММІ по n.

1.якщо n>0 то цей випадок ми довели.

2.Припустимо що теорема істина при n-1 і доведемо для n.Введемо допоміжно n=1.

Підрахуємо степінь многочленна Ф(х),degP(x)=n,

Старший член многочленна Р(х) є і старший член другого доданка Ф(х) є .В многочленні Ф(х) старшим членом буде доданок степінь якого буде n-1, а за припущенням 2-го пункту ММІ теорема істинна тобто Ф(х)=Q(x)+R(x), degR(x)<degQ(x).

Доведемо єдність: Припустимо, що є два різні представлення P(x)=Q(x)S(x)+R(x),

degR(x)<degQ(x);

Очевидно, що deg лівої частини більший deg правої частини.Так як степені різні то рівність можлива лише тоді коли

Теорему доведено. Теорема Безу: Остача від ділення многочленна Р(х) на многочлен Q(x)=P( ).

Згідно теореми існують такі єдині многочлени S(x) i R(x), що має рівність

Доведенно.

d(x)-спільний дільник P(x)iQ(x) якщо і P(x)iQ(x) ділиться без остачі на многочлен d(x).Спільний дільник d(x)який має ділитись на всі інші спільні дільники називається найбільшим спільним дільником P(x)iQ(x).(НСД).

Якщо многочлен P(x) ділиться без остачі на многочлен Q(x) то для будь-якого не 0 числа C P(x) ділиться без остачі і на C*Q(х). Таким чином подільність многочленна визначається з точністю до сталого множника дійсного числа. Ми будемо вважати, що НСД двох многочленів є єдиним многочленом в розумінні з тотожністю до сталого множника яким є многочлен 0-степеня.

Алгоритм Евкліда для P(x)iQ(x):

P(x)-ділене Q(x)-дільник (х)-частка -остача.

1. є 0-многочленом,це означає що P(x) ділиться на Q(x).Очевидно що НСД цих многочленів. Якщо не є 0-многочленом маємо

. Два випадки:

1. тоді НСД

Без остачі значить НСД= .Якщо не є 0-многочленом то поділимо на .

І проводим аналогічно.Очевиднго,що цей процес є скінченним і містить не більше ніж n-кроків.

Провівши міркування проведені аналогічно до перших отримаємо НСД(P(x)iQ(x))=R(x).

Означення: Записані вище рівності називаються алгоритмом Евкліда для P(x) i Q(x).Теорема Евкліда: НСД(P(x)iQ(x)) називається остання відмінна від 0-многочлена остача алгоритму Евкліда.