Алгоритмы Брезенхема растровой дискретизации окружности и эллипса

Алгоритм изображения окружности несколько сложнее, чем построение отрезка. Мы рассмотрим его для случая окружности радиуса с центром в начале координат. Перенесение его на случай произвольного центра не представляет труда. При построении растровой развертки окружности можно воспользоваться ее симметрией относительно координатных осей и прямых . Необходимо сгенерировать лишь одну восьмую часть окружности, а остальные ее части можно получить путем отображений симметрии. За основу можно взять часть окружности от 0 до 45⁰ в направлении по часовой стрелке с исходной точкой построения . В этом случае координата окружности является монотонно убывающей функцией координаты .

П ри выбранном направлении движения по окружности имеется только три возможности для расположения ближайшего пикселя: на единицу вправо, на единицу вниз и по диагонали вниз (рис. 9.7). Выбор варианта можно осуществить, вычислив расстояния до этих точек и выбрав минимальное из них:

, , .

А

Рис. 9.7. Ближайший пиксель при

движении по окружности

лгоритм можно упростить, перейдя к анализу знаков величин . При диагональная точка лежит внутри окружности, поэтому ближайшими точками могут быть только диагональная и правая. Теперь достаточно проанализировать знак выражения . Если , выбираем горизонтальный шаг, в противном случае — диагональный. Если же , то определяем знак , и если , выбираем диагональный шаг, в противном случае — вертикальный. Затем вычисляется новое значение , причем желательно минимизировать вычисления не только этой величины, но и величин на каждом шаге алгоритма. Путем несложных преобразований можно получить для первого шага алгоритма, что .

После перехода точку по диагонали новое значение вычисляется по формуле , при горизонтальном переходе ( ) , при вертикальном — ( ) .

Таким образом, алгоритм рисования этой части окружности можно считать полностью описанным (блок-схема его приведена на рис. 9.8). Все оставшиеся ее части строятся параллельно: после получения очередной точки , можно инициализировать еще семь точек с координатами , , , , , , .

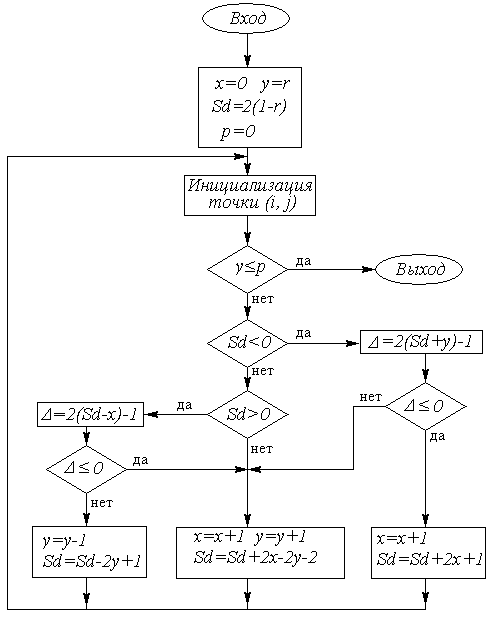
Рис. 9.8. Блок-схема построения восьмой части окружности

Для построения растровой развертки эллипса с осями, параллельными осям координат, и радиусами воспользуемся каноническим уравнением

,

которое перепишем в виде

.

В отличие от окружности, для которой было достаточно построить одну восьмую ее часть, а затем воспользоваться свойствами симметрии, эллипс имеет только две оси симметрии, поэтому придется строить одну четверть всей фигуры. За основу возьмем дугу, лежащую между точками и , лежащую в первом квадранте координатной плоскости. В каждой точке эллипса существует вектор нормали, задаваемый градиентом функции . Дугу разобьем на две части: первая — с углом между нормалью и горизонтальной осью больше 45⁰ (тангенс больше 1) и вторая — с углом, меньшим 45⁰ (рис. 9.9). Движение вдоль дуги будем осуществлять в направлении по часовой стрелке, начиная с точки . Вдоль всей дуги координата является монотонно убывающей функцией от , но в первой части она убывает медленнее, чем растет аргумент, а во второй быстрее. Поэтому при построении растрового образа в первой части будем увеличивать на единицу и искать соответствующее значение , а во второй сначала уменьшать значение на единицу и определять соответствующее значение .

Н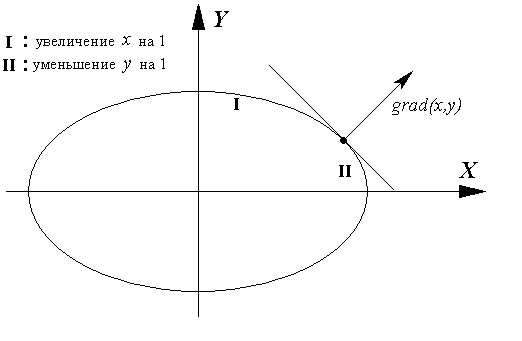 аправление нормали соответствует вектору

.

О

Рис. 9.9. Две области на участке эллипса

тсюда находим тангенс угла наклона вектора нормали: . Приравнивая его единице, получаем, что координаты точки деления дуги на вышеуказанные части удовлетворяют равенству . Поэтому критерием того, что мы переходим ко второй области в целочисленных координатах будет соотношение , или, переходя к целочисленным операциям, .

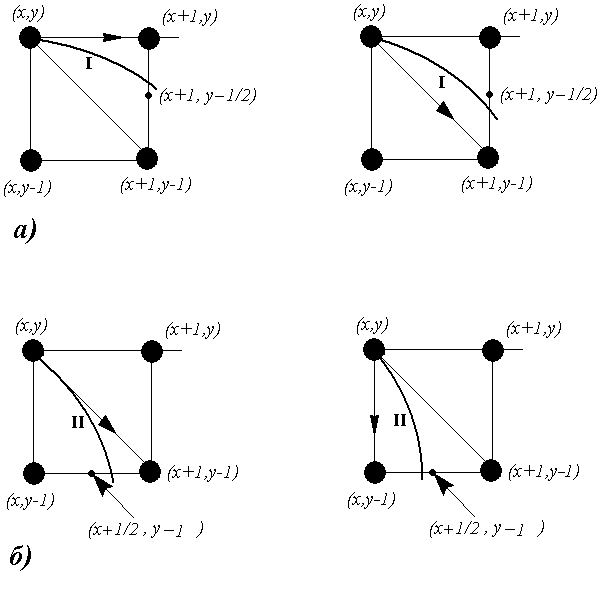
Рис. 9.10. Схема перехода в первой и второй областях дуги эллипса

При перемещении вдоль первого участка дуги мы из каждой точки переходим либо по горизонтали, либо по диагонали, и критерий такого перехода напоминает тот, который использовался при построении растрового образа окружности. Находясь в точке , мы будем вычислять значение . Если это значение меньше нуля, то дополнительная точка лежит внутри эллипса, следовательно, ближайшая точка растра есть , в противном случае это точка (рис. 9.10а).

На втором участке дуги возможен переход либо по диагонали, либо по вертикали, поэтому здесь сначала значение координаты y уменьшается на единицу, затем вычисляется и направление перехода выбирается аналогично предыдущему случаю (рис. 9.10б).

Остается оптимизировать вычисление параметра , умножив его на 4 и представив в виде функции координат точки. Тогда для первой половины дуги имеем

,

,

.

Для второй половины дуги получим

,

,

.

Все оставшиеся дуги эллипса строятся параллельно: после получения очередной точки , можно инициализировать еще три точки с координатами , , . Блок-схему алгоритма на приводим ввиду прозрачности алгоритма.