Матрицы
Для выполнения преобразований векторов
в пространстве мы будем использовать
матричный метод. Матрицей
размерности
называется таблица чисел вида
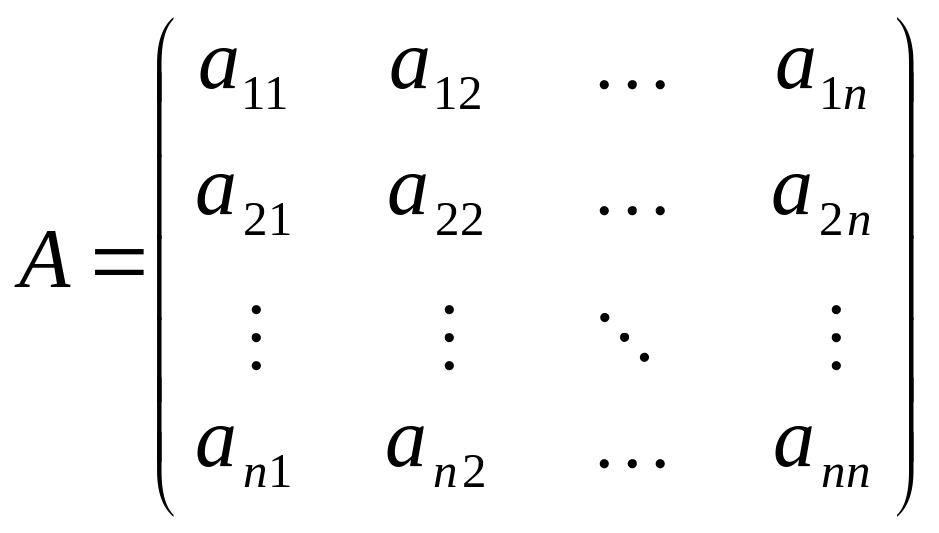
В дальнейшем будем использовать
сокращенную запись для матрицы:
.
Строки матрицы
будем называть вектор-строками
(поскольку каждая из них определяет
вектор), а столбцы
— вектор-столбцами.
Матрицы являются эффективным инструментом
для выполнения преобразований на
плоскости и в пространстве. В этих
случаях используются матрицы размерности
и
.
Сначала введем ряд операций над матрицами и векторами.
Пусть заданы матрицы
и
.
Суммой
матриц называется матрица
,
элементами которой являются
Определим также операцию умножения
матрицы на число. Результатом
умножения матрицы
на число
является матрица
,
элементы которой
.
Произведением двух матриц и называется матрица , элементы которой определяются следующим образом:
.
Произведение матриц некоммутативно,
т. е. в общем случае
.
Предыдущие определения мы вводили для
матриц произвольной размерности.
Следующие операции будут связаны с
векторами, и мы будем подразумевать,
что
или
.
Пусть задана матрица
и вектор
.
Результатом умножения матрицы на
вектор является вектор
,
координаты которого вычисляются как
скалярное произведение строки матрицы
на вектор:
.
Если матрица
получена из матрицы
путем замены всех вектор-строк на вектор
столбцы, т. е.
,
то ее называют транспонированной
матрицей
и обозначают
.
Аналогичным образом определяется умножение вектора на матрицу, только в этом случае вектор скалярно умножается на вектор-строки матрицы. Матрица вида
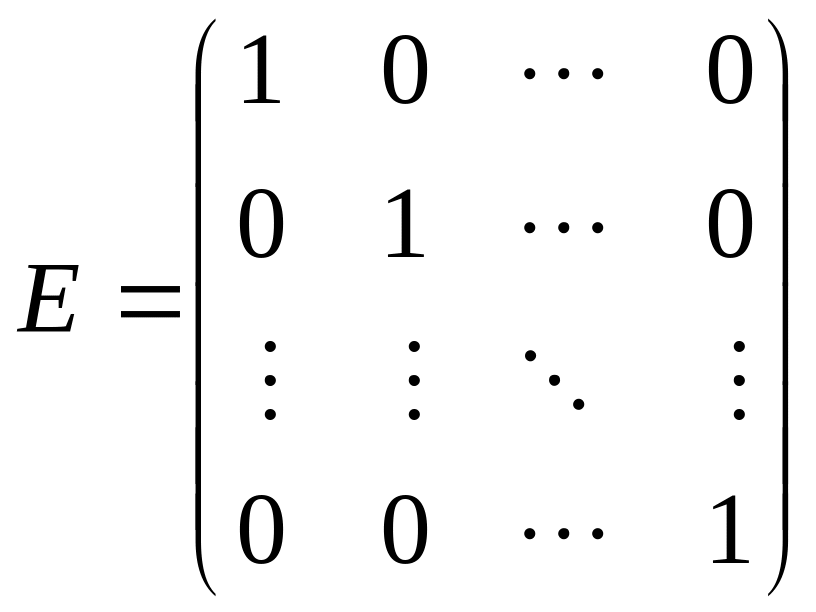
называется единичной, и обладает следующими свойствами:
—
для любой матрицы
.
—
для любого вектора
.
— Если для матрицы
существует матрица
,
такая, что
,
то
называется обратной матрицей к
и обозначается
.
При этом
и для любого вектора
получаем соотношения: если
,
то
.
— Если для матриц
и
существуют обратные матрицы, то существует
и обратная матрица для их произведения
и
.
Благодаря операции умножения матрицы на вектор любая матрица определяет преобразование в пространстве, по которому каждому вектору сопоставляется некоторый другой по вполне определенному закону.
Отметим, что для геометрических преобразований удобно использовать матрицы размерностью на единицу больше, чем размерность пространства, но об этом подробнее речь пойдет в следующей главе.
Геометрические преобразования (перенос, масштабирование, вращение)
Геометрические объекты на плоскости и в пространстве можно подвергать ряду различных преобразований. Наиболее употребительными в задачах компьютерной графики являются:
перемещение (параллельный перенос),
изменение размеров (масштабирование),
повороты вокруг некоторой точки на плоскости или некоторой оси в пространстве (вращение).
В дальнейшем мы часто будем отождествлять точки пространства с радиус-вектором, определяемым этой точкой.
Сначала рассмотрим преобразования на плоскости, или двумерные преобразования.
Параллельный перенос объекта сводится
к перемещению всех его точек на одно и
то же расстояние
в одном и том же направлении, заданном
определенным вектором 
.
Если этот вектор имеет длину
,
то операция переноса может быть
реализована путем сложения всех точек
объекта с вектором
.
Довольно просто доказать, что при такой
операции сохраняются расстояния между
точками и, как следствие, углы между
отрезками. Понятно также, что отрезки
прямых прейдут в отрезки прямых. Поэтому
при переносе многоугольника нет
необходимости подвергать этой операции
бесконечное множество точек, достаточно
просто перенести вершины, а затем
соединить их отрезками.
Масштабирование объекта можно реализовать
путем умножения координат всех его
точек на некоторое число. Пусть имеются
точки с координатами
и
,
над которыми выполняется такое
преобразование. Результатом будут новые
точки с координатами
и
.
Если
,
то несложно доказать, что обе точки
переместятся вдоль прямых, проходящих
через саму точку и начало координат,
т. е. в направлении своего же
радиус-вектора (рис. 3.5). При этом
расстояние между новыми точками будет
в
раз отличаться от прежнего, но углы
между отрезками сохранятся (это можно
показать, если выразить косинус угла
через скалярное произведение векторов).
Ясно, что если коэффициент масштабирования
больше единицы, соответствующий отрезок
растягивается, а если меньше, то сжимается.
Кроме того, при таком преобразовании
объект смещается.
В случае, когда
,
расстояния между точками изменятся
неравномерно, поскольку растяжения в
горизонтальном и вертикальном направлениях
будут различными. Углы между отрезками
также не сохранятся (рис. 3.6).
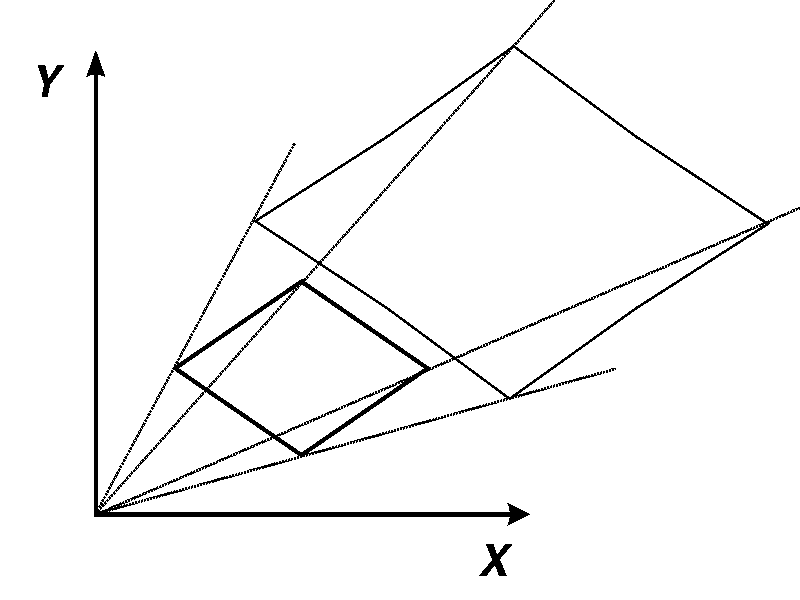
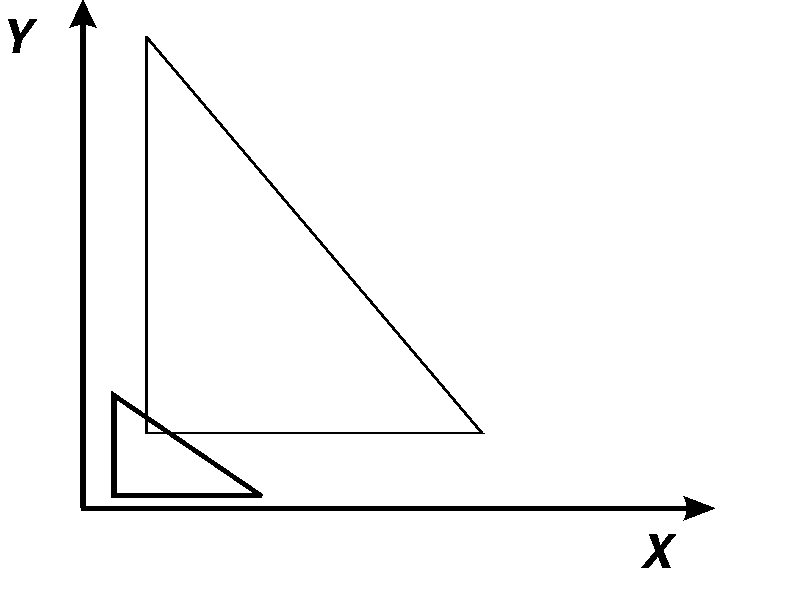
Рис. 3.5. Масштабирование с сохранением Рис. 3.6. Масштабирование с искажением
углов углов
Вращения в плоскости перемещают точки
по дуге окружности, центр которой
находится в начале координат. Рассмотрим
сначала движение одной точки при повороте
на угол
(положительным является направление
против часовой стрелки), т. е. поворот
радиус-вектора на угол (рис. 3.7). Пусть
точка располагалась на расстоянии
от начала координат, а ее радиус-вектор
составлял угол
с осью абсцисс. Тогда координаты точки
определяются формулами
.
После поворота вектор будет составлять
угол
,
а новые координаты точки будут определяться
соотношениями
.
(3.7)
Можно показать, что при таком преобразовании сохраняются расстояния между точками, а, следовательно, и углы между отрезками.
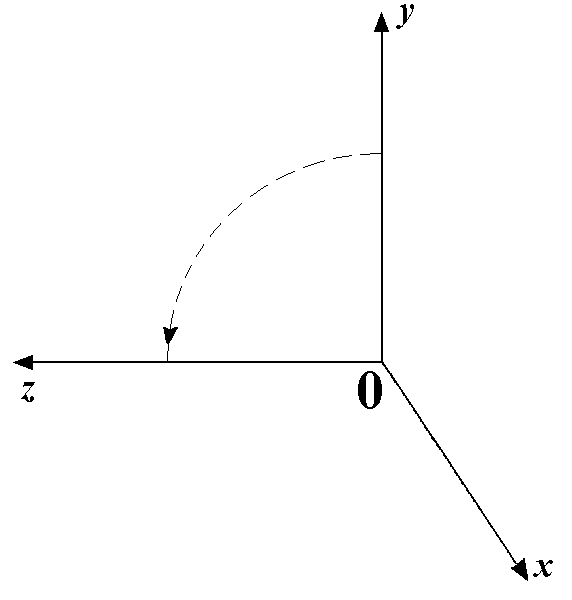
Рис. 3.7. Поворот на плоскости Рис. 3.8. Поворот в пространстве
В случае трехмерного пространства рассуждения, касающиеся переноса и масштабирования полностью аналогичны, только они распространяются на третью координату точек. С вращением же дело обстоит иначе, поскольку здесь вращательное движение есть перемещение вдоль поверхности сферы и поворот на какой-то угол относительно точки нельзя определить однозначно. Но перемещение из одной точки сферы в другую всегда можно осуществить последовательностью поворотов относительно осей координат, поэтому выведем формулы для этих трех вращений.
При повороте относительно оси OX на угол у всех точек координата x остается неизменной. Если смотреть на плоскость YOZ со стороны конца оси OX, то оси будут расположены так, как показано на рис. 3.8. Положительным считается поворот от оси OY к оси OZ. Если воспользоваться формулами для плоских поворотов, то координаты y' и z' новой точки определяются выражениями
Формулы поворота относительно оси OZ полностью совпадают с теми, которые были выведены для плоского случая, а поворот относительно оси OY выглядит так:
Во всех этих формулах следует обратить внимание на знаки, так как они зависят от того, какой поворот считается положительным (в данном случае мы имеем дело с правой тройкой базисных векторов).
Преобразования масштабирования и
поворота на плоскости и в пространстве
можно выразить с помощью матриц. Если
заданы коэффициенты масштабирования
,
то преобразование точки осуществляется
посредством умножения матрицы на ее
радиус-вектор,
.
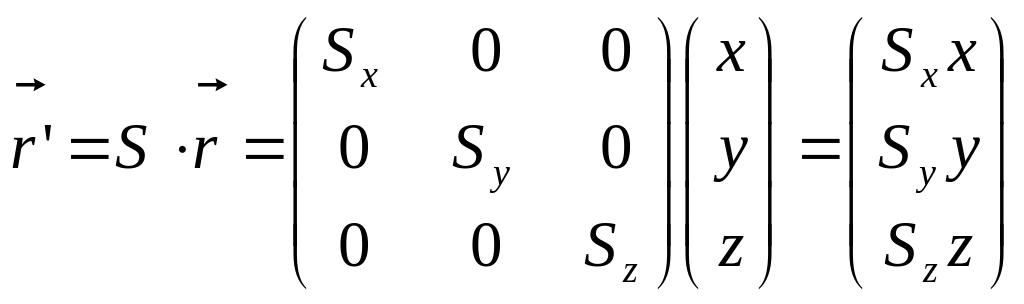(3.8)
Двумерный случай выглядит подобным же образом.
Поворот на плоскости можно осуществить с помощью матрицы
.
(3.9)
И, наконец, повороты в пространстве относительно осей координат можно выполнить с помощью трех матриц вращения
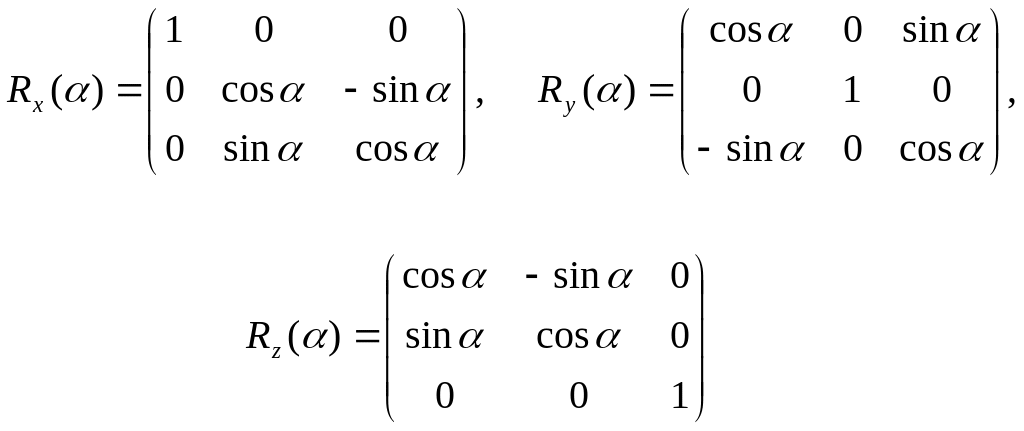. (3.10)
Нетрудно проверить, что для матриц вращения справедливо соотношение
.
Для выполнения последовательных
поворотов вокруг осей на углы
можно создать матрицу преобразования
путем перемножения трех матриц:
.
Использование этой матрицы даст заметную экономию в вычислениях по сравнению с последовательными умножениями на каждую из трех матриц вращения.