Переход в другую систему координат

Мы рассмотрели преобразования геометрических объектов, заданных в определенной декартовой системе координат. Но во многих случаях удобно рассматривать те же объекты в другой системе координат, поскольку их описание может стать более простым. Самый простой пример — задание координат параллелепипеда: проще всего это сделать в системе координат, совмещенной с одной из его вершин с осями, направленными вдоль ребер. В связи с этим остановимся на вопросе, как изменятся координаты точки при переходе от одной декартовой системы координат к другой.

П усть единичные орты первой системы координат обозначаются , а оси координат — OX, OY, OZ. Введем еще одну систему координат, единичные орты которой обозначим , а оси координат — O'X', O'Y', O'Z'. Эта система имеет свое начало координат и свои направления осей. Считаем, что в обеих системах координат орты образуют правую тройку (рис. 3.9).

Сначала рассмотрим ситуацию, когда точка O' совпадает с точкой O. Векторы можно задать в первой системе координат, разложив их по векторам :

Рис. 3.9. Две системы координат

в пространстве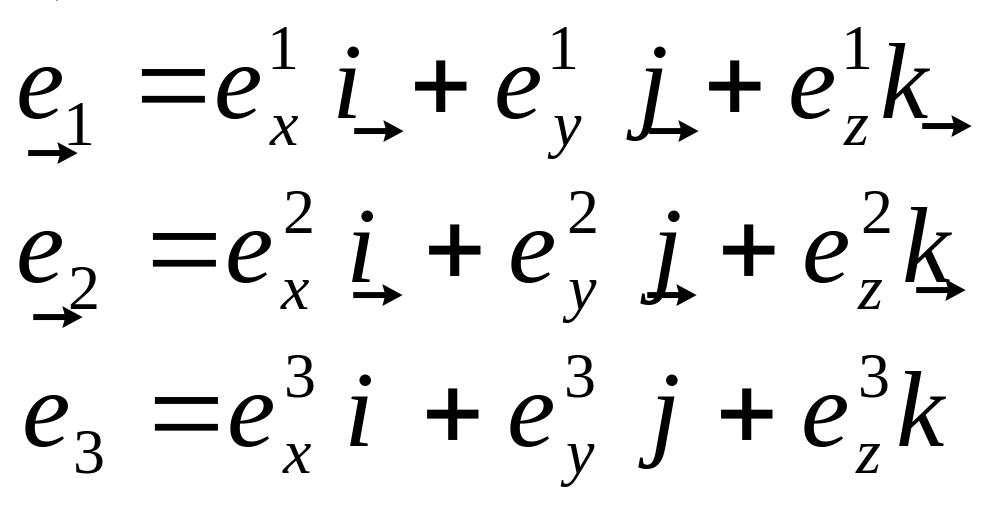

Если в первой системе точка имеет координаты , а во второй системе — , то, очевидно,

Умножая скалярно это соотношение на векторы , получим связь между значениями координат в разных системах:

Эти соотношения можно записать в матричном виде:

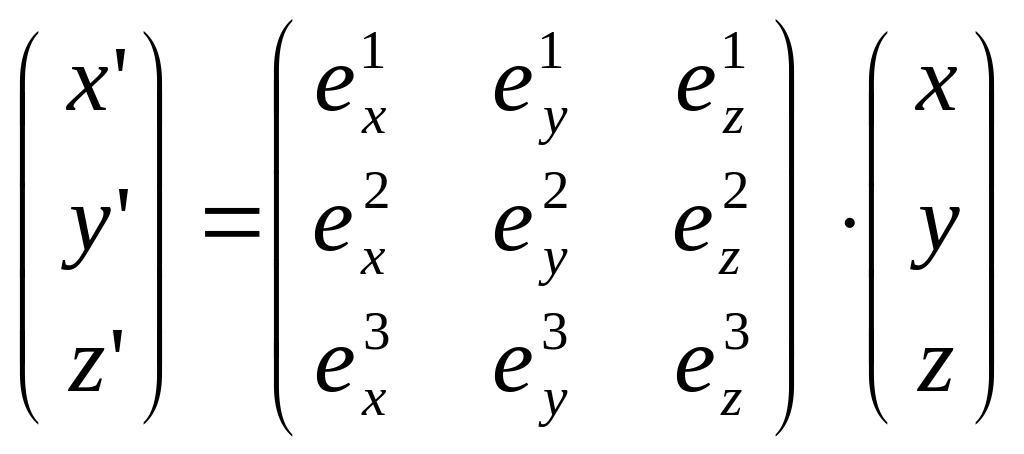, (3.11)

или в векторной записи

.

Предположим, что вторая система координат получена из первой путем поворота на угол относительно оси OY. Тогда

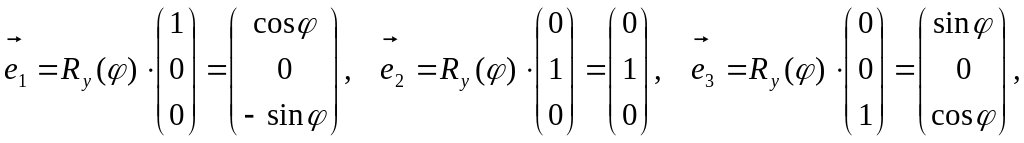
следовательно

.

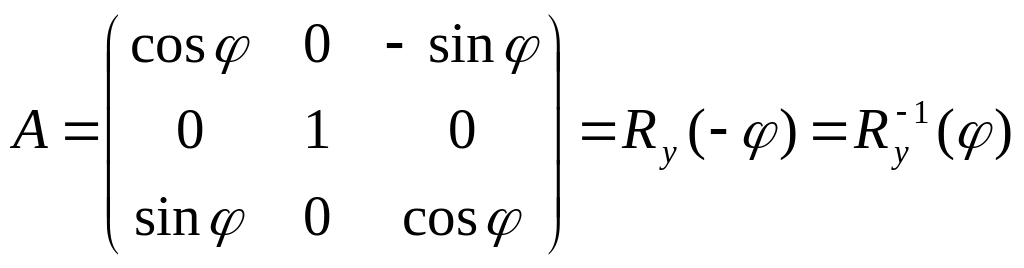Таким образом, при поворотах системы координат новые координаты точек получаются путем умножения матрицы поворота на противоположный угол на вектор исходных координат.

Если новая система координат получена из старой путем сдвига на вектор , то очевидно, что новые координаты точки задаются формулами

.

Теперь можно рассмотреть композицию двух преобразований системы координат — переноса и вращения. Тогда координаты точек преобразуются по формуле

(3.12)

Задача вращения относительно произвольной оси

Вращение относительно произвольной оси также можно реализовать посредством умножения матрицы на вектор, но предварительно эту матрицу надо построить. Предположим, что прямая проходит через начало координат и задана единичным вектором , и требуется выполнить поворот точки на угол относительно нее. Для этого воспользуемся следующим алгоритмом.

1. Совместим прямую с осью OZ посредством поворота системы координат относительно оси OX на угол , а затем поворота относительно оси OY на угол .

2. Выполним поворот относительно оси OZ на угол .

3. Выполним повороты системы сначала относительно оси OY на угол 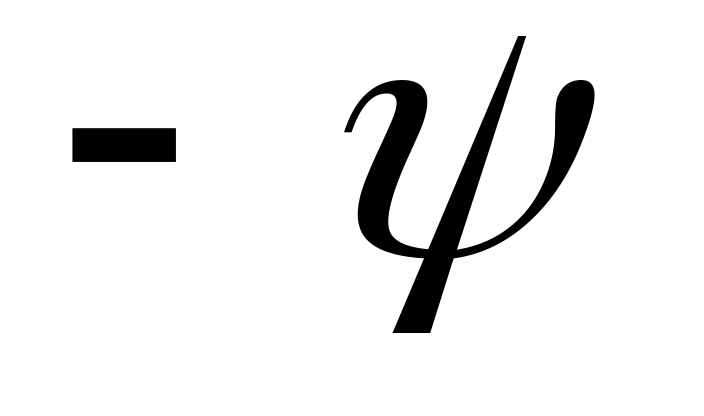, а затем относительно оси OX на угол (в обратном порядке по отношению к первым поворотам), тем самым возвращая ее в исходное положение.

Итоговая матрица преобразования таким образом является произведением нескольких матриц, а именно

Матрицы являются матрицами преобразования координат при поворотах системы координат, как было показано в предыдущем разделе. Определим сначала угол , который является углом между осью OZ и его проекцией вектора на плоскость YOZ . Пусть — длина этой проекции. Тогда , (синус отрицателен, поскольку поворот идет от оси OZ к оси OY, т. е. в отрицательном направлении). После поворота системы координат новыми координатами вектора будут . Угол — это угол между векторами и , поэтому , . Теперь мы можем выписать вид матриц преобразования координат для каждого шага алгоритма, учитывая то, что матрицы преобразования координат при повороте системы координат обратны по отношению соответствующим матрицам вращения.

Нетрудно убедиться, что последовательное умножение матриц и на вектор дадут в результате вектор , т. е. этот вектор действительно станет осью аппликат.

Остается только выписать окончательный вид матрицы (для сокращения записи введем следующие обозначения: , , ):

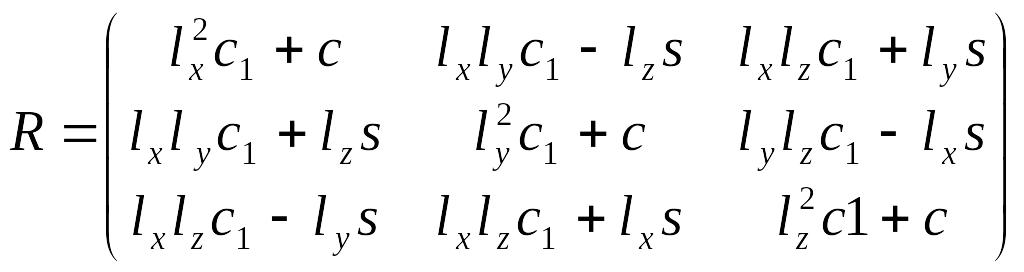. (3.13)

Напомним, что являются направляющими косинусами прямой, относительно которой выполняется поворот. Нетрудно убедиться, что если в качестве осей вращения взять оси координат, то мы в точности получим формулы (3.10).